8.2.1 不等式的解集 课件(共17张PPT) 华东师大版七年级数学下册
文档属性
| 名称 | 8.2.1 不等式的解集 课件(共17张PPT) 华东师大版七年级数学下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 171.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第八章 一元一次不等式
8.2 解一元一次不等式
第1课时 不等式的解集
学习导航
学习目标
合作探究
当堂检测
课堂总结
自主学习
新课导入
一、学习目标
1.理解不等式解集的概念,知道什么是解不等式;
2.会在数轴上表示不等式的解集,理解“数形结合”在不等式中的应用.(重点)
二、新课导入
上节课我们学习了不等式和不等式的解,你能写出不等式 x + 1 > 0 的几个解吗?
思考:如果要你写出该不等式的所有解,你该如何表示呢?
复习导入:
不等式 x + 1 > 0 的解:x = 0,1,2 等;
知识点1:不等式的解集与解不等式
三、自主学习
概念1:由上可知:0,1,2,3 … 都能使不等式 x + 1 > 0成立;
思考:不等式的解和解集有什么区别与联系呢?
所有这些解的全体称为这个不等式的解集;
求一个不等式的解集的过程称为解不等式;
一般地,能够使不等式成立的未知数的值,叫做这个不等式的解;
三、自主学习
总结:不等式的解与解集有什么区别与联系
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数
的某个值
满足一个不等式的未知数的所有值
个体
全体
x = 0.9 是 7 + 5x ≤ 12的一个解
x ≤ 1 是 7 + 5x ≤ 12 的 解集
某个解一定是解集中的一员
解集一定包括了某个解
知识点2:用数轴表示不等式的解集
三、自主学习
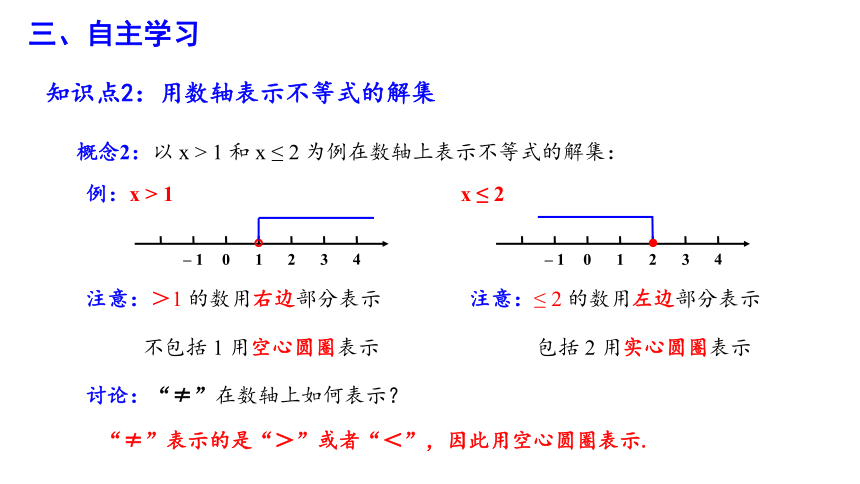
概念2:以 x > 1 和 x ≤ 2 为例在数轴上表示不等式的解集:
– 1
0
1
2
3
4
例:x > 1
– 1
0
1
2
3
4
x ≤ 2
注意:>1 的数用右边部分表示
不包括 1 用空心圆圈表示
注意:≤ 2 的数用左边部分表示
包括 2 用实心圆圈表示
讨论:“≠”在数轴上如何表示?
“≠”表示的是“>”或者“<”,因此用空心圆圈表示.
三、自主学习
总结:常用的几种不等号
小于
名称 符号 表示的意义 数轴上表示的点 数轴上表示的方向
大于号 > 左边大于右边 空心圆圈
小于号 < 左边 右边
大于或 等于号 ≥ 左边不小于右边
小于或 等于号 ≤ 左边 右边 实心圆点
空心圆圈
向左
向右
向左
向右
实心圆圈
不大于
四、合作探究
探究一:用数轴表示不等式的解集
问题探究:根据不等式的解在数轴上表示的方法可知:
(1) 不等式出现符号“ > ”,数轴上方向向 , (“能”或“不能”)取到 0 点;
活动1:在数轴上表示下列不等式的解集:
(1)x > 0; (2)x ≤ 3; (3) –1 < x ≤ 2; (4)x ≤ 2 且 x ≠ 1.
右
(2) 出现符号“ ”,方向向左,表示 的点是实心点;
(3)、(4) 可通过 分别进行分析,将不等式拆分成 ,取两段的 作为不等式的解集;
问题解决:(下接)
不能
≤
3
分段
两段
公共部分
问题解决:在数轴上表示下列不等式的解集:
(1)x > 0; (2)x ≤ 3; (3) –1 < x ≤ 2; (4)x ≤ 2 且 x ≠ 1.
(1)符号“ > ”,向右,空心:
– 1
0
1
2
3
4
(2)符号“ ≤ ”,向左,实心:
– 1
0
1
2
3
4
(3)分段:符号“ > ”,向右,空心;
– 1
0
1
2
3
4
符号“ ≤ ”,向左,实心:
四、合作探究
问题解决:在数轴上表示下列不等式的解集:(4)x ≤ 2 且 x ≠ 1;
(4)分段:符号“ ≤ ”,向左,实心;
– 1
0
1
2
3
4
总结:在数轴上表示不等式时:
(1)关键是根据符号判断在数轴上的方向,以及空心、实心;
(2)若有多个符号,可分段分析,最后取公共部分作为不等式的解集.
符号“ ≠ ”,空心:
四、合作探究
四、合作探究
练一练:
1. 在数轴上画出下列解集:x ≤ 2且 x ≠ 0.
解:x ≤ 2 且 x ≠ 0 在数轴上表示如上图:
– 1
0
1
2
3
4
四、合作探究
活动2 :观察下列解集在数轴上的表示方式.
问题探究:通过观察可知:
表示不等式的符号为“ ”;
(2)集合有 段,需要分段讨论;
右边的解集向左,点 3 是实心点,表示不等式的符号为“ ”;
问题提出:观察数轴,写出不等式的解集;
(1)数轴上集合向 ,且点 0 是 点;
左边的解集向右,点 – 1是空心点,表示不等式的符号为“ ”;
– 1
0
1
2
3
4
(1)
– 1
0
1
2
3
4
(2)
右
实心
≥
>
两
≤
问题解决:(下接)
四、合作探究
问题解决:
– 1
0
1
2
3
4
(1)
– 1
0
1
2
3
4
(2)
(1)向右,实心,不等式的解集为:x ≥ 0;
(2)分段:左边:方向向右,空心,解集为:x > –1;
右边:方向向左,实心,解集为:x ≤ 3;
故:该不等式的解集为:–1 < x ≤ 3;
注意:当数轴上存在多段解集时,要学会分段处理.
2. 观察下图,其中 x 所表示的解集正确的是( )
A. x ≥ 0 B. x ≠ 3
C. x ≥ 0 且 x ≠ 3 D. x > 0 且 x ≠ 3
– 1
0
1
2
3
4
四、合作探究
练一练:
D
–1
–4
0
1
2
3
4
5
6
7
–2
–3
描点:– 4,– 2,0,4.5 ,7 ;
1. 在数轴上表示不等式–3 ≤ x < 6的解集和 x 的下列值:– 4,– 2,0,4.5,7,并利用数轴说明 x 的这些数值中,哪些满足不等式– 3 ≤ x < 6,哪些不满足 .
解:–3 ≤ x < 6 在数轴上表示如下图:
根据上图可知:x 的下列值:– 2,0,4.5 满足不等式;
x 的下列值:– 4,7 不满足不等式.
五、当堂检测
不等式的解集
一个不等式所有解的集合,
叫这个不等式的解集;
在数轴上表示不等式的解集关键是:
① 方向:向左、向右;
② 取值:实心、空心 .
六、课堂总结
第八章 一元一次不等式
8.2 解一元一次不等式
第1课时 不等式的解集
学习导航
学习目标
合作探究
当堂检测
课堂总结
自主学习
新课导入
一、学习目标
1.理解不等式解集的概念,知道什么是解不等式;
2.会在数轴上表示不等式的解集,理解“数形结合”在不等式中的应用.(重点)
二、新课导入
上节课我们学习了不等式和不等式的解,你能写出不等式 x + 1 > 0 的几个解吗?
思考:如果要你写出该不等式的所有解,你该如何表示呢?
复习导入:
不等式 x + 1 > 0 的解:x = 0,1,2 等;
知识点1:不等式的解集与解不等式
三、自主学习
概念1:由上可知:0,1,2,3 … 都能使不等式 x + 1 > 0成立;
思考:不等式的解和解集有什么区别与联系呢?
所有这些解的全体称为这个不等式的解集;
求一个不等式的解集的过程称为解不等式;
一般地,能够使不等式成立的未知数的值,叫做这个不等式的解;
三、自主学习
总结:不等式的解与解集有什么区别与联系
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数
的某个值
满足一个不等式的未知数的所有值
个体
全体
x = 0.9 是 7 + 5x ≤ 12的一个解
x ≤ 1 是 7 + 5x ≤ 12 的 解集
某个解一定是解集中的一员
解集一定包括了某个解
知识点2:用数轴表示不等式的解集
三、自主学习
概念2:以 x > 1 和 x ≤ 2 为例在数轴上表示不等式的解集:
– 1
0
1
2
3
4
例:x > 1
– 1
0
1
2
3
4
x ≤ 2
注意:>1 的数用右边部分表示
不包括 1 用空心圆圈表示
注意:≤ 2 的数用左边部分表示
包括 2 用实心圆圈表示
讨论:“≠”在数轴上如何表示?
“≠”表示的是“>”或者“<”,因此用空心圆圈表示.
三、自主学习
总结:常用的几种不等号
小于
名称 符号 表示的意义 数轴上表示的点 数轴上表示的方向
大于号 > 左边大于右边 空心圆圈
小于号 < 左边 右边
大于或 等于号 ≥ 左边不小于右边
小于或 等于号 ≤ 左边 右边 实心圆点
空心圆圈
向左
向右
向左
向右
实心圆圈
不大于
四、合作探究
探究一:用数轴表示不等式的解集
问题探究:根据不等式的解在数轴上表示的方法可知:
(1) 不等式出现符号“ > ”,数轴上方向向 , (“能”或“不能”)取到 0 点;
活动1:在数轴上表示下列不等式的解集:
(1)x > 0; (2)x ≤ 3; (3) –1 < x ≤ 2; (4)x ≤ 2 且 x ≠ 1.
右
(2) 出现符号“ ”,方向向左,表示 的点是实心点;
(3)、(4) 可通过 分别进行分析,将不等式拆分成 ,取两段的 作为不等式的解集;
问题解决:(下接)
不能
≤
3
分段
两段
公共部分
问题解决:在数轴上表示下列不等式的解集:
(1)x > 0; (2)x ≤ 3; (3) –1 < x ≤ 2; (4)x ≤ 2 且 x ≠ 1.
(1)符号“ > ”,向右,空心:
– 1
0
1
2
3
4
(2)符号“ ≤ ”,向左,实心:
– 1
0
1
2
3
4
(3)分段:符号“ > ”,向右,空心;
– 1
0
1
2
3
4
符号“ ≤ ”,向左,实心:
四、合作探究
问题解决:在数轴上表示下列不等式的解集:(4)x ≤ 2 且 x ≠ 1;
(4)分段:符号“ ≤ ”,向左,实心;
– 1
0
1
2
3
4
总结:在数轴上表示不等式时:
(1)关键是根据符号判断在数轴上的方向,以及空心、实心;
(2)若有多个符号,可分段分析,最后取公共部分作为不等式的解集.
符号“ ≠ ”,空心:
四、合作探究
四、合作探究
练一练:
1. 在数轴上画出下列解集:x ≤ 2且 x ≠ 0.
解:x ≤ 2 且 x ≠ 0 在数轴上表示如上图:
– 1
0
1
2
3
4
四、合作探究
活动2 :观察下列解集在数轴上的表示方式.
问题探究:通过观察可知:
表示不等式的符号为“ ”;
(2)集合有 段,需要分段讨论;
右边的解集向左,点 3 是实心点,表示不等式的符号为“ ”;
问题提出:观察数轴,写出不等式的解集;
(1)数轴上集合向 ,且点 0 是 点;
左边的解集向右,点 – 1是空心点,表示不等式的符号为“ ”;
– 1
0
1
2
3
4
(1)
– 1
0
1
2
3
4
(2)
右
实心
≥
>
两
≤
问题解决:(下接)
四、合作探究
问题解决:
– 1
0
1
2
3
4
(1)
– 1
0
1
2
3
4
(2)
(1)向右,实心,不等式的解集为:x ≥ 0;
(2)分段:左边:方向向右,空心,解集为:x > –1;
右边:方向向左,实心,解集为:x ≤ 3;
故:该不等式的解集为:–1 < x ≤ 3;
注意:当数轴上存在多段解集时,要学会分段处理.
2. 观察下图,其中 x 所表示的解集正确的是( )
A. x ≥ 0 B. x ≠ 3
C. x ≥ 0 且 x ≠ 3 D. x > 0 且 x ≠ 3
– 1
0
1
2
3
4
四、合作探究
练一练:
D
–1
–4
0
1
2
3
4
5
6
7
–2
–3
描点:– 4,– 2,0,4.5 ,7 ;
1. 在数轴上表示不等式–3 ≤ x < 6的解集和 x 的下列值:– 4,– 2,0,4.5,7,并利用数轴说明 x 的这些数值中,哪些满足不等式– 3 ≤ x < 6,哪些不满足 .
解:–3 ≤ x < 6 在数轴上表示如下图:
根据上图可知:x 的下列值:– 2,0,4.5 满足不等式;
x 的下列值:– 4,7 不满足不等式.
五、当堂检测
不等式的解集
一个不等式所有解的集合,
叫这个不等式的解集;
在数轴上表示不等式的解集关键是:
① 方向:向左、向右;
② 取值:实心、空心 .
六、课堂总结
