华东师大版七年级数学下册8.2.2 不等式的简单变形课件(共20张PPT)
文档属性
| 名称 | 华东师大版七年级数学下册8.2.2 不等式的简单变形课件(共20张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 20:46:20 | ||
图片预览






文档简介
(共20张PPT)
第八章 一元一次不等式
8.2 解一元一次不等式
第2课时 不等式的简单变形
学习导航
学习目标
合作探究
当堂检测
课堂总结
自主学习
新课导入
一、学习目标
1.经历探索不等式性质的过程,掌握对不等式进行简单变形;
(重点)
2.会运用不等式的性质解简单的不等式;
二、新课导入
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法;你能通过等式的性质“类比”出不等式的性质吗?
思考:你能通过等式的性质推断出不等式的性质吗?
知识回顾:
三、合作探究
等式的性质1:如果 a = b,那么 a + c = b + c,a – c = b – c;
等式的性质2:如果 a = b,那么 ac = bc , (c ≠ 0).
探究一:从等式的性质 1 到不等式的性质 1
不等式的性质1:如果 a > b,那么 a + c > b + c,a – c > b – c;
等式的性质1:如果 a = b,那么 a + c = b + c,a – c = b – c;
即:不等式两边同时加上或减去同一个数,不等号方向不变.
设计活动:运用天平验证不等式的性质 1 ;
三、合作探究
提出猜想:
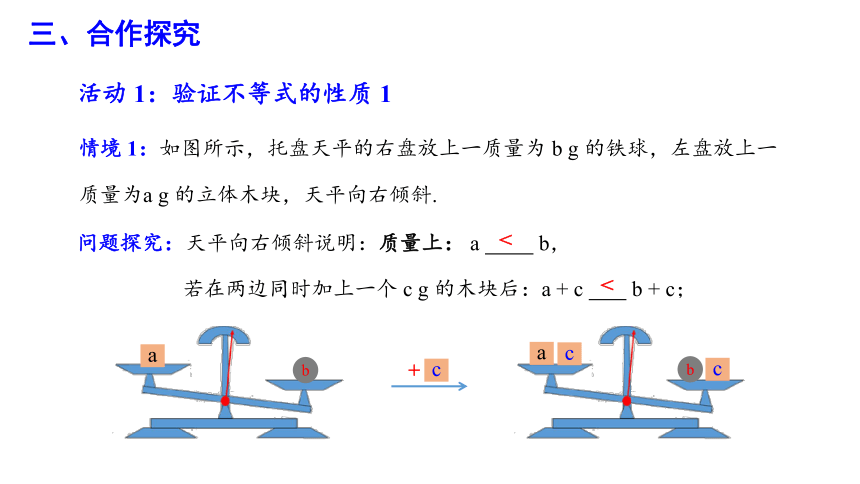
活动 1:验证不等式的性质 1
a
b
情境 1:如图所示,托盘天平的右盘放上一质量为 b g 的铁球,左盘放上一质量为a g 的立体木块,天平向右倾斜.
问题探究:天平向右倾斜说明:质量上: a b,
若在两边同时加上一个 c g 的木块后:a + c b + c;
<
<
a
b
c
c
+ c
c
三、合作探究
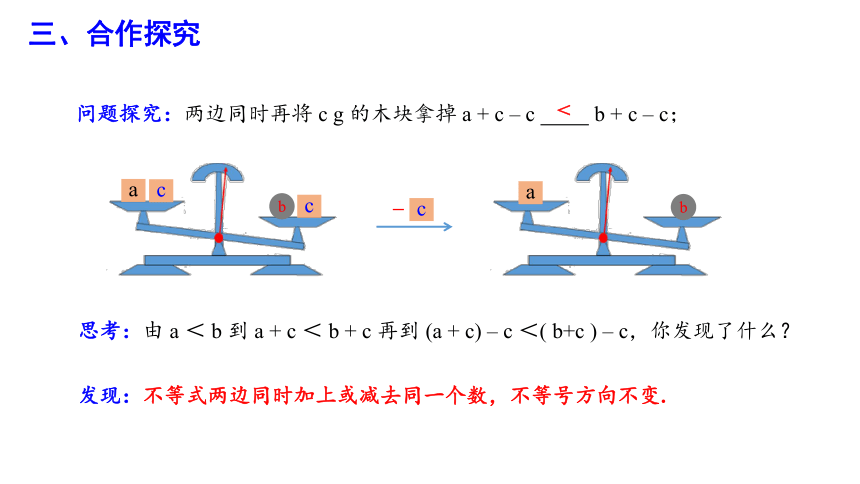
思考:由 a < b 到 a + c < b + c 再到 (a + c) – c <( b+c ) – c,你发现了什么?
三、合作探究
问题探究:两边同时再将 c g 的木块拿掉 a + c – c b + c – c;
<
a
b
a
b
c
c
– c
c
发现:不等式两边同时加上或减去同一个数,不等号方向不变.
即:如果 a > b,那么 a + c > b + c,且 a – c > b – c .
三、合作探究
总结:不等式的性质 1
不等式两边都加上(或都减去)同一个数或同一个整式,不等号的方向不变.
探究二:从等式的性质 2 到不等式的性质 2
即:不等式两边同时乘以或除以同一个数(除数大于0),不等号方向不变.
设计活动:运用天平验证不等式的性质 2 ;
三、合作探究
提出猜想:
等式的性质2:如果 a = b,那么 ac = bc , (c ≠ 0).
不等式的性质 2 :如果 a > b,那么 ac > bc, (c > 0) ;
活动 2:验证不等式的性质 2
情境 2:如图所示,托盘天平的右盘放上两个质量为 b g 的铁球,左盘放上两个质量为 a g 的立体木块,天平向右倾斜.
问题探究:天平向右倾斜说明:质量上: 2a 2b,
两边重量同时扩大 2 倍后:2a × 2 2b × 2;
<
<
× 2
三、合作探究
a
b
a
b
a
b
a
a
a
b
b
b
思考:由2a < 2b到 2a×2 < 2b×2 再到 2a÷2 < 2b÷2,你发现了什么?
三、合作探究
问题探究:如果一开始两边重量同时减少一半:2a ÷2 2b ÷2;
<
a
b
÷ 2
发现:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
a
b
a
b
三、合作探究
总结:不等式的性质 2
不等式两边都乘以(或除以)同一个正数,不等号的方向不变.
即:如果 a > b,并且 c > 0 ,那么 ac > bc,且 .
思考:若上述结论中的 c < 0,结论还成立吗?
即:如果 a > b,并且 c < 0 ,那么 ac > bc,且 .
问题探究:通过分类讨论得:
显然 – a < – b;
问题 1:观察数轴,如果 a > b,那么它们的相反数 – a与– b 哪个大,你能用数轴上点的位置关系加以说明吗?
① 如果 a ≥ 0,b ≤ 0 ( a 和 b 不同时为0 ):那么 –a 0,–b 0;
b
a
三、合作探究
活动3 :验证猜想:
如果 a > b,并且 c < 0 ,那么 ac > bc,且 .
≤
≥
② 如果 a > 0,b ≥ 0:那么 a 比 b 离原点远 ;同样 – a 也比 – b 离原点更远;– a 位于原点 侧,而且离原点更远,所以 –a –b;
左
<
③ 如果 a ≤ 0,b < 0:我们同样可推出 – a < – b .
总结:我们得出如果 a > b ,则 – a < – b.
三、合作探究
问题2:如果 a > b,那么 –a < –b,这个式子可理解为:
a× < b× ;
–1
–1
思考:这样,对于不等式 a > b,两边同时乘以 – 3,会得到什么结果呢?
由 a > b可得 – a <– b,由不等式的性质2可得:–a×3 –b×3;
<
因为 –a×3 = a×(–3),–b×3 = b×(–3),所以我们得到: ;
a×(–3) < b×(–3)
结论:如果a > b,c < 0,那么 ac 与 bc 有这样的关系: ;
ac < bc
猜想错误!
三、合作探究
总结:不等式的性质 3
不等式两边都乘以(或除以)同一个负数,不等号的方向改变.
即:如果 a > b,并且 c < 0 ,那么 ac < bc,且 .
易错点:
c > 0,那么 ac > bc,且 .
c < 0 ,那么 ac < bc,且 .
如果 a > b
–1
0
1
2
3
4
5
1. 运用不等式的性质下列解不等式,并把解集在数轴上表示出来:
(1)x – 3 < 1; (2)3x ≥ 6; (3)–2x > 4;
分析:(1)运用不等式的性质 1 解答即可:
五、当堂检测
解:(1)两边同时 + 3 得:x – 3 + 3 < 1 + 3;
即:x < 4;
向左,空心:
注:这里的不等式变形类似与方程的变形中的“移项”.
–1
0
1
2
3
4
5
(2)3x ≥ 6; (3)–2x > 4;
分析:(2)运用不等式的性质 2 解答即可:
五、当堂检测
解:(2)两边同时 除以 3 得:3x ÷ 3 ≥ 6 ÷ 3;
即:x ≥ 2;
向右,实心:
注:这里的不等式变形类似与方程的变形中的“将未知数系数化为 1 ”.
–5
-4
-3
-2
-1
0
1
(3)–2x > 4;
分析:(3)运用不等式的性质 3 解答即可:
五、当堂检测
解:(3)两边同时 除以 – 2 得:–2x ÷ –2 < 4 ÷ –2 (变号) ;
即:x < –2;
向左,空心:
注:不等式两边同时乘以(或除以)一个负数,不等号的方向改变.
六、课堂总结
第八章 一元一次不等式
8.2 解一元一次不等式
第2课时 不等式的简单变形
学习导航
学习目标
合作探究
当堂检测
课堂总结
自主学习
新课导入
一、学习目标
1.经历探索不等式性质的过程,掌握对不等式进行简单变形;
(重点)
2.会运用不等式的性质解简单的不等式;
二、新课导入
有一次,鲁班的手不慎被一片小草叶子割破了,他发现小草叶子的边缘布满了密集的小齿,于是便产生联想,根据小草的结构发明了锯子.
鲁班在这里就运用了“类比”的思想方法;你能通过等式的性质“类比”出不等式的性质吗?
思考:你能通过等式的性质推断出不等式的性质吗?
知识回顾:
三、合作探究
等式的性质1:如果 a = b,那么 a + c = b + c,a – c = b – c;
等式的性质2:如果 a = b,那么 ac = bc , (c ≠ 0).
探究一:从等式的性质 1 到不等式的性质 1
不等式的性质1:如果 a > b,那么 a + c > b + c,a – c > b – c;
等式的性质1:如果 a = b,那么 a + c = b + c,a – c = b – c;
即:不等式两边同时加上或减去同一个数,不等号方向不变.
设计活动:运用天平验证不等式的性质 1 ;
三、合作探究
提出猜想:
活动 1:验证不等式的性质 1
a
b
情境 1:如图所示,托盘天平的右盘放上一质量为 b g 的铁球,左盘放上一质量为a g 的立体木块,天平向右倾斜.
问题探究:天平向右倾斜说明:质量上: a b,
若在两边同时加上一个 c g 的木块后:a + c b + c;
<
<
a
b
c
c
+ c
c
三、合作探究
思考:由 a < b 到 a + c < b + c 再到 (a + c) – c <( b+c ) – c,你发现了什么?
三、合作探究
问题探究:两边同时再将 c g 的木块拿掉 a + c – c b + c – c;
<
a
b
a
b
c
c
– c
c
发现:不等式两边同时加上或减去同一个数,不等号方向不变.
即:如果 a > b,那么 a + c > b + c,且 a – c > b – c .
三、合作探究
总结:不等式的性质 1
不等式两边都加上(或都减去)同一个数或同一个整式,不等号的方向不变.
探究二:从等式的性质 2 到不等式的性质 2
即:不等式两边同时乘以或除以同一个数(除数大于0),不等号方向不变.
设计活动:运用天平验证不等式的性质 2 ;
三、合作探究
提出猜想:
等式的性质2:如果 a = b,那么 ac = bc , (c ≠ 0).
不等式的性质 2 :如果 a > b,那么 ac > bc, (c > 0) ;
活动 2:验证不等式的性质 2
情境 2:如图所示,托盘天平的右盘放上两个质量为 b g 的铁球,左盘放上两个质量为 a g 的立体木块,天平向右倾斜.
问题探究:天平向右倾斜说明:质量上: 2a 2b,
两边重量同时扩大 2 倍后:2a × 2 2b × 2;
<
<
× 2
三、合作探究
a
b
a
b
a
b
a
a
a
b
b
b
思考:由2a < 2b到 2a×2 < 2b×2 再到 2a÷2 < 2b÷2,你发现了什么?
三、合作探究
问题探究:如果一开始两边重量同时减少一半:2a ÷2 2b ÷2;
<
a
b
÷ 2
发现:不等式的两边都乘以(或除以)同一个正数,不等号的方向不变.
a
b
a
b
三、合作探究
总结:不等式的性质 2
不等式两边都乘以(或除以)同一个正数,不等号的方向不变.
即:如果 a > b,并且 c > 0 ,那么 ac > bc,且 .
思考:若上述结论中的 c < 0,结论还成立吗?
即:如果 a > b,并且 c < 0 ,那么 ac > bc,且 .
问题探究:通过分类讨论得:
显然 – a < – b;
问题 1:观察数轴,如果 a > b,那么它们的相反数 – a与– b 哪个大,你能用数轴上点的位置关系加以说明吗?
① 如果 a ≥ 0,b ≤ 0 ( a 和 b 不同时为0 ):那么 –a 0,–b 0;
b
a
三、合作探究
活动3 :验证猜想:
如果 a > b,并且 c < 0 ,那么 ac > bc,且 .
≤
≥
② 如果 a > 0,b ≥ 0:那么 a 比 b 离原点远 ;同样 – a 也比 – b 离原点更远;– a 位于原点 侧,而且离原点更远,所以 –a –b;
左
<
③ 如果 a ≤ 0,b < 0:我们同样可推出 – a < – b .
总结:我们得出如果 a > b ,则 – a < – b.
三、合作探究
问题2:如果 a > b,那么 –a < –b,这个式子可理解为:
a× < b× ;
–1
–1
思考:这样,对于不等式 a > b,两边同时乘以 – 3,会得到什么结果呢?
由 a > b可得 – a <– b,由不等式的性质2可得:–a×3 –b×3;
<
因为 –a×3 = a×(–3),–b×3 = b×(–3),所以我们得到: ;
a×(–3) < b×(–3)
结论:如果a > b,c < 0,那么 ac 与 bc 有这样的关系: ;
ac < bc
猜想错误!
三、合作探究
总结:不等式的性质 3
不等式两边都乘以(或除以)同一个负数,不等号的方向改变.
即:如果 a > b,并且 c < 0 ,那么 ac < bc,且 .
易错点:
c > 0,那么 ac > bc,且 .
c < 0 ,那么 ac < bc,且 .
如果 a > b
–1
0
1
2
3
4
5
1. 运用不等式的性质下列解不等式,并把解集在数轴上表示出来:
(1)x – 3 < 1; (2)3x ≥ 6; (3)–2x > 4;
分析:(1)运用不等式的性质 1 解答即可:
五、当堂检测
解:(1)两边同时 + 3 得:x – 3 + 3 < 1 + 3;
即:x < 4;
向左,空心:
注:这里的不等式变形类似与方程的变形中的“移项”.
–1
0
1
2
3
4
5
(2)3x ≥ 6; (3)–2x > 4;
分析:(2)运用不等式的性质 2 解答即可:
五、当堂检测
解:(2)两边同时 除以 3 得:3x ÷ 3 ≥ 6 ÷ 3;
即:x ≥ 2;
向右,实心:
注:这里的不等式变形类似与方程的变形中的“将未知数系数化为 1 ”.
–5
-4
-3
-2
-1
0
1
(3)–2x > 4;
分析:(3)运用不等式的性质 3 解答即可:
五、当堂检测
解:(3)两边同时 除以 – 2 得:–2x ÷ –2 < 4 ÷ –2 (变号) ;
即:x < –2;
向左,空心:
注:不等式两边同时乘以(或除以)一个负数,不等号的方向改变.
六、课堂总结
