6.1 平方根 第2课时 课件 2023-2024学年初中数学人教版七年级下册(18张PPT)
文档属性
| 名称 | 6.1 平方根 第2课时 课件 2023-2024学年初中数学人教版七年级下册(18张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 782.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 08:00:10 | ||
图片预览






文档简介
(共18张PPT)
6.1 平方根
第六章 实数
第2课时
一、学习目标
1.能说出平方根的概念,知道平方根的特点,会用根号表示平方根.
2.知道开平方与平方互为逆运算,会用平方运算或计算器求某些非负数的平方根.
二、新课导入
(1)4的算术平方根是多少?
因为22=4, 所以4的算术平方根是2;
(2)0.81的算术平方根是多少?
因为0.92=0.81, 所以0.81的算术平方根是0.9;
(3)0的算术平方根是多少?
0 的算术平方根是0;
旧知回顾
三、概念剖析
(一)平方根
1.如果一个数的平方等于9,这个数是多少?
从上节课我们可以知道,9的算术平方根是3.
2.除了3以外,还有没有别的数字的平方也等于9呢?
思考:
由于(-3)2=9,这个数也可以是-3.
三、概念剖析
想一想:你能从表格中发现什么吗?
填表:
±1
±4
±7
±6
x2 1 16 36 49
x
如果一个数的平方等于x2,那么这个数是x或-x.
三、概念剖析
一般地,如果一个数的平方等于a,那么这个正数 x 叫做 a 的平方根或二次方根,这就是说,如果x2=a,那么x叫做a的平方根.
求一个数a 的平方根的运算,叫做开平方.
新知
三、概念剖析
+1
-1
+2
-2
+3
-3
+1
-1
+2
-2
+3
-3
1
4
9
1
4
9
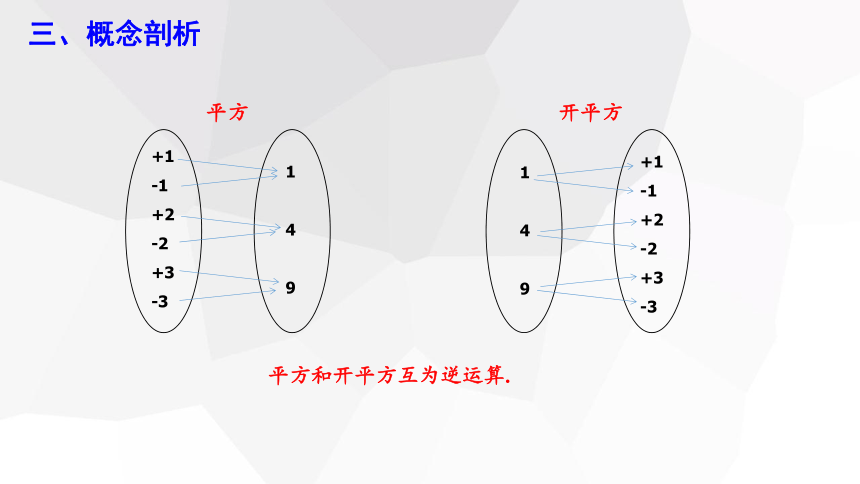
平方
开平方
平方和开平方互为逆运算.
三、概念剖析
(二)平方根的性质
议一议
(1)一个正数有几个平方根?
一个正数有两个平方根;它们互为相反数,正数a的算术平方根可以用 表示,正数a的负的平方根,可以用符号“ ” 表示,故正数a的平方根可以用“ ”表示,读作“正、负根号a”
例如:(±4)2=16,则+4和-4都是16的平方根;
即16的平方根是±4; +4是16的算术平方根.
三、概念剖析
(2)0 有几个平方根?
0只有一个平方根,它是0本身;即 ;
(3)负数呢?
负数没有平方根.
归纳总结
正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
四、典型例题
例1:求下列各数的平方根:
(1) 64; (2) ; (3)100; (4) ;(5)11.
解: (1)因为(±8)2=64, 所以64的平方根是±8,即 ;
(2)因为 , 所以 的平方根是 ,即 ;
提示:因为平方和开平方为互逆运算,根据这种互逆关系,可以求一个数的平方根.
四、典型例题
(3)因为(±10)2=100,所以100的平方根是±10;
(4)因为 ,所以 的平方根是 ;
(5)11的平方根是 .
例1:求下列各数的平方根:
(1) 64; (2) ; (3)100; (4) ;(5)11.
【当堂检测】
1.下列说法错误的是( )
A.0的平方根是0 B.4的平方根是±2
C.-16的平方根是±4 D.2是4的平方根
C
【当堂检测】
2.求下列各数的平方根.
(1)100;(2)(-25)2 ;(3)0.25
(1)因为 (±0.02)2=0.0004,所以0.0004的平方根是0.02,即 ;
(2)因为(±25)2=(-25)2, 所以(-25)2的平方根是±25,即 ;
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
四、典型例题
例2:求下列各式的值.
(1) ; (2) ; (3) ;(4) ;
解:(1)因为252=625,所以 ;
(2)因为 , ,所以 ;
(3)因为 , ,所以 ;
(4)因为(-2)2=4,22=4,所以 ;
归纳总结
解决此类问题的关键是弄清楚 、 、 、三者所表示的含义.
表示a的算术平方根,
表示a的算术平方根的相反数,
表示a的平方根.
四、典型例题
【当堂检测】
3.下列各数13,π,0,-4,(-3)2,-32,-|-3|,-(-3),3.14-π中有平方根的个数为( )
A.3 B.4 C.5 D.6
D
【当堂检测】
4.求下列各式的值.
(1)- ;(2) ;(3)±
解:(1)因为32=9,所以 ;
(2)因为 ,所以 ;
(3)因为0.52=0.25,所以 ;
五、课堂总结
一般地,如果一个数的平方等于a,那么这个正数 x 叫做 a 的平方根或二次方根,这就是说,如果x2=a,那么x叫做a的平方根.
求一个数a 的平方根的运算,叫做开平方.
正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
6.1 平方根
第六章 实数
第2课时
一、学习目标
1.能说出平方根的概念,知道平方根的特点,会用根号表示平方根.
2.知道开平方与平方互为逆运算,会用平方运算或计算器求某些非负数的平方根.
二、新课导入
(1)4的算术平方根是多少?
因为22=4, 所以4的算术平方根是2;
(2)0.81的算术平方根是多少?
因为0.92=0.81, 所以0.81的算术平方根是0.9;
(3)0的算术平方根是多少?
0 的算术平方根是0;
旧知回顾
三、概念剖析
(一)平方根
1.如果一个数的平方等于9,这个数是多少?
从上节课我们可以知道,9的算术平方根是3.
2.除了3以外,还有没有别的数字的平方也等于9呢?
思考:
由于(-3)2=9,这个数也可以是-3.
三、概念剖析
想一想:你能从表格中发现什么吗?
填表:
±1
±4
±7
±6
x2 1 16 36 49
x
如果一个数的平方等于x2,那么这个数是x或-x.
三、概念剖析
一般地,如果一个数的平方等于a,那么这个正数 x 叫做 a 的平方根或二次方根,这就是说,如果x2=a,那么x叫做a的平方根.
求一个数a 的平方根的运算,叫做开平方.
新知
三、概念剖析
+1
-1
+2
-2
+3
-3
+1
-1
+2
-2
+3
-3
1
4
9
1
4
9
平方
开平方
平方和开平方互为逆运算.
三、概念剖析
(二)平方根的性质
议一议
(1)一个正数有几个平方根?
一个正数有两个平方根;它们互为相反数,正数a的算术平方根可以用 表示,正数a的负的平方根,可以用符号“ ” 表示,故正数a的平方根可以用“ ”表示,读作“正、负根号a”
例如:(±4)2=16,则+4和-4都是16的平方根;
即16的平方根是±4; +4是16的算术平方根.
三、概念剖析
(2)0 有几个平方根?
0只有一个平方根,它是0本身;即 ;
(3)负数呢?
负数没有平方根.
归纳总结
正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
四、典型例题
例1:求下列各数的平方根:
(1) 64; (2) ; (3)100; (4) ;(5)11.
解: (1)因为(±8)2=64, 所以64的平方根是±8,即 ;
(2)因为 , 所以 的平方根是 ,即 ;
提示:因为平方和开平方为互逆运算,根据这种互逆关系,可以求一个数的平方根.
四、典型例题
(3)因为(±10)2=100,所以100的平方根是±10;
(4)因为 ,所以 的平方根是 ;
(5)11的平方根是 .
例1:求下列各数的平方根:
(1) 64; (2) ; (3)100; (4) ;(5)11.
【当堂检测】
1.下列说法错误的是( )
A.0的平方根是0 B.4的平方根是±2
C.-16的平方根是±4 D.2是4的平方根
C
【当堂检测】
2.求下列各数的平方根.
(1)100;(2)(-25)2 ;(3)0.25
(1)因为 (±0.02)2=0.0004,所以0.0004的平方根是0.02,即 ;
(2)因为(±25)2=(-25)2, 所以(-25)2的平方根是±25,即 ;
(3)因为(±0.5)2=0.25,所以0.25的平方根是±0.5.
四、典型例题
例2:求下列各式的值.
(1) ; (2) ; (3) ;(4) ;
解:(1)因为252=625,所以 ;
(2)因为 , ,所以 ;
(3)因为 , ,所以 ;
(4)因为(-2)2=4,22=4,所以 ;
归纳总结
解决此类问题的关键是弄清楚 、 、 、三者所表示的含义.
表示a的算术平方根,
表示a的算术平方根的相反数,
表示a的平方根.
四、典型例题
【当堂检测】
3.下列各数13,π,0,-4,(-3)2,-32,-|-3|,-(-3),3.14-π中有平方根的个数为( )
A.3 B.4 C.5 D.6
D
【当堂检测】
4.求下列各式的值.
(1)- ;(2) ;(3)±
解:(1)因为32=9,所以 ;
(2)因为 ,所以 ;
(3)因为0.52=0.25,所以 ;
五、课堂总结
一般地,如果一个数的平方等于a,那么这个正数 x 叫做 a 的平方根或二次方根,这就是说,如果x2=a,那么x叫做a的平方根.
求一个数a 的平方根的运算,叫做开平方.
正数有两个平方根,它们互为相反数;0的平方根是0;负数没有平方根.
