6.3 实数 第1课时 课件 2023-2024学年初中数学人教版七年级下册(20张PPT)
文档属性
| 名称 | 6.3 实数 第1课时 课件 2023-2024学年初中数学人教版七年级下册(20张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1002.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 00:00:00 | ||
图片预览







文档简介
(共20张PPT)
6.3 实数
第六章 实数
第1课时
一、学习目标
1.能说出无理数和实数的概念,会对实数按一定的标准进行分类.
2.能说明实数和数轴上的点是一一对应的,渗透“数形结合”的思想.
毕德哥拉斯
古希腊著名的数学家毕达哥拉斯曾说过这样的一句话:“世界上只有整数和分数,除此之外就再也没有什么别的数了!”
同学们,你们赞成这位数学家的说法吗
二、新课导入
我们发现,上面的分数都可以写成有限小数或者无限循环小数的形式,即:
我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
(一)实数的分类
三、概念剖析
事实上,如果把整数看成小数点后是0的小数,那么任何一个有理数可以写成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
新知
三、概念剖析
通过平方根的学习,我们可以知道:
像有理数一样,无理数也有正负之分,例如:
, ,π都是正无理数;
, ,-π都是负无理数;
无限不循环小数:小数位数无限,且小数部分不循环的小数.
无限不循环小数又叫做无理数.
三、概念剖析
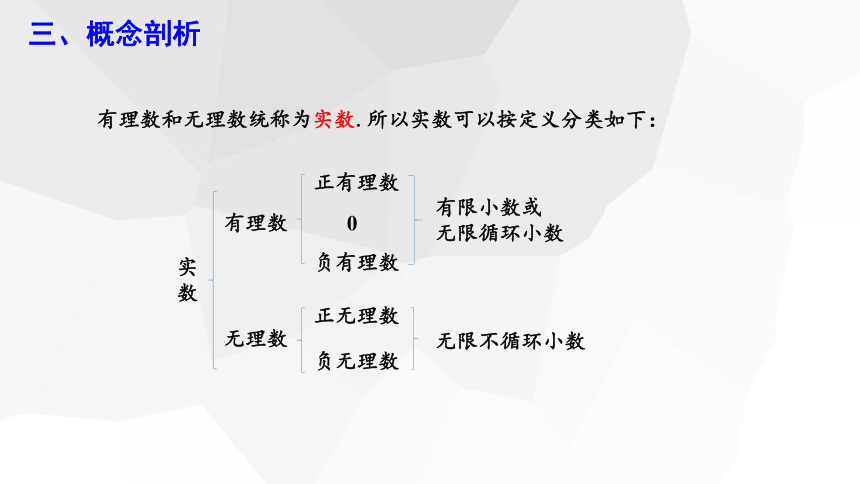
有理数和无理数统称为实数.所以实数可以按定义分类如下:
有限小数或
无限循环小数
正有理数
有理数
实数
无理数
负有理数
0
正无理数
负无理数
无限不循环小数
三、概念剖析
由于非0有理数和无理数都有正负之分,实数也有正负之分,所以实数还可以按大小分类如下:
实数
0
正实数
负实数
正有理数
正无理数
负有理数
负无理数
三、概念剖析
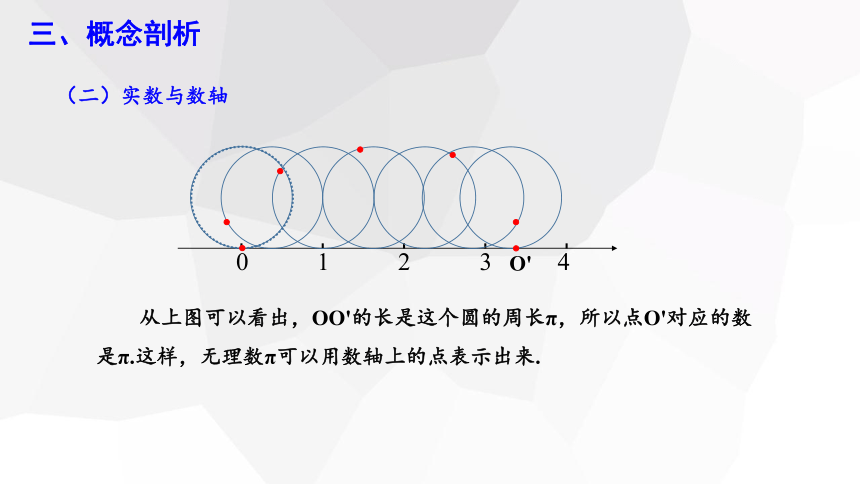
(二)实数与数轴
0
1
3
2
4
O'
从上图可以看出,OO'的长是这个圆的周长π,所以点O'对应的数是π.这样,无理数π可以用数轴上的点表示出来.
三、概念剖析
0
-2
-1
1
3
2
如上图,以单位长度为边长画一个正方形,
以原点为圆心,正方形的对角线长为半径画弧,
与正半轴的交点就表示 ,与负半轴的交点就表示 .
三、概念剖析
三、概念剖析
事实上,任何一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数,与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
归纳总结
四、典型例题
例1:判断下列语句是否正确:
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
√
√
√
【当堂检测】
1.下列说法正确的是( )
A.实数与数轴上的点是一一对应的
B.无理数的平方一定是无理数
C.有理数都是有限小数
D.实数包括有理数、无理数和零
A
四、典型例题
3,
-3,
0,
π,
3,
归纳总结
四、典型例题
判断对实数进行分类时,应先对某些实数进行计算或化简,然后根据最后的结果分类,例如: =4,它是有理数.由π是无理数,得 是一个无理数,而不是分数,因为分数的分子、分母必须是整数且分母不为0.
【当堂检测】
2.有下列四个论断:
① 是有理数;② 是分数;
③2.131131113…是无理数;④π是无理数,
其中正确的是( )
A.4个 B.3个 C.2个 D.1个
B
【当堂检测】
3.把下列各数分别填入相应的括号内:
,
,
,
,
,
,
,
,
,
,
,
(相邻两个3之间的7的个数逐渐加1)
有理数
无理数
四、典型例题
例3:如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有多少个?
解:∵ ≈1.414,
∴ 和5.1之间的整数有2,3,4,5,
∴A,B两点之间表示整数的点共有4个.
【当堂检测】
4.若将三个数 , , ,表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )
A. B. C. D. 和
B
0
-2
-1
1
3
2
五、课堂总结
实数按定义分类:
正有理数
有理数
实数
无理数
负有理数
0
正无理数
负无理数
实数按大小分类如下:
实数
0
正实数
负实数
正有理数
正无理数
负有理数
负无理数
6.3 实数
第六章 实数
第1课时
一、学习目标
1.能说出无理数和实数的概念,会对实数按一定的标准进行分类.
2.能说明实数和数轴上的点是一一对应的,渗透“数形结合”的思想.
毕德哥拉斯
古希腊著名的数学家毕达哥拉斯曾说过这样的一句话:“世界上只有整数和分数,除此之外就再也没有什么别的数了!”
同学们,你们赞成这位数学家的说法吗
二、新课导入
我们发现,上面的分数都可以写成有限小数或者无限循环小数的形式,即:
我们知道有理数包括整数和分数,请把下列分数写成小数的形式,你有什么发现?
(一)实数的分类
三、概念剖析
事实上,如果把整数看成小数点后是0的小数,那么任何一个有理数可以写成有限小数或无限循环小数的形式.
反过来,任何有限小数或无限循环小数也都是有理数.
新知
三、概念剖析
通过平方根的学习,我们可以知道:
像有理数一样,无理数也有正负之分,例如:
, ,π都是正无理数;
, ,-π都是负无理数;
无限不循环小数:小数位数无限,且小数部分不循环的小数.
无限不循环小数又叫做无理数.
三、概念剖析
有理数和无理数统称为实数.所以实数可以按定义分类如下:
有限小数或
无限循环小数
正有理数
有理数
实数
无理数
负有理数
0
正无理数
负无理数
无限不循环小数
三、概念剖析
由于非0有理数和无理数都有正负之分,实数也有正负之分,所以实数还可以按大小分类如下:
实数
0
正实数
负实数
正有理数
正无理数
负有理数
负无理数
三、概念剖析
(二)实数与数轴
0
1
3
2
4
O'
从上图可以看出,OO'的长是这个圆的周长π,所以点O'对应的数是π.这样,无理数π可以用数轴上的点表示出来.
三、概念剖析
0
-2
-1
1
3
2
如上图,以单位长度为边长画一个正方形,
以原点为圆心,正方形的对角线长为半径画弧,
与正半轴的交点就表示 ,与负半轴的交点就表示 .
三、概念剖析
三、概念剖析
事实上,任何一个无理数都可以用数轴上的一个点表示出来.
当数的范围从有理数扩充到实数后,实数与数轴上的点是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示一个实数,与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大.
归纳总结
四、典型例题
例1:判断下列语句是否正确:
(1)实数不是有理数就是无理数. ( )
(2)无理数都是无限不循环小数. ( )
(4)无理数都是无限小数. ( )
(3)带根号的数都是无理数. ( )
(5)无理数一定都带根号. ( )
×
×
√
√
√
【当堂检测】
1.下列说法正确的是( )
A.实数与数轴上的点是一一对应的
B.无理数的平方一定是无理数
C.有理数都是有限小数
D.实数包括有理数、无理数和零
A
四、典型例题
3,
-3,
0,
π,
3,
归纳总结
四、典型例题
判断对实数进行分类时,应先对某些实数进行计算或化简,然后根据最后的结果分类,例如: =4,它是有理数.由π是无理数,得 是一个无理数,而不是分数,因为分数的分子、分母必须是整数且分母不为0.
【当堂检测】
2.有下列四个论断:
① 是有理数;② 是分数;
③2.131131113…是无理数;④π是无理数,
其中正确的是( )
A.4个 B.3个 C.2个 D.1个
B
【当堂检测】
3.把下列各数分别填入相应的括号内:
,
,
,
,
,
,
,
,
,
,
,
(相邻两个3之间的7的个数逐渐加1)
有理数
无理数
四、典型例题
例3:如图所示,数轴上A,B两点表示的数分别为 和5.1,则A,B两点之间表示整数的点共有多少个?
解:∵ ≈1.414,
∴ 和5.1之间的整数有2,3,4,5,
∴A,B两点之间表示整数的点共有4个.
【当堂检测】
4.若将三个数 , , ,表示在数轴上,其中能被如图所示的墨迹覆盖的数是( )
A. B. C. D. 和
B
0
-2
-1
1
3
2
五、课堂总结
实数按定义分类:
正有理数
有理数
实数
无理数
负有理数
0
正无理数
负无理数
实数按大小分类如下:
实数
0
正实数
负实数
正有理数
正无理数
负有理数
负无理数
