7.1.2 平面直角坐标系 课件 2023-2024学年初中数学人教版七年级下册(19张PPT)
文档属性
| 名称 | 7.1.2 平面直角坐标系 课件 2023-2024学年初中数学人教版七年级下册(19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 470.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 08:04:50 | ||
图片预览


文档简介
(共19张PPT)
第七章 平面直角坐标系
7.1.2 平面直角坐标系
1.知道平面直角坐标系的有关概念,会画平面直角坐标系.
2.知道平面直角坐标系中点的坐标的意义,能由坐标描点和由点写出坐标.
3.知道平面直角坐标系内有几个象限,清楚各象限内点的坐标的符号特点.
4.对于一个图形,能建立合适的坐标系表示图形上各点的坐标.
一、学习目标
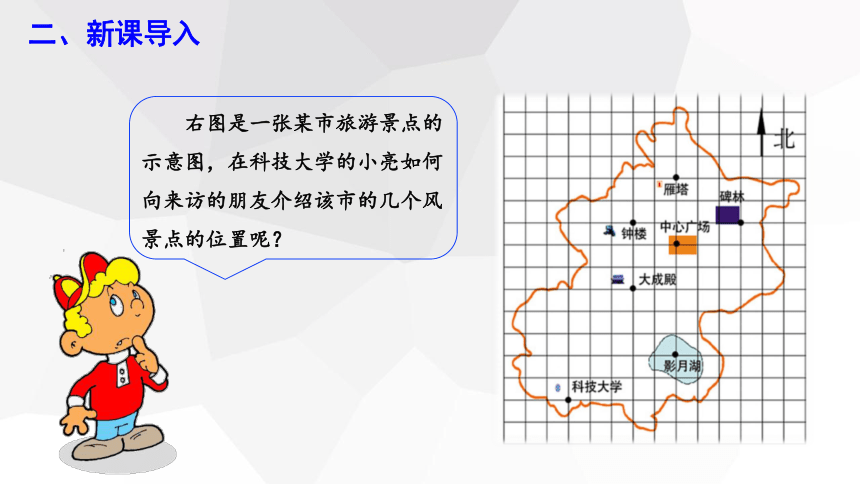
二、新课导入
右图是一张某市旅游景点的示意图,在科技大学的小亮如何向来访的朋友介绍该市的几个风景点的位置呢?
三、概念剖析
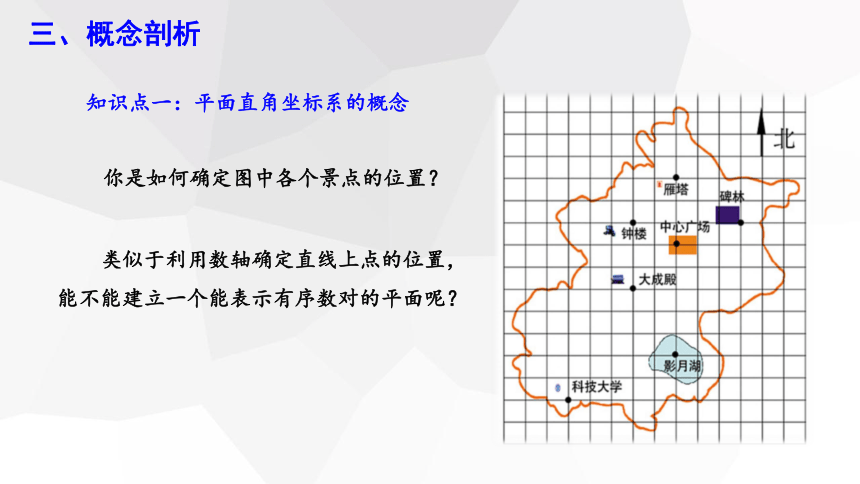
知识点一:平面直角坐标系的概念
你是如何确定图中各个景点的位置?
类似于利用数轴确定直线上点的位置,能不能建立一个能表示有序数对的平面呢?
三、概念剖析
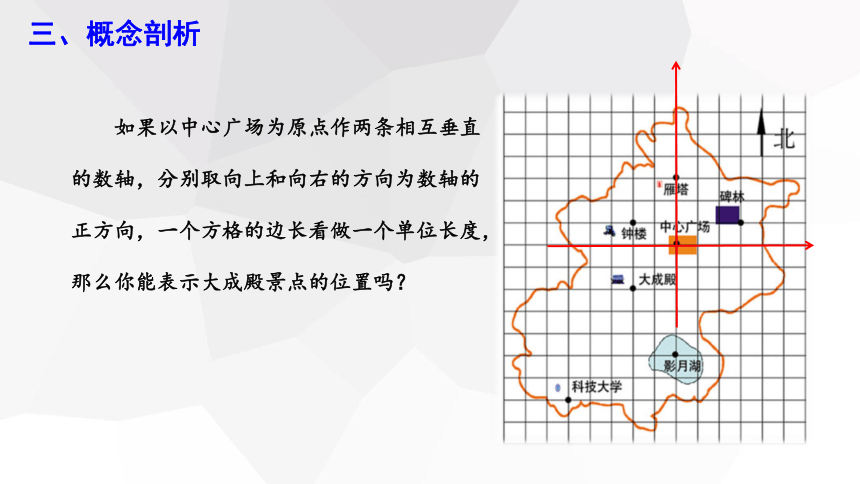
如果以中心广场为原点作两条相互垂直的数轴,分别取向上和向右的方向为数轴的正方向,一个方格的边长看做一个单位长度,那么你能表示大成殿景点的位置吗?
三、概念剖析
x轴或横轴
y轴或纵轴
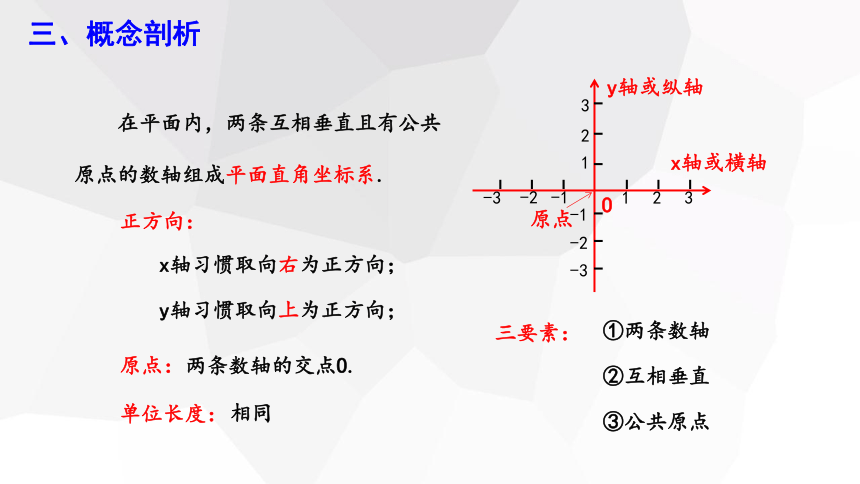
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
正方向:
x轴习惯取向右为正方向;
y轴习惯取向上为正方向;
原点
原点:
两条数轴的交点O.
单位长度:
相同
三要素:
①两条数轴
②互相垂直
③公共原点
1
2
3
-1
-2
-3
-1
-2
-3
1
2
3
O
三、概念剖析
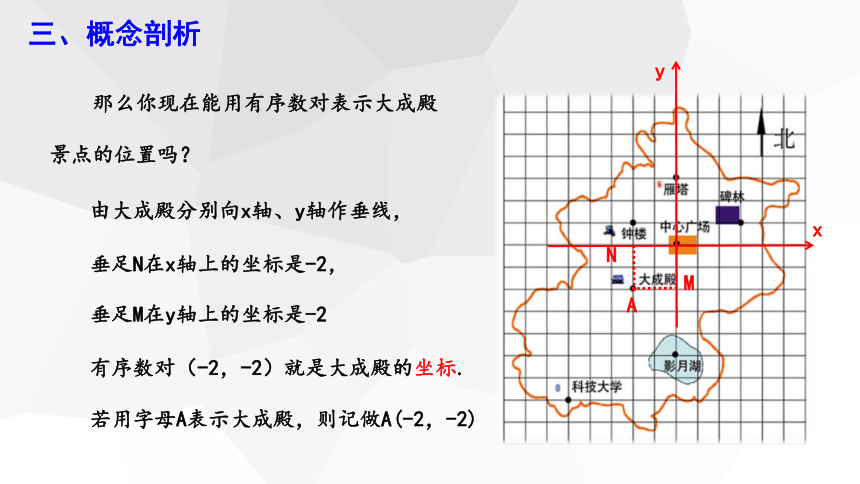
那么你现在能用有序数对表示大成殿景点的位置吗?
x
y
由大成殿分别向x轴、y轴作垂线,
M
N
垂足N在x轴上的坐标是-2,
垂足M在y轴上的坐标是-2
有序数对(-2,-2)就是大成殿的坐标.
若用字母A表示大成殿,则记做A(-2,-2)
A
三、概念剖析
如图,对于平面内任意一点P,过点P向x,y轴作垂线,垂足在x,y轴上的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标.
1
a
3
1
b
3
O
x
y
P(a,b)
归纳总结:
注意:在写点的坐标时,规定横坐标在前,纵坐标在后,中间用逗号隔开.
三、概念剖析
x
y
O
若用字母O表示中心广场,字母B表示雁塔,你能写出他们的坐标吗?
B
点O在x轴和y轴的交点处,故O(0,0);
点B在y轴上,垂足在y轴的坐标为3,故B(0,3);
知识点二:坐标特点及象限划分
原点O的坐标为(0,0);
x轴上的点的纵坐标为0;
y轴上的点的横坐标为0;
归纳总结:
三、概念剖析
建立了平面直角坐标系之后,坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分.每个部分称为象限,两条数轴正半轴所夹部分叫第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限.
第二象限
第一象限
第三象限
第四象限
1
2
3
-1
-2
-3
-1
-2
-3
1
2
3
O
x轴
y轴
如图:
Ⅰ
Ⅱ
Ⅲ
Ⅳ
注意:坐标轴上的点不属于任何象限.
(+,+)
(-,+)
(-,-)
(+,-)
四、典型例题
例1.如下图,以火车站为原点建立平面直角坐标系,一个方格的边长看做一个单位长度,写出市场、文化宫、医院、超市的坐标及所在的象限.
x
y
解:市场的坐标为(4,3),第一象限;
文化宫的坐标为(-3,1),第二象限;
医院的坐标为(-2,-2),第三象限;
超市的坐标为(2,-3),第四象限;
四、典型例题
例2.如图所示的平面直角坐标系中,把以下各组点描出来,并顺次连接各点.
(0,-4),(3,-5),(6,0),(0,-1),(-6,0),(-3,-5),(0,-4).
解:如图所示:
四、典型例题
类似数轴上的点与实数是一一对应的.我们可以得出:
归纳总结:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
【当堂检测】
1.如图,这是某校部分简图,以教学楼为原点建立平面直角坐标系,一个方格的边长看做一个单位长度,分别写出各地的坐标及所在的象限.
办公楼(2,-3),第四象限;
x
y
实验楼(-3,1),第二象限;
解:教学楼(0,0),原点;
礼堂(-2,-2),第三象限;
宿舍(2,2),第一象限;
2.(1)写出图中点A、B、C、D、E、F的坐标及所在象限.
解:A(-3,-2)、第三象限;
【当堂检测】
F(-3,0);x轴
E(2,5),第一象限;
D(0,-3)、y轴;
C(5,-4)、第四象限;
B(-5,4)、第二象限;
【当堂检测】
2.(2)在下图中描出下列各点:L(-5,-3),M(4,0),N(0,5),P(6,2).
解:如图所示:
L
M
N
P
例3.某地为了发展城市群,在现有的四个中小城市A,B,C,D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标.
四、典型例题
E
D
C
B
A
y
解:答案不唯一,
x
可以以点A为坐标原点,建立平面直角坐标系.
此时:A(0,0),
B(11,2),
C(11,9),
D(6,7),
E(2,10)
【当堂检测】
3.右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),求黑棋 、白棋③的坐标.
解:由已知白棋①的坐标是(-2,-1)构建平面直角坐标系,如图:
y
x
y轴应在从左往右数的第四条格线上,且向上为正方向,
x轴在从上往下数第二条格线上,且向右为正方向,
这两条直线的交点为坐标原点,
由此可得黑棋 (1,-2)、
白棋③(-1,-3)
o
五、课堂总结
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
(一)平面直角坐标系的概念
如图所示,有序数对(a,b)叫做点P的坐标.
1
a
3
1
b
3
O
x
y
P(a,b)
(二)坐标特点及象限划分
原点O的坐标为(0,0);
x轴上的点的纵坐标为0;
y轴上的点的横坐标为0;
第二象限
第一象限
第三象限
第四象限
1
2
3
-1
-2
-3
-1
-2
-3
1
2
3
x
y
第七章 平面直角坐标系
7.1.2 平面直角坐标系
1.知道平面直角坐标系的有关概念,会画平面直角坐标系.
2.知道平面直角坐标系中点的坐标的意义,能由坐标描点和由点写出坐标.
3.知道平面直角坐标系内有几个象限,清楚各象限内点的坐标的符号特点.
4.对于一个图形,能建立合适的坐标系表示图形上各点的坐标.
一、学习目标
二、新课导入
右图是一张某市旅游景点的示意图,在科技大学的小亮如何向来访的朋友介绍该市的几个风景点的位置呢?
三、概念剖析
知识点一:平面直角坐标系的概念
你是如何确定图中各个景点的位置?
类似于利用数轴确定直线上点的位置,能不能建立一个能表示有序数对的平面呢?
三、概念剖析
如果以中心广场为原点作两条相互垂直的数轴,分别取向上和向右的方向为数轴的正方向,一个方格的边长看做一个单位长度,那么你能表示大成殿景点的位置吗?
三、概念剖析
x轴或横轴
y轴或纵轴
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
正方向:
x轴习惯取向右为正方向;
y轴习惯取向上为正方向;
原点
原点:
两条数轴的交点O.
单位长度:
相同
三要素:
①两条数轴
②互相垂直
③公共原点
1
2
3
-1
-2
-3
-1
-2
-3
1
2
3
O
三、概念剖析
那么你现在能用有序数对表示大成殿景点的位置吗?
x
y
由大成殿分别向x轴、y轴作垂线,
M
N
垂足N在x轴上的坐标是-2,
垂足M在y轴上的坐标是-2
有序数对(-2,-2)就是大成殿的坐标.
若用字母A表示大成殿,则记做A(-2,-2)
A
三、概念剖析
如图,对于平面内任意一点P,过点P向x,y轴作垂线,垂足在x,y轴上的数a,b分别叫做点P的横坐标、纵坐标,有序数对(a,b)叫做点P的坐标.
1
a
3
1
b
3
O
x
y
P(a,b)
归纳总结:
注意:在写点的坐标时,规定横坐标在前,纵坐标在后,中间用逗号隔开.
三、概念剖析
x
y
O
若用字母O表示中心广场,字母B表示雁塔,你能写出他们的坐标吗?
B
点O在x轴和y轴的交点处,故O(0,0);
点B在y轴上,垂足在y轴的坐标为3,故B(0,3);
知识点二:坐标特点及象限划分
原点O的坐标为(0,0);
x轴上的点的纵坐标为0;
y轴上的点的横坐标为0;
归纳总结:
三、概念剖析
建立了平面直角坐标系之后,坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分.每个部分称为象限,两条数轴正半轴所夹部分叫第一象限,其他三个部分按逆时针方向依次叫做第二象限、第三象限和第四象限.
第二象限
第一象限
第三象限
第四象限
1
2
3
-1
-2
-3
-1
-2
-3
1
2
3
O
x轴
y轴
如图:
Ⅰ
Ⅱ
Ⅲ
Ⅳ
注意:坐标轴上的点不属于任何象限.
(+,+)
(-,+)
(-,-)
(+,-)
四、典型例题
例1.如下图,以火车站为原点建立平面直角坐标系,一个方格的边长看做一个单位长度,写出市场、文化宫、医院、超市的坐标及所在的象限.
x
y
解:市场的坐标为(4,3),第一象限;
文化宫的坐标为(-3,1),第二象限;
医院的坐标为(-2,-2),第三象限;
超市的坐标为(2,-3),第四象限;
四、典型例题
例2.如图所示的平面直角坐标系中,把以下各组点描出来,并顺次连接各点.
(0,-4),(3,-5),(6,0),(0,-1),(-6,0),(-3,-5),(0,-4).
解:如图所示:
四、典型例题
类似数轴上的点与实数是一一对应的.我们可以得出:
归纳总结:
①对于坐标平面内任意一点M,都有唯一的一对有序实数(x,y) (即点M的坐标)和它对应;
②反过来,对于任意一对有序实数(x,y),在坐标平面内都有唯一的一点M(即坐标为(x,y)的点)和它对应.
也就是说,坐标平面内的点与有序实数对是一一对应的.
【当堂检测】
1.如图,这是某校部分简图,以教学楼为原点建立平面直角坐标系,一个方格的边长看做一个单位长度,分别写出各地的坐标及所在的象限.
办公楼(2,-3),第四象限;
x
y
实验楼(-3,1),第二象限;
解:教学楼(0,0),原点;
礼堂(-2,-2),第三象限;
宿舍(2,2),第一象限;
2.(1)写出图中点A、B、C、D、E、F的坐标及所在象限.
解:A(-3,-2)、第三象限;
【当堂检测】
F(-3,0);x轴
E(2,5),第一象限;
D(0,-3)、y轴;
C(5,-4)、第四象限;
B(-5,4)、第二象限;
【当堂检测】
2.(2)在下图中描出下列各点:L(-5,-3),M(4,0),N(0,5),P(6,2).
解:如图所示:
L
M
N
P
例3.某地为了发展城市群,在现有的四个中小城市A,B,C,D附近新建机场E,试建立适当的直角坐标系,并写出各点的坐标.
四、典型例题
E
D
C
B
A
y
解:答案不唯一,
x
可以以点A为坐标原点,建立平面直角坐标系.
此时:A(0,0),
B(11,2),
C(11,9),
D(6,7),
E(2,10)
【当堂检测】
3.右图是一个围棋棋盘(局部),把这个围棋棋盘放置在一个平面直角坐标系中,白棋①的坐标是(-2,-1),求黑棋 、白棋③的坐标.
解:由已知白棋①的坐标是(-2,-1)构建平面直角坐标系,如图:
y
x
y轴应在从左往右数的第四条格线上,且向上为正方向,
x轴在从上往下数第二条格线上,且向右为正方向,
这两条直线的交点为坐标原点,
由此可得黑棋 (1,-2)、
白棋③(-1,-3)
o
五、课堂总结
在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.
(一)平面直角坐标系的概念
如图所示,有序数对(a,b)叫做点P的坐标.
1
a
3
1
b
3
O
x
y
P(a,b)
(二)坐标特点及象限划分
原点O的坐标为(0,0);
x轴上的点的纵坐标为0;
y轴上的点的横坐标为0;
第二象限
第一象限
第三象限
第四象限
1
2
3
-1
-2
-3
-1
-2
-3
1
2
3
x
y
