8.3 实际问题与二元一次方程组(第3课时) 课件 14张PPT 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 8.3 实际问题与二元一次方程组(第3课时) 课件 14张PPT 2023-2024学年初中数学人教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 247.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 08:40:53 | ||
图片预览




文档简介
(共14张PPT)
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
第3课时
一、学习目标
1.会用列表法分析应用题中的数量关系,列出相应的二元一次方程组解决较复杂的实际问题,并进一步增强解方程组的技能.
2.学会从图表中获取信息的方法,进一步感受间接设未知数解决问题的解题策略.
二、新课导入
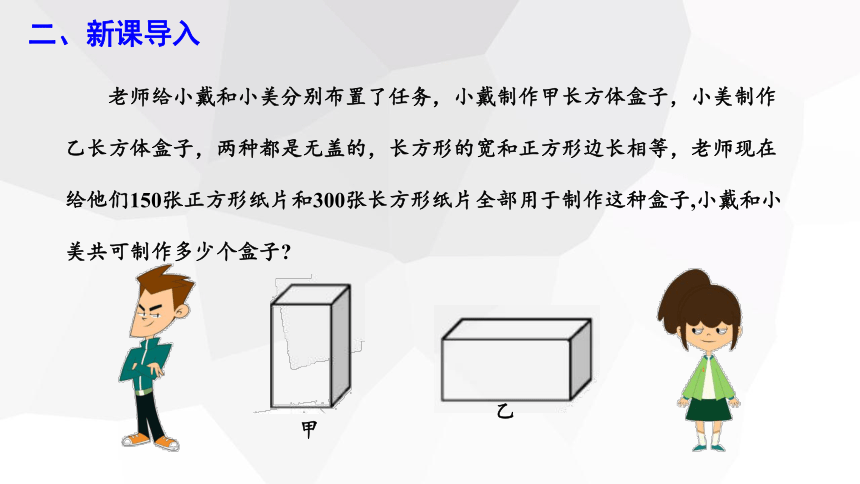
老师给小戴和小美分别布置了任务,小戴制作甲长方体盒子,小美制作乙长方体盒子,两种都是无盖的,长方形的宽和正方形边长相等,老师现在给他们150张正方形纸片和300张长方形纸片全部用于制作这种盒子,小戴和小美共可制作多少个盒子
乙
甲
三、典型例题
(一)用二元一次方程组解列表问题
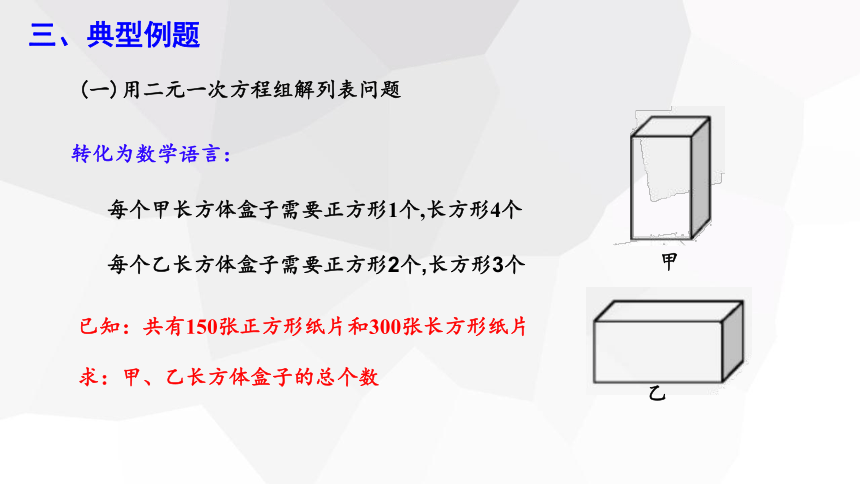
转化为数学语言:
已知:共有150张正方形纸片和300张长方形纸片
每个甲长方体盒子需要正方形1个,长方形4个
每个乙长方体盒子需要正方形2个,长方形3个
乙
甲
求:甲、乙长方体盒子的总个数
三、典型例题
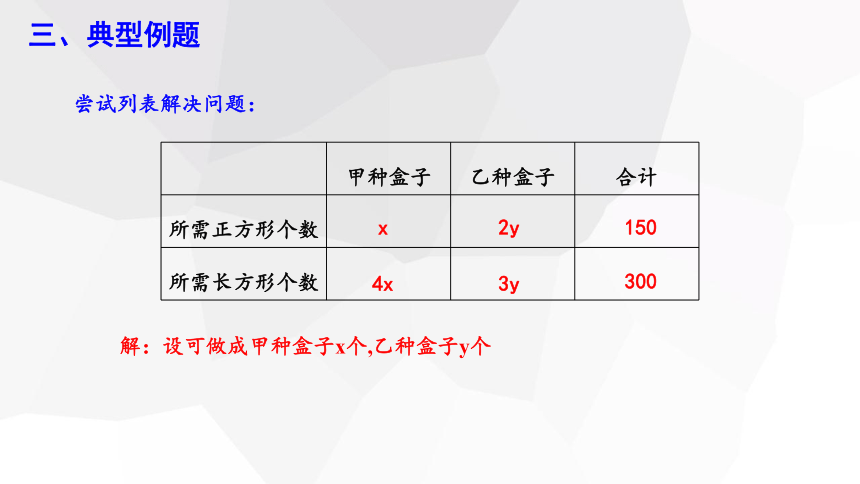
尝试列表解决问题:
解:设可做成甲种盒子x个,乙种盒子y个
甲种盒子 乙种盒子 合计
所需正方形个数
所需长方形个数
x
4x
2y
3y
150
300
整理可得到:
解这个方程组,得
甲长方体盒子+乙长方体盒子=30+60=90
三、典型例题
答:共可制作90个盒子.
三、典型例题
解决比较复杂的应用题时,可以先从问题入手,看要解决的问题是什么,再画表格或图形,分析题中的数量关系,从而找到等量关系,列出方程(组).
归纳总结:
【当堂检测】
1.小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表:
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购物 6 5 1140
第二次购物 3 7 1110
第三次购物 9 8 1062
求商品A、B的标价.
【当堂检测】
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购物 6 5 1140
第二次购物 3 7 1110
第三次购物 9 8 1062
解:设商品A的标价为x元,商品B的标价为y元,
解这个方程组,得
答:商品A的标价为90元,商品B的标价为120元;
可得:
三、典型例题
例2.一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两装修组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天也可以完成,需付两装修组费用共3480元.
(1)求甲、乙两组单独完成各需多少天
(二)用二元一次方程组解工程问题
若设甲装修组一天的工作量为a,乙装修组一天的工作量为b,
解:根据题意,甲、乙两个装修组一天的工作量是 ,
可得:
解得
所以甲组单独完成需 天,乙组单独完成需 天
三、典型例题
(2)如果选择一个装修组单独完成此项装修任务,从节约开支的角度考虑,那么这家商店应选择哪个装修组
解:设甲装修组每天的费用为m元,乙装修组每天的费用为n元,
可得:
解得
所以甲组单独完成需300×12=3600(元),
故从节约开支的角度考虑,应选择乙组单独完成.
乙组单独完成需140×24=3360(元).
实际问题
数学问题的解
(二元一次方程组的解)
问题答案
数学问题
(二元一次方程组)
设未知数,列方程组
转化
解方程组
检验
三、典型例题
【当堂检测】
2.某公司拟派A、B两个工程队共同建设某区域的绿化带.已知A工程队2人与B工程队3人每天共完成310米绿化带,A工程队的5人与B工程队的6人每天共完成700米绿化带,求A队每人每天和B队每人每天各完成多少米绿化带.
依题意可列方程组
解得
答:A队每人每天完成80米,B队每人每天完成50米绿化带.
解:设A队每人每天完成x米,B队每人每天完成y米绿化带
四、课堂总结
解决比较复杂的应用题时,可以先从问题入手,看要解决的问题是什么,再画表格或图形,分析题中的数量关系,从而找到等量关系,列出方程(组).
第八章 二元一次方程组
8.3 实际问题与二元一次方程组
第3课时
一、学习目标
1.会用列表法分析应用题中的数量关系,列出相应的二元一次方程组解决较复杂的实际问题,并进一步增强解方程组的技能.
2.学会从图表中获取信息的方法,进一步感受间接设未知数解决问题的解题策略.
二、新课导入
老师给小戴和小美分别布置了任务,小戴制作甲长方体盒子,小美制作乙长方体盒子,两种都是无盖的,长方形的宽和正方形边长相等,老师现在给他们150张正方形纸片和300张长方形纸片全部用于制作这种盒子,小戴和小美共可制作多少个盒子
乙
甲
三、典型例题
(一)用二元一次方程组解列表问题
转化为数学语言:
已知:共有150张正方形纸片和300张长方形纸片
每个甲长方体盒子需要正方形1个,长方形4个
每个乙长方体盒子需要正方形2个,长方形3个
乙
甲
求:甲、乙长方体盒子的总个数
三、典型例题
尝试列表解决问题:
解:设可做成甲种盒子x个,乙种盒子y个
甲种盒子 乙种盒子 合计
所需正方形个数
所需长方形个数
x
4x
2y
3y
150
300
整理可得到:
解这个方程组,得
甲长方体盒子+乙长方体盒子=30+60=90
三、典型例题
答:共可制作90个盒子.
三、典型例题
解决比较复杂的应用题时,可以先从问题入手,看要解决的问题是什么,再画表格或图形,分析题中的数量关系,从而找到等量关系,列出方程(组).
归纳总结:
【当堂检测】
1.小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折,其余两次均按标价购买,三次购买商品A、B的数量和费用如下表:
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购物 6 5 1140
第二次购物 3 7 1110
第三次购物 9 8 1062
求商品A、B的标价.
【当堂检测】
购买商品A的数量(个) 购买商品B的数量(个) 购买总费用(元)
第一次购物 6 5 1140
第二次购物 3 7 1110
第三次购物 9 8 1062
解:设商品A的标价为x元,商品B的标价为y元,
解这个方程组,得
答:商品A的标价为90元,商品B的标价为120元;
可得:
三、典型例题
例2.一家商店进行装修,若请甲、乙两个装修组同时施工,8天可以完成,需付两装修组费用共3520元;若先请甲组单独做6天,再请乙组单独做12天也可以完成,需付两装修组费用共3480元.
(1)求甲、乙两组单独完成各需多少天
(二)用二元一次方程组解工程问题
若设甲装修组一天的工作量为a,乙装修组一天的工作量为b,
解:根据题意,甲、乙两个装修组一天的工作量是 ,
可得:
解得
所以甲组单独完成需 天,乙组单独完成需 天
三、典型例题
(2)如果选择一个装修组单独完成此项装修任务,从节约开支的角度考虑,那么这家商店应选择哪个装修组
解:设甲装修组每天的费用为m元,乙装修组每天的费用为n元,
可得:
解得
所以甲组单独完成需300×12=3600(元),
故从节约开支的角度考虑,应选择乙组单独完成.
乙组单独完成需140×24=3360(元).
实际问题
数学问题的解
(二元一次方程组的解)
问题答案
数学问题
(二元一次方程组)
设未知数,列方程组
转化
解方程组
检验
三、典型例题
【当堂检测】
2.某公司拟派A、B两个工程队共同建设某区域的绿化带.已知A工程队2人与B工程队3人每天共完成310米绿化带,A工程队的5人与B工程队的6人每天共完成700米绿化带,求A队每人每天和B队每人每天各完成多少米绿化带.
依题意可列方程组
解得
答:A队每人每天完成80米,B队每人每天完成50米绿化带.
解:设A队每人每天完成x米,B队每人每天完成y米绿化带
四、课堂总结
解决比较复杂的应用题时,可以先从问题入手,看要解决的问题是什么,再画表格或图形,分析题中的数量关系,从而找到等量关系,列出方程(组).
