9.1.2 不等式的性质 第1课时 课件(共16张PPT) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 9.1.2 不等式的性质 第1课时 课件(共16张PPT) 2023-2024学年初中数学人教版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 16.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 08:46:27 | ||
图片预览





文档简介
(共16张PPT)
第九章 不等式与不等式组
9.1.2 不等式的性质
第1课时
1.通过计算、观察、分析、验证归纳出不等式的三个性质.
2.经历不等式性质的探索过程,初步体会不等式与等式的异同.
一、学习目标
二、新课导入
以前我们学习了哪些等式的性质?
思考:那同学们猜一猜不等式有哪些性质.
复习导入:
等式的性质1:如果 a = b,那么 a + c = b + c,a – c = b – c;
等式的性质2:如果 a = b,那么 ac = bc , (c ≠ 0).
三、概念剖析
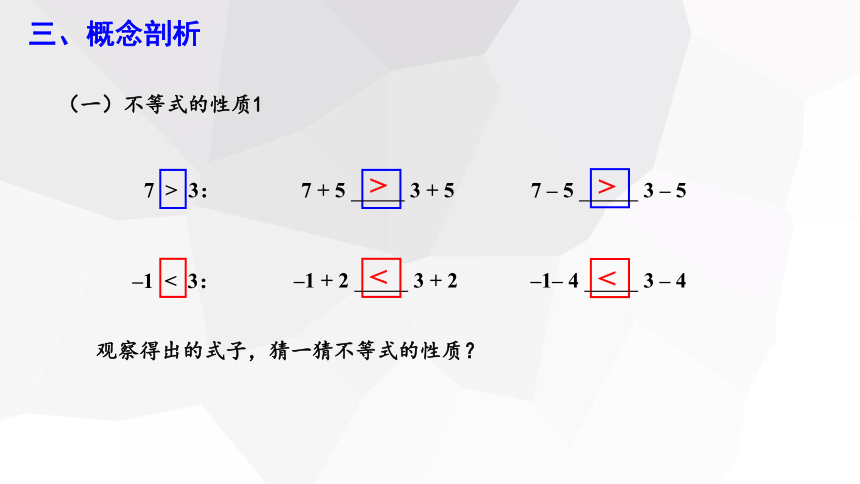
(一)不等式的性质1
>
<
<
–1 < 3:
–1 + 2 3 + 2
–1– 4 3 – 4
>
7 > 3:
7 + 5 3 + 5
7 – 5 3 – 5
观察得出的式子,猜一猜不等式的性质?
三、概念剖析
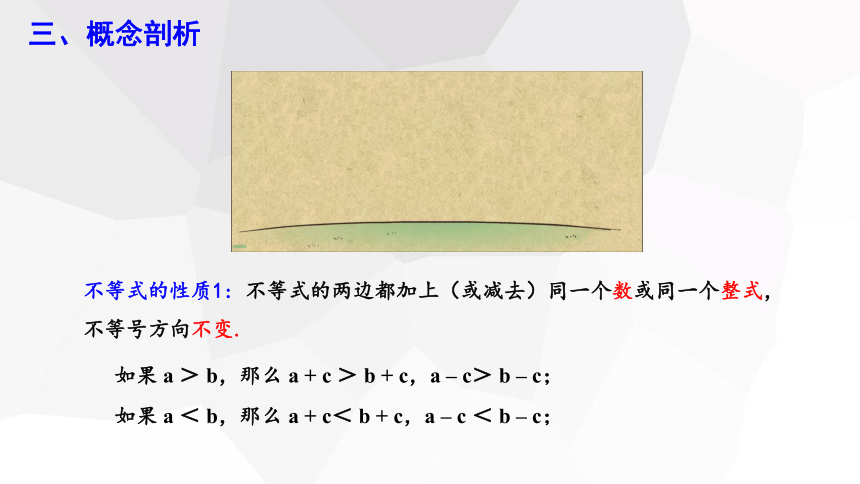
不等式的性质1: 不等式的两边都加上(或减去)同一个数或同一个整式,不等号方向不变.
如果 a > b,那么 a + c > b + c,a – c> b – c;
如果 a < b,那么 a + c< b + c,a – c < b – c;
例 1:已知 a > b,用“ > ”或“ < ”完成下列填空.
典型例题
注:这里的不等式变形类似与方程的变形中的“移项”.
>
(1)a + 2 b + 2;
(2)a – 2 b – 2;
(3)a + c b + c;
(4)a – c b – c;
>
>
>
【当堂检测】
1.下列不等式中不成立的是( )
A.若a<2,则a+2<4 B.若b<0,则b-2<-2
C.若a<b,则a-1>b-1
D.若a>b,则a-x>b-x
C
三、概念剖析
已知 7 > 3
那么 7×5 ____ 3× 5 ,
>
那么-1×2____3×2,
<
观察得出的式子,猜一猜不等式的性质?
7÷5 ____ 3÷ 5 ,
>
-1÷2____3÷2,
<
(二)不等式的性质2
已知 -1< 3
三、概念剖析
不等式基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即如果a>b,c>0,那么 ac>bc,
例 2:已知 a > b,且 c > 0,用“ > ”或“ < ”完成下列填空.
(二)用性质2解简单不等式
典型例题
>
(1)a × 3 b × 3;
(2)a ÷ 2 b ÷ 2;
(3)a × c b × c;
(4)a ÷ c b ÷ c;
>
>
>
【当堂检测】
(2) x<-3;
(2)根据不等式的基本性质2,
即x<-21.
2.把下列不等式化成“x> a”或“x<a”的形式.
即x>-2
(1) x> -1.
解:(1)根据不等式的基本性质2,
两边都乘以2,不等号的方向不变
两边都乘7,不等号的方向不变,
三、概念剖析
7 ÷ (-5)____3÷ (-5)
<
-1÷ (- 4)____3÷ ( - 4)
>
已知 7 > 3
已知 -1< 3
观察得出的式子,猜一猜不等式的性质?
7 ×(-5)____3×(-5),
<
-1×(- 4)____3×( - 4),
>
(三)不等式的性质3
三、概念剖析
不等式基本性质3:
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即如果a > b,c < 0,那么 ac < bc,
例3:已知 a > b,且 c < 0,用“ > ”或“ < ”完成下列填空.
典型例题
<
(1)a × (–1) b × (–1) ;
(2)a ÷ (–1) b ÷ (–1) ;
(3)a × c b × c;
(4)a ÷ c b ÷ c;
<
<
<
注意:应用不等式的基本性质3时,要改变不等号的方向
【当堂检测】
3.小辉在学了不等式的基本性质这一节后,他觉得很容易,并用很快的速度做了两道填空题,结果如下:
(1)若x<0,则3x < 5x;
(2)若x>y,则xz2 > yz2.
你同意他的做法吗
解:不同意.
(1)中,3<5,乘以负数x,根据不等式的性质3,应是>;
(2)中,z可能是0,若z是0时,xz2=yz2.
四、课堂总结
不等式基本性质1:
不等式的两边都加上(或减去)同一数或同一个整式,不等号的方向不变.
不等式基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向 不变.
不等式基本性质3:
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
第九章 不等式与不等式组
9.1.2 不等式的性质
第1课时
1.通过计算、观察、分析、验证归纳出不等式的三个性质.
2.经历不等式性质的探索过程,初步体会不等式与等式的异同.
一、学习目标
二、新课导入
以前我们学习了哪些等式的性质?
思考:那同学们猜一猜不等式有哪些性质.
复习导入:
等式的性质1:如果 a = b,那么 a + c = b + c,a – c = b – c;
等式的性质2:如果 a = b,那么 ac = bc , (c ≠ 0).
三、概念剖析
(一)不等式的性质1
>
<
<
–1 < 3:
–1 + 2 3 + 2
–1– 4 3 – 4
>
7 > 3:
7 + 5 3 + 5
7 – 5 3 – 5
观察得出的式子,猜一猜不等式的性质?
三、概念剖析
不等式的性质1: 不等式的两边都加上(或减去)同一个数或同一个整式,不等号方向不变.
如果 a > b,那么 a + c > b + c,a – c> b – c;
如果 a < b,那么 a + c< b + c,a – c < b – c;
例 1:已知 a > b,用“ > ”或“ < ”完成下列填空.
典型例题
注:这里的不等式变形类似与方程的变形中的“移项”.
>
(1)a + 2 b + 2;
(2)a – 2 b – 2;
(3)a + c b + c;
(4)a – c b – c;
>
>
>
【当堂检测】
1.下列不等式中不成立的是( )
A.若a<2,则a+2<4 B.若b<0,则b-2<-2
C.若a<b,则a-1>b-1
D.若a>b,则a-x>b-x
C
三、概念剖析
已知 7 > 3
那么 7×5 ____ 3× 5 ,
>
那么-1×2____3×2,
<
观察得出的式子,猜一猜不等式的性质?
7÷5 ____ 3÷ 5 ,
>
-1÷2____3÷2,
<
(二)不等式的性质2
已知 -1< 3
三、概念剖析
不等式基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向不变.
即如果a>b,c>0,那么 ac>bc,
例 2:已知 a > b,且 c > 0,用“ > ”或“ < ”完成下列填空.
(二)用性质2解简单不等式
典型例题
>
(1)a × 3 b × 3;
(2)a ÷ 2 b ÷ 2;
(3)a × c b × c;
(4)a ÷ c b ÷ c;
>
>
>
【当堂检测】
(2) x<-3;
(2)根据不等式的基本性质2,
即x<-21.
2.把下列不等式化成“x> a”或“x<a”的形式.
即x>-2
(1) x> -1.
解:(1)根据不等式的基本性质2,
两边都乘以2,不等号的方向不变
两边都乘7,不等号的方向不变,
三、概念剖析
7 ÷ (-5)____3÷ (-5)
<
-1÷ (- 4)____3÷ ( - 4)
>
已知 7 > 3
已知 -1< 3
观察得出的式子,猜一猜不等式的性质?
7 ×(-5)____3×(-5),
<
-1×(- 4)____3×( - 4),
>
(三)不等式的性质3
三、概念剖析
不等式基本性质3:
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
即如果a > b,c < 0,那么 ac < bc,
例3:已知 a > b,且 c < 0,用“ > ”或“ < ”完成下列填空.
典型例题
<
(1)a × (–1) b × (–1) ;
(2)a ÷ (–1) b ÷ (–1) ;
(3)a × c b × c;
(4)a ÷ c b ÷ c;
<
<
<
注意:应用不等式的基本性质3时,要改变不等号的方向
【当堂检测】
3.小辉在学了不等式的基本性质这一节后,他觉得很容易,并用很快的速度做了两道填空题,结果如下:
(1)若x<0,则3x < 5x;
(2)若x>y,则xz2 > yz2.
你同意他的做法吗
解:不同意.
(1)中,3<5,乘以负数x,根据不等式的性质3,应是>;
(2)中,z可能是0,若z是0时,xz2=yz2.
四、课堂总结
不等式基本性质1:
不等式的两边都加上(或减去)同一数或同一个整式,不等号的方向不变.
不等式基本性质2:
不等式的两边都乘(或除以)同一个正数,不等号的方向 不变.
不等式基本性质3:
不等式的两边都乘(或除以)同一个负数,不等号的方向改变.
