第八章二元一次方程组 复习课 课件(共19张PPT) 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第八章二元一次方程组 复习课 课件(共19张PPT) 2023-2024学年初中数学人教版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 175.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 08:50:45 | ||
图片预览





文档简介
(共19张PPT)
第八章 二元一次方程组
复习课
一、学习目标
1.知道二元一次方程的相关概念,会解二元一次方程.
2.知道二元一次方程组和三元一次方程组的相关概念,能运用代入消元法和加减消元法解二元一次方程组和三元一次方程组.
3.能找出实际问题中的等量关系,运用方程模型解决实际问题.
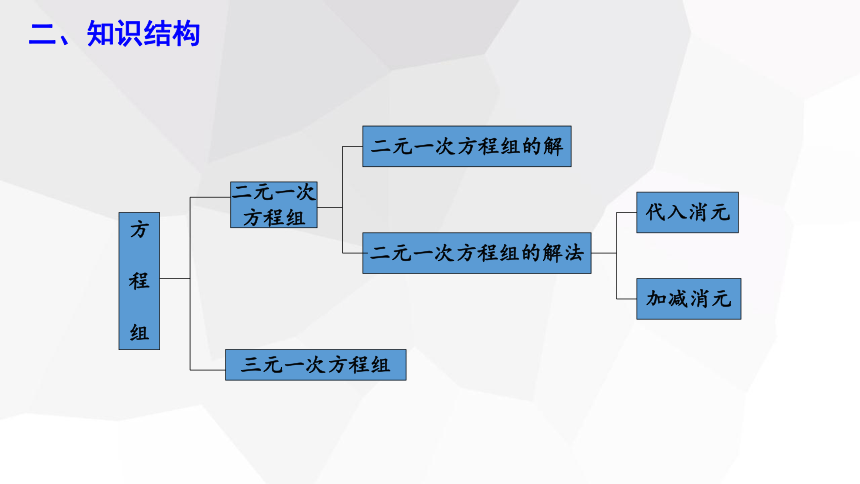
二、知识结构
方
程
组
二元一次
方程组
三元一次方程组
二元一次方程组的解
二元一次方程组的解法
代入消元
加减消元
一、二元一次方程(组)的相关概念
三、知识回顾
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
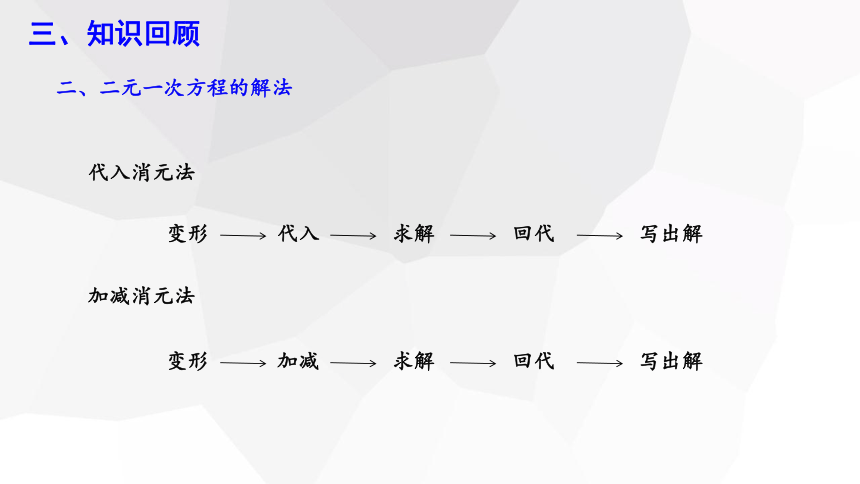
二、二元一次方程的解法
三、知识回顾
代入消元法
变形
代入
求解
回代
写出解
加减消元法
变形
加减
求解
回代
写出解
三、列二元一次方程组解决实际问题
三、知识回顾
(1)审题:审清题目,明确题目中的数量关系,属于哪一类应用题
(5)检验作答:检验所列方程的解是否符合题意,写出答案,并带上单位
(4)解方程:正确解方程,并求出所要求的量
(3)列方程:找出等量关系,并准确用代数式表示题中的数量,列出方程组
(2)设元:引入未知数,并标注单位,一般有直接设元、间接设元和设辅助未知数
三、知识回顾
含有三个未知数,方程中所含未知数的项的次数都是1,这样的方程叫做三元一次方程.
共含有三个未知数的三个一次方程所组成的一组方程,叫做三元一次方程组.
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
解三元一次方程组的基本思路:
四、三元一次方程(组)
四、典型例题
例1.若x3a-2b-2-2ya+b=5是二元一次方程,则a=_______,b=_______.
解析:因为x3a-2b-2-2ya+b=5是二元一次方程,
分析:根据二元一次方程的定义得出关于a、b的方程组,求出方程组的解.
所以
解得:a=1,b=0
0
1
(一)、二元一次方程的概念
1.已知方程xm-2+y2m-n=3是二元一次方程,则m+n=_______.
解析:由题意可知:m-2=1,2m-n=1,
所以m=3,n=5,
m+n=8,
故答案为:8
8
【当堂检测】
(二)、二(三)元一次方程组的解法
四、典型例题
①②
解:①﹣②,得: 4y=﹣28,
①②
解:①变形为:x=4+2y ③
例2.解下列方程组
(1) (2)
所以原方程组的解为
解得:x=﹣5,
将y=﹣7代入①,得:3x+7=﹣8,
解得:y=﹣7,
所以原方程组的解为
解得:x=8
把y=2代入④,得:x=2×2+4
解得:y=2
把③代入②,得:
四、典型例题
解:① + ② 得:3x – 3y = 15,即 x – y = 5 ④;
② – ③ 得:x + 2y = 11 ⑤;
⑤–④:得 3y = 6,即 y = 2;
所以原方程组的解为:
将 y = 2 代入 ④ 得:x = 7;
把 x = 7,y = 2 代入 ③ 得:z = – 2;
(3)
①②
③
解:① + ② 得:x + y = 2 ④;
2. 解方程组:
①②
③
① + ③ 得:7x – 2y = 32 ⑤;
所以原方程组的解为:
把 x = 4,y = – 2 代入 ② 得:z = 0;
联立 ④ ⑤ 得:
④
⑤
解得:
【当堂检测】
3.关于x、y的方程组 的解是 ,求 m2 – n2 的值.
所以 m2 – n2 = 4 – 9 = – 5.
【当堂检测】
解:已知:关于x、y的方程组 的解是 ;
把 x = 1,y = 1 代入上述方程组可得:
解得:m = 2,n = 3;
四、典型例题
(三)、利用一次方程组解决实际问题
例3.某校订购了A、B两种笔记本,A种笔记本单价为28元,B种单价为24元,若B种笔记本的订购数量比A种笔记本的2倍少20个,并且订购两种笔记本共用了2560元.问该校分别订购了A、B两种笔记本各多少个?
分析:根据“B种笔记本的订购数量比A种笔记本的2倍少20个”和“两种笔记本共用了2560元”列方程组求解.
等量关系: B种笔记本的订购数量 = A种笔记本的数量×2 – 20;
B种笔记本费用 + A种笔记本费用 = 2560;
四、典型例题
解:设该校订购了A种笔记本 x 个,B种笔记本 y 个;
方程组的解:
答:该校订购了A种笔记本40个,B种笔记本60个.
根据题意,得:
①
②
把 ① 代入 ② 得:76x = 3040;
解得:x = 40;
把 x = 40 代入 ① 得:y = 60;
【当堂检测】
4. 某酒店客房有三人间、双人间客房,收费数据如表所示:
普通(元/间/天) 豪华(元/间/天)
三人间 150 300
双人间 140 400
为吸引游客,实行团体入住五折优惠措施,一个 50 人的旅游团优惠期间到该酒店入住,住了一些三人普通间和双人普通间客房,若每间客房正好住满,且一天共花去住宿费 1510 元,则旅游团住了三人普通间和双人普通间客房多少间?
【当堂检测】
普通(元/间/天) 豪华(元/间/天)
三人间 150 300
双人间 140 400
解:设三人普通间共住了 x 人,则双人普通间共住了 y 人;
解得:
三人间: (间) 双人间: (间)
根据题意得:
答:旅游团住了三人普通间客房 8 间,双人普通间客房 13 间.
5.甲、乙、丙三种商品,若买甲4件,乙5件,丙2件,共用69元;若买甲5件,乙6件,丙1件,共用84元.问买甲2件,乙3件,丙4件,共需要多少元?
解:设三种商品甲、乙、丙的单价分别是a、b、c元;
①
②
可得方程组
① × 3 – ② × 2 得:
2a + 3b + 4c = 39(元)
答:买甲2件,乙3件,丙4件,共需要39元.
【当堂检测】
五、课堂总结
代入法
加减法
实际应用
三元一次方程组
二元一次方程组
二元一次方程
解法
包含
应用
拓展
第八章 二元一次方程组
复习课
一、学习目标
1.知道二元一次方程的相关概念,会解二元一次方程.
2.知道二元一次方程组和三元一次方程组的相关概念,能运用代入消元法和加减消元法解二元一次方程组和三元一次方程组.
3.能找出实际问题中的等量关系,运用方程模型解决实际问题.
二、知识结构
方
程
组
二元一次
方程组
三元一次方程组
二元一次方程组的解
二元一次方程组的解法
代入消元
加减消元
一、二元一次方程(组)的相关概念
三、知识回顾
含有两个未知数,并且所含未知数的项的次数都是1的方程叫做二元一次方程.
共含有两个未知数的两个一次方程所组成的一组方程,叫做二元一次方程组.
二元一次方程组中各个方程的公共解,叫做这个二元一次方程组的解.
二、二元一次方程的解法
三、知识回顾
代入消元法
变形
代入
求解
回代
写出解
加减消元法
变形
加减
求解
回代
写出解
三、列二元一次方程组解决实际问题
三、知识回顾
(1)审题:审清题目,明确题目中的数量关系,属于哪一类应用题
(5)检验作答:检验所列方程的解是否符合题意,写出答案,并带上单位
(4)解方程:正确解方程,并求出所要求的量
(3)列方程:找出等量关系,并准确用代数式表示题中的数量,列出方程组
(2)设元:引入未知数,并标注单位,一般有直接设元、间接设元和设辅助未知数
三、知识回顾
含有三个未知数,方程中所含未知数的项的次数都是1,这样的方程叫做三元一次方程.
共含有三个未知数的三个一次方程所组成的一组方程,叫做三元一次方程组.
三元一次方程组
二元一次方程组
一元一次方程
消元
消元
解三元一次方程组的基本思路:
四、三元一次方程(组)
四、典型例题
例1.若x3a-2b-2-2ya+b=5是二元一次方程,则a=_______,b=_______.
解析:因为x3a-2b-2-2ya+b=5是二元一次方程,
分析:根据二元一次方程的定义得出关于a、b的方程组,求出方程组的解.
所以
解得:a=1,b=0
0
1
(一)、二元一次方程的概念
1.已知方程xm-2+y2m-n=3是二元一次方程,则m+n=_______.
解析:由题意可知:m-2=1,2m-n=1,
所以m=3,n=5,
m+n=8,
故答案为:8
8
【当堂检测】
(二)、二(三)元一次方程组的解法
四、典型例题
①②
解:①﹣②,得: 4y=﹣28,
①②
解:①变形为:x=4+2y ③
例2.解下列方程组
(1) (2)
所以原方程组的解为
解得:x=﹣5,
将y=﹣7代入①,得:3x+7=﹣8,
解得:y=﹣7,
所以原方程组的解为
解得:x=8
把y=2代入④,得:x=2×2+4
解得:y=2
把③代入②,得:
四、典型例题
解:① + ② 得:3x – 3y = 15,即 x – y = 5 ④;
② – ③ 得:x + 2y = 11 ⑤;
⑤–④:得 3y = 6,即 y = 2;
所以原方程组的解为:
将 y = 2 代入 ④ 得:x = 7;
把 x = 7,y = 2 代入 ③ 得:z = – 2;
(3)
①②
③
解:① + ② 得:x + y = 2 ④;
2. 解方程组:
①②
③
① + ③ 得:7x – 2y = 32 ⑤;
所以原方程组的解为:
把 x = 4,y = – 2 代入 ② 得:z = 0;
联立 ④ ⑤ 得:
④
⑤
解得:
【当堂检测】
3.关于x、y的方程组 的解是 ,求 m2 – n2 的值.
所以 m2 – n2 = 4 – 9 = – 5.
【当堂检测】
解:已知:关于x、y的方程组 的解是 ;
把 x = 1,y = 1 代入上述方程组可得:
解得:m = 2,n = 3;
四、典型例题
(三)、利用一次方程组解决实际问题
例3.某校订购了A、B两种笔记本,A种笔记本单价为28元,B种单价为24元,若B种笔记本的订购数量比A种笔记本的2倍少20个,并且订购两种笔记本共用了2560元.问该校分别订购了A、B两种笔记本各多少个?
分析:根据“B种笔记本的订购数量比A种笔记本的2倍少20个”和“两种笔记本共用了2560元”列方程组求解.
等量关系: B种笔记本的订购数量 = A种笔记本的数量×2 – 20;
B种笔记本费用 + A种笔记本费用 = 2560;
四、典型例题
解:设该校订购了A种笔记本 x 个,B种笔记本 y 个;
方程组的解:
答:该校订购了A种笔记本40个,B种笔记本60个.
根据题意,得:
①
②
把 ① 代入 ② 得:76x = 3040;
解得:x = 40;
把 x = 40 代入 ① 得:y = 60;
【当堂检测】
4. 某酒店客房有三人间、双人间客房,收费数据如表所示:
普通(元/间/天) 豪华(元/间/天)
三人间 150 300
双人间 140 400
为吸引游客,实行团体入住五折优惠措施,一个 50 人的旅游团优惠期间到该酒店入住,住了一些三人普通间和双人普通间客房,若每间客房正好住满,且一天共花去住宿费 1510 元,则旅游团住了三人普通间和双人普通间客房多少间?
【当堂检测】
普通(元/间/天) 豪华(元/间/天)
三人间 150 300
双人间 140 400
解:设三人普通间共住了 x 人,则双人普通间共住了 y 人;
解得:
三人间: (间) 双人间: (间)
根据题意得:
答:旅游团住了三人普通间客房 8 间,双人普通间客房 13 间.
5.甲、乙、丙三种商品,若买甲4件,乙5件,丙2件,共用69元;若买甲5件,乙6件,丙1件,共用84元.问买甲2件,乙3件,丙4件,共需要多少元?
解:设三种商品甲、乙、丙的单价分别是a、b、c元;
①
②
可得方程组
① × 3 – ② × 2 得:
2a + 3b + 4c = 39(元)
答:买甲2件,乙3件,丙4件,共需要39元.
【当堂检测】
五、课堂总结
代入法
加减法
实际应用
三元一次方程组
二元一次方程组
二元一次方程
解法
包含
应用
拓展
