第六章 复习课 课件 22张PPT 2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第六章 复习课 课件 22张PPT 2023-2024学年初中数学人教版七年级下册 |  | |
| 格式 | ppt | ||
| 文件大小 | 836.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 08:54:24 | ||
图片预览






文档简介
(共22张PPT)
第 6 章 实数
复习课
1.掌握平方根、立方根的概念和相关运算;
一、学习目标
3.类比有理数,掌握实数的运算法则.
2.知道无理数的概念和实数的分类,知道实数和数轴上的点一一
对应的关系;
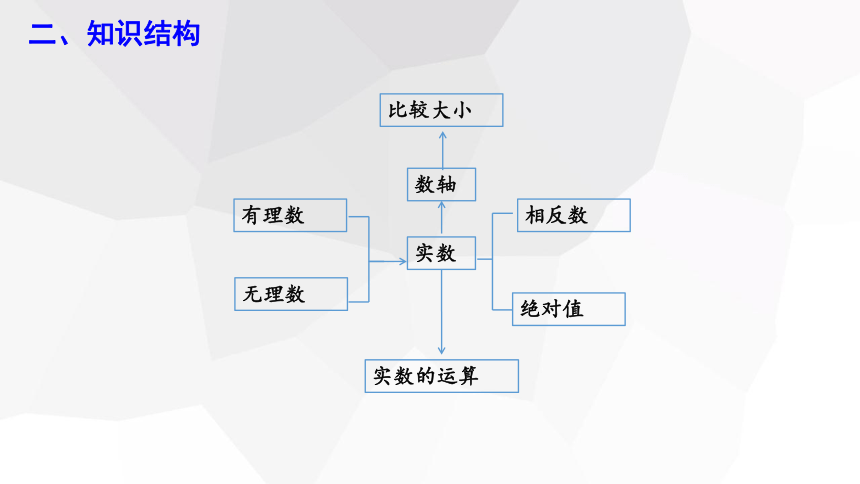
二、知识结构
有理数
无理数
比较大小
数轴
实数
相反数
绝对值
实数的运算
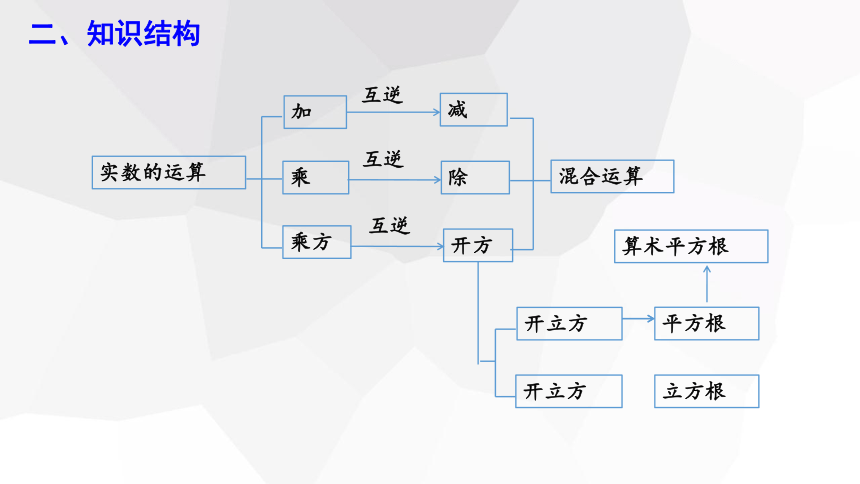
二、知识结构
实数的运算
加
乘
乘方
互逆
互逆
互逆
减
除
开方
混合运算
开立方
开立方
平方根
立方根
算术平方根
三、知识梳理
1.平方根相关概念及性质
如果一个数的平方等于a,那么这个数就叫做a的平方根,也叫二次方根.
a的正平方根记作 ,a的负平方根记作 .
a的正平方根 叫做a的算术平方根.
求一个数的平方根的运算叫做开平方.
(1)一个正数的平方根有两个,并且这两个数是相反数;
(2)0平方根为0;
(3)负数没有平方根.
性质:
三、知识梳理
2.立方根相关概念及性质
一般地,如果一个数 x 的立方等于a,即 x3=a,那么这个数 x 就叫做
a 的立方根,也叫作三次方根.
求一个数的立方根的运算叫做开立方.
记作 ,读作“三次根号a”,其中a叫被开方数,3叫做根指数.
性质:
(1)正数只有一个立方根,且立方根也是正数;
(2) 0只有一个立方根,它是0本身;
(3)负数只有一个立方根,且立方根也是负数.
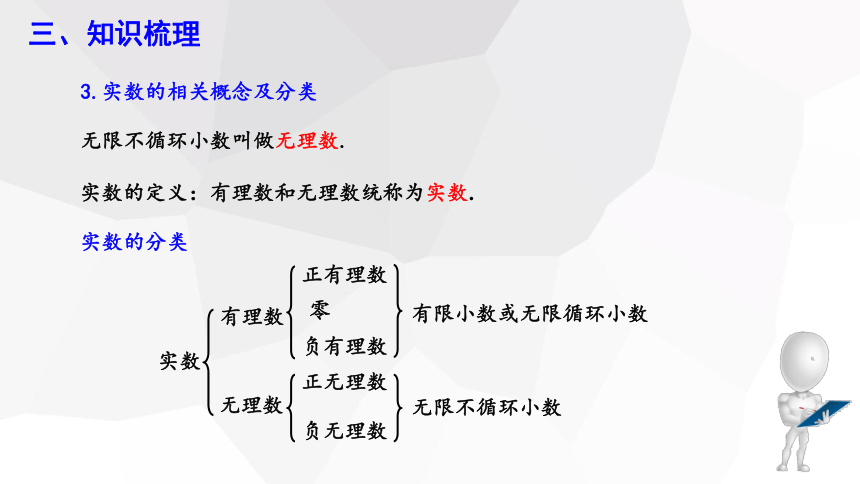
3.实数的相关概念及分类
三、知识梳理
实数的分类
无限不循环小数叫做无理数.
实数的定义:有理数和无理数统称为实数.
有理数
无理数
实数
正无理数
负无理数
正有理数
负有理数
零
有限小数或无限循环小数
无限不循环小数
三、知识梳理
4.实数与数轴之间的关系
实数和数轴上的点是一一对应的.
在数轴上,右边的点表示的数比左边的点表示的数大.
5.实数的相关性质
在实数范围内,相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样.
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且
有理数的运算法则与运算律对实数仍然适用.
三、知识梳理
6.实数的大小比较
与有理数一样,实数可以比较大小.
数轴上右边的点表示的实数比左边的点表示的实数大.
0
正实数
负实数
<
归纳:
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
四、典型例题
(一)平方根与立方根的概念与性质
例1.
(1)4是________的算术平方根;
(2)-8的立方根是________.
-2
16
解析: (1) 因为42=16,所以4是16的算术平方根;
(2) 因为(-2)3=-8,所以-8的立方根为-2.
四、典型例题
例2.如果一个正数的两个平方根分别是a+6和2a-15,求这个正数的值.
解:根据题意得:a+6+(2a-15)=0,
解得a=3,
则这个数是(a+6)2=(3+6)2=81.
四、典型例题
归纳总结:平方根、立方根的区别与联系:
区别:(1)平方根用“± ”表示,根指数2可以省略不写,
立方根用“ ”表示,根指数3不能省略;
(2)正数的平方根有两个,而立方根只有一个;
(3)只有非负数才有平方根,而任意实数都有一个立方根.
联系:(1)两者都与相应的乘方运算互为逆运算;
(2)0的平方根和立方根都是0.
【当堂检测】
±8
4
1.填空
(1)64的平方根是 ,立方根是 .
(2) 的算术平方根是 .
3
注意: 本身就等于9,所以它的算术平方根是3,而不是9.
四、典型例题
(二)实数的相关概念
例3.
D
B
四、典型例题
归纳总结:常见的三种无理数:
①根号型:如 等开方开不尽的数;
②构造型:如1.21121112…等有规律但不循环的小数;
③化简后含有π的数.
四、典型例题
例4.如图,已知直径为1个单位长度的圆形纸片上的点A与数轴上表示-1的点重合,若将该圆形纸片沿数轴顺时针滚动一周(无滑动)后,点A与数轴上的点A′重合,则点A′表示的数为________.
解析:因为圆的直径为1,所以圆的周长为π,所以点A′表示的数为π-1.
π-1
四、典型例题
(三)实数的运算
解:(1)原式=3+ -1- ,
=3-1+ - ,
=2.
(2)原式=(3+1) +1-1,
=4 .
四、典型例题
归纳总结:
在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号内的,同级运算要按照从左到右的顺序进行.有理数的运算律在实数范围内仍然适用.
【当堂检测】
2.计算
(1)2×( +1)-2= ;
(2)|2- |+| -3|= .
1
四、典型例题
(四)实数的大小比较
解:
例6.比较 与 的大小.
因为 <3,
所以
所以 .
【当堂检测】
3.比较下列各组数的大小.
(1)-2.2 -2.2;
.
(2)-3 -π;
(3) 2 ;
<
>
<
解析:绝对值较大的负实数,在数轴上它离原点距离更远,所以更靠左边;而数轴上右边的点所表示的数总是大于左边的,所以绝对值较大的负实数值更小,
所以 .
(3)因为
五、课堂总结
实数
无理数的概念和形式
实数和数轴上的点一一对应
实数的相反数、倒数、绝对值
实数的运算及估算
平方根的定义及性质
算术平方根的定义及性质
立方平方根的定义及性质
第 6 章 实数
复习课
1.掌握平方根、立方根的概念和相关运算;
一、学习目标
3.类比有理数,掌握实数的运算法则.
2.知道无理数的概念和实数的分类,知道实数和数轴上的点一一
对应的关系;
二、知识结构
有理数
无理数
比较大小
数轴
实数
相反数
绝对值
实数的运算
二、知识结构
实数的运算
加
乘
乘方
互逆
互逆
互逆
减
除
开方
混合运算
开立方
开立方
平方根
立方根
算术平方根
三、知识梳理
1.平方根相关概念及性质
如果一个数的平方等于a,那么这个数就叫做a的平方根,也叫二次方根.
a的正平方根记作 ,a的负平方根记作 .
a的正平方根 叫做a的算术平方根.
求一个数的平方根的运算叫做开平方.
(1)一个正数的平方根有两个,并且这两个数是相反数;
(2)0平方根为0;
(3)负数没有平方根.
性质:
三、知识梳理
2.立方根相关概念及性质
一般地,如果一个数 x 的立方等于a,即 x3=a,那么这个数 x 就叫做
a 的立方根,也叫作三次方根.
求一个数的立方根的运算叫做开立方.
记作 ,读作“三次根号a”,其中a叫被开方数,3叫做根指数.
性质:
(1)正数只有一个立方根,且立方根也是正数;
(2) 0只有一个立方根,它是0本身;
(3)负数只有一个立方根,且立方根也是负数.
3.实数的相关概念及分类
三、知识梳理
实数的分类
无限不循环小数叫做无理数.
实数的定义:有理数和无理数统称为实数.
有理数
无理数
实数
正无理数
负无理数
正有理数
负有理数
零
有限小数或无限循环小数
无限不循环小数
三、知识梳理
4.实数与数轴之间的关系
实数和数轴上的点是一一对应的.
在数轴上,右边的点表示的数比左边的点表示的数大.
5.实数的相关性质
在实数范围内,相反数、绝对值的意义和有理数范围内的相反数、绝对值的意义完全一样.
实数和有理数一样,可以进行加、减、乘、除、乘方运算,而且
有理数的运算法则与运算律对实数仍然适用.
三、知识梳理
6.实数的大小比较
与有理数一样,实数可以比较大小.
数轴上右边的点表示的实数比左边的点表示的实数大.
0
正实数
负实数
<
归纳:
1.正数大于零,负数小于零,正数大于负数;
2.两个正数,绝对值大的数较大;
3.两个负数,绝对值大的数反而小.
与有理数一样,在实数范围内:
四、典型例题
(一)平方根与立方根的概念与性质
例1.
(1)4是________的算术平方根;
(2)-8的立方根是________.
-2
16
解析: (1) 因为42=16,所以4是16的算术平方根;
(2) 因为(-2)3=-8,所以-8的立方根为-2.
四、典型例题
例2.如果一个正数的两个平方根分别是a+6和2a-15,求这个正数的值.
解:根据题意得:a+6+(2a-15)=0,
解得a=3,
则这个数是(a+6)2=(3+6)2=81.
四、典型例题
归纳总结:平方根、立方根的区别与联系:
区别:(1)平方根用“± ”表示,根指数2可以省略不写,
立方根用“ ”表示,根指数3不能省略;
(2)正数的平方根有两个,而立方根只有一个;
(3)只有非负数才有平方根,而任意实数都有一个立方根.
联系:(1)两者都与相应的乘方运算互为逆运算;
(2)0的平方根和立方根都是0.
【当堂检测】
±8
4
1.填空
(1)64的平方根是 ,立方根是 .
(2) 的算术平方根是 .
3
注意: 本身就等于9,所以它的算术平方根是3,而不是9.
四、典型例题
(二)实数的相关概念
例3.
D
B
四、典型例题
归纳总结:常见的三种无理数:
①根号型:如 等开方开不尽的数;
②构造型:如1.21121112…等有规律但不循环的小数;
③化简后含有π的数.
四、典型例题
例4.如图,已知直径为1个单位长度的圆形纸片上的点A与数轴上表示-1的点重合,若将该圆形纸片沿数轴顺时针滚动一周(无滑动)后,点A与数轴上的点A′重合,则点A′表示的数为________.
解析:因为圆的直径为1,所以圆的周长为π,所以点A′表示的数为π-1.
π-1
四、典型例题
(三)实数的运算
解:(1)原式=3+ -1- ,
=3-1+ - ,
=2.
(2)原式=(3+1) +1-1,
=4 .
四、典型例题
归纳总结:
在进行实数运算时,和有理数运算一样,要从高级到低级,即先算乘方、开方,再算乘除,最后算加减,有括号的要先算括号内的,同级运算要按照从左到右的顺序进行.有理数的运算律在实数范围内仍然适用.
【当堂检测】
2.计算
(1)2×( +1)-2= ;
(2)|2- |+| -3|= .
1
四、典型例题
(四)实数的大小比较
解:
例6.比较 与 的大小.
因为 <3,
所以
所以 .
【当堂检测】
3.比较下列各组数的大小.
(1)-2.2 -2.2;
.
(2)-3 -π;
(3) 2 ;
<
>
<
解析:绝对值较大的负实数,在数轴上它离原点距离更远,所以更靠左边;而数轴上右边的点所表示的数总是大于左边的,所以绝对值较大的负实数值更小,
所以 .
(3)因为
五、课堂总结
实数
无理数的概念和形式
实数和数轴上的点一一对应
实数的相反数、倒数、绝对值
实数的运算及估算
平方根的定义及性质
算术平方根的定义及性质
立方平方根的定义及性质
