16.1 二次根式 第2课时 课件(共18张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 16.1 二次根式 第2课时 课件(共18张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 00:00:00 | ||
图片预览






文档简介
(共18张PPT)
第十六章 二次根式
16.1 二次根式
第2课时
一、学习目标
1.类比算术平方根的意义,掌握二次根式的平方运算
2.类比算术平方根的意义,掌握二次根式的开方运算
二、新课导入
复习回顾
1.算数平方根的概念:
2.二次根式的概念:
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.
一般地,我们把形如 的式子叫做二次根式.“ ”称为二次根号.
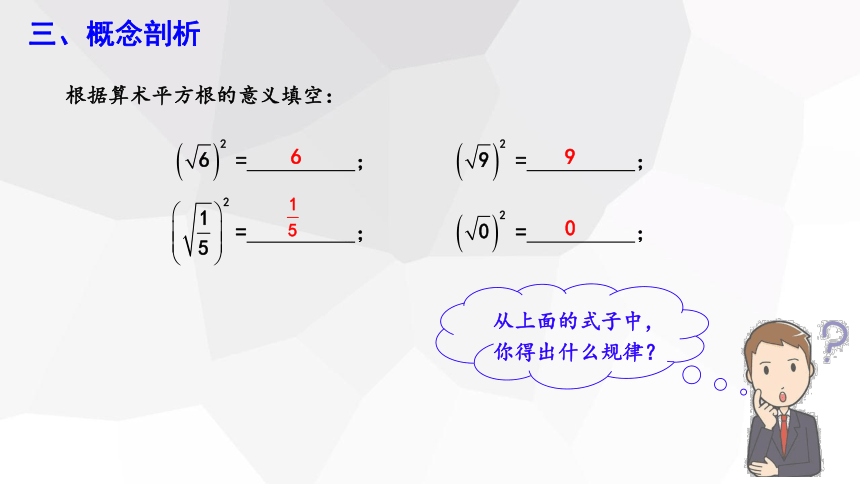
三、概念剖析
根据算术平方根的意义填空:
= ;
= ;
= ;
= ;
6
9
0
从上面的式子中,你得出什么规律?
三、概念剖析
是a的算术平方根,根据算术平方根的意义, 是一个平方等于a的非负数.因此有 .
因此,得出:
三、概念剖析
想一想:
等于什么?
分析:取a的一些值,如2,-2,3,-3,…分别计算出对应的 的值,看看有什么规律.
当a=2时,
当a=-2时,
当a=3时,
当a=-3时,
三、概念剖析
一般地,根据算术平方根的意义,有:
四、典型例题
例1.计算下列式子:
(1) ; (2) ; (3) ; (4)
解:(1) =
(2) =32× =9×5=45
(3) =
(4)
四、典型例题
例2.计算下列式子:
(1) ; (2) ; (3) ; (4)
解:(1) = =3
(2) = =4
(3) = =5
(4)
四、典型例题
总结:
回顾我们学过的式子,如5,a,a+b,-ab, ,-x3, , ,
它们都是用基本运算符号(基本运算符号包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子,我们称这样的式子为代数式.
【当堂检测】
1.下列各式中,正确的是( )
A. =-2 B. =9 C. =±3 D. =±3
D
【当堂检测】
2.计算:
(1) ; (2) ; (3) ; (4)
解:(1) =(-5)2× =25×6=150
(2) = =7
(3) =
(4) = =11
四、典型例题
例3.已知实数ab在数轴上的位置如图所示,化简:
分析:根据数轴确定a和b的取值范围,进而确定a+1、b-1和a-b的取值范围,再根据二次根式的性质和绝对值的意义化简求解.
四、典型例题
例3.已知实数ab在数轴上的位置如图所示,化简:
解:从数轴上a,b的位置关系可知-2<a<-1,1<b<2,且b>a,
故a+1<0,b-1>0.
原式=|a+1|+2|b-1|-|a-b|
=-(a+1)+2(b-1)+(a-b)
=b-3
四、典型例题
总结:
结合数轴利用二次根式的性质求值或化简,解题的关键是根据数轴判断字母的取值范围和熟练运用二次根式的性质.
【当堂检测】
3.实数a在数轴上的位置如图所示,则 化简后为( )
A.7 B.﹣7 C.2a﹣15 D.无法确定
A
【当堂检测】
4.若x<2,化简 的正确结果是 .
分析:先根据x的取值范围,判断出x-2和3-x的符号,
∵x<2,∴x-2<0,3-x>0,
=-(x-2)+(3-x)
=-x+2+3-x
=5-2x
5-2x
五、课堂总结
定义
性质
二次根式
第十六章 二次根式
16.1 二次根式
第2课时
一、学习目标
1.类比算术平方根的意义,掌握二次根式的平方运算
2.类比算术平方根的意义,掌握二次根式的开方运算
二、新课导入
复习回顾
1.算数平方根的概念:
2.二次根式的概念:
一般地,如果一个正数x的平方等于a,即x2=a,那么这个正数x叫做a的算术平方根.
一般地,我们把形如 的式子叫做二次根式.“ ”称为二次根号.
三、概念剖析
根据算术平方根的意义填空:
= ;
= ;
= ;
= ;
6
9
0
从上面的式子中,你得出什么规律?
三、概念剖析
是a的算术平方根,根据算术平方根的意义, 是一个平方等于a的非负数.因此有 .
因此,得出:
三、概念剖析
想一想:
等于什么?
分析:取a的一些值,如2,-2,3,-3,…分别计算出对应的 的值,看看有什么规律.
当a=2时,
当a=-2时,
当a=3时,
当a=-3时,
三、概念剖析
一般地,根据算术平方根的意义,有:
四、典型例题
例1.计算下列式子:
(1) ; (2) ; (3) ; (4)
解:(1) =
(2) =32× =9×5=45
(3) =
(4)
四、典型例题
例2.计算下列式子:
(1) ; (2) ; (3) ; (4)
解:(1) = =3
(2) = =4
(3) = =5
(4)
四、典型例题
总结:
回顾我们学过的式子,如5,a,a+b,-ab, ,-x3, , ,
它们都是用基本运算符号(基本运算符号包括加、减、乘、除、乘方和开方)把数或表示数的字母连接起来的式子,我们称这样的式子为代数式.
【当堂检测】
1.下列各式中,正确的是( )
A. =-2 B. =9 C. =±3 D. =±3
D
【当堂检测】
2.计算:
(1) ; (2) ; (3) ; (4)
解:(1) =(-5)2× =25×6=150
(2) = =7
(3) =
(4) = =11
四、典型例题
例3.已知实数ab在数轴上的位置如图所示,化简:
分析:根据数轴确定a和b的取值范围,进而确定a+1、b-1和a-b的取值范围,再根据二次根式的性质和绝对值的意义化简求解.
四、典型例题
例3.已知实数ab在数轴上的位置如图所示,化简:
解:从数轴上a,b的位置关系可知-2<a<-1,1<b<2,且b>a,
故a+1<0,b-1>0.
原式=|a+1|+2|b-1|-|a-b|
=-(a+1)+2(b-1)+(a-b)
=b-3
四、典型例题
总结:
结合数轴利用二次根式的性质求值或化简,解题的关键是根据数轴判断字母的取值范围和熟练运用二次根式的性质.
【当堂检测】
3.实数a在数轴上的位置如图所示,则 化简后为( )
A.7 B.﹣7 C.2a﹣15 D.无法确定
A
【当堂检测】
4.若x<2,化简 的正确结果是 .
分析:先根据x的取值范围,判断出x-2和3-x的符号,
∵x<2,∴x-2<0,3-x>0,
=-(x-2)+(3-x)
=-x+2+3-x
=5-2x
5-2x
五、课堂总结
定义
性质
二次根式
