17.1 勾股定理 课件(第2课时)14张PPT 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 17.1 勾股定理 课件(第2课时)14张PPT 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 658.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 10:16:37 | ||
图片预览




文档简介
(共14张PPT)
第十七章 勾股定理
17.1 勾股定理
第2课时
1.能从实际问题中抽象出直角三角形这一几何模型;
2.会用勾股定理解决实际问题.
一、学习目标
二、新课导入
电视的尺寸是屏幕对角线的长度.小华的爸爸买了一台29英寸(74 cm)的电视机,小华量电视机的屏幕后,发现屏幕只有58 cm长和46 cm宽.他觉得一定是售货员搞错了,你同意他的想法吗?你能解释是为什么吗?
三、典型例题
例1.一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
A
B
C
D
1 m
2 m
分析:可以看出,木板横着或竖着都不能从门框通过,只能试试斜着能否通过.门框对角线AC的长度是斜着能通过的最大长度.求出AC,再与木板的宽比较,就能知道木板能否通过.
三、典型例题
A
B
C
D
1 m
2 m
所以木板能从门框内通过.
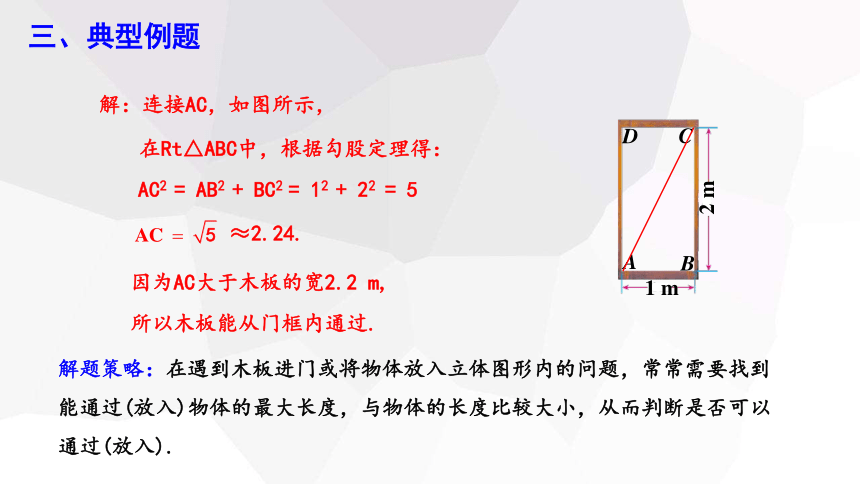
解:连接AC,如图所示,
AC2 = AB2 + BC2
≈2.24.
因为AC大于木板的宽2.2 m,
在Rt△ABC中,根据勾股定理得:
= 12 + 22
= 5
解题策略:在遇到木板进门或将物体放入立体图形内的问题,常常需要找到能通过(放入)物体的最大长度,与物体的长度比较大小,从而判断是否可以通过(放入).
三、典型例题
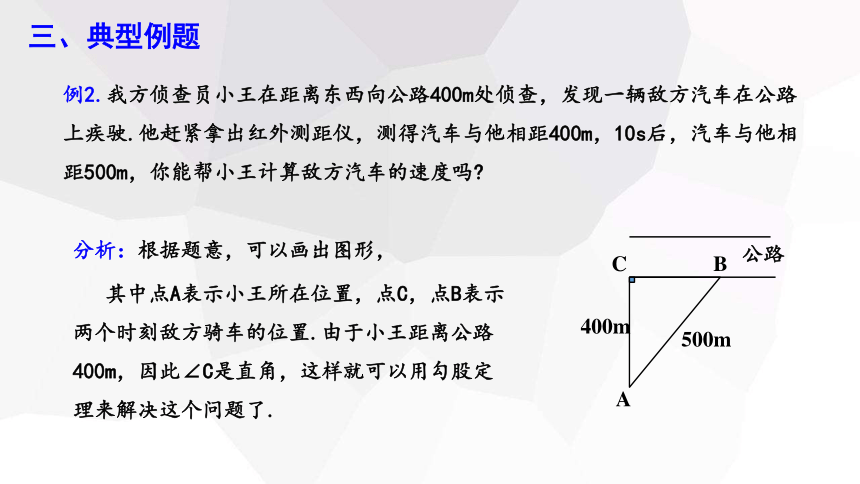
例2.我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
分析:根据题意,可以画出图形,
其中点A表示小王所在位置,点C,点B表示两个时刻敌方骑车的位置.由于小王距离公路400m,因此∠C是直角,这样就可以用勾股定理来解决这个问题了.
公路
B
C
A
400m
500m
三、典型例题
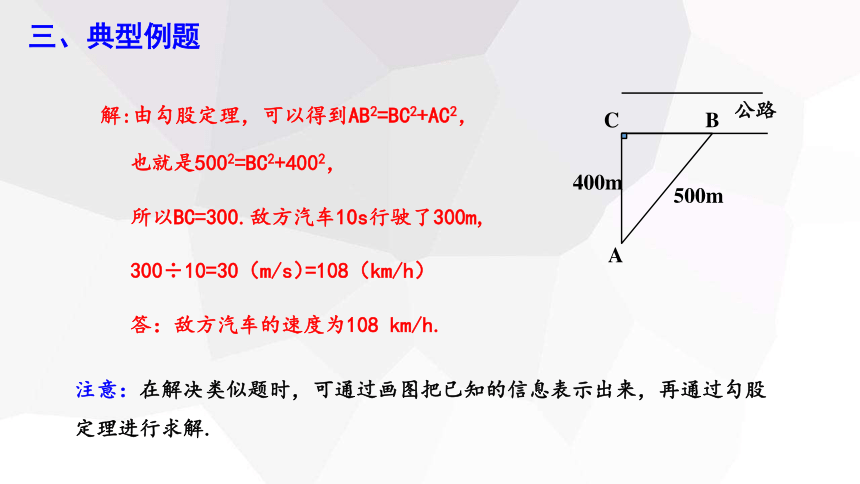
答:敌方汽车的速度为108 km/h.
解:由勾股定理,可以得到AB2=BC2+AC2,
也就是5002=BC2+4002,
所以BC=300.敌方汽车10s行驶了300m,
300÷10=30(m/s)
=108(km/h)
注意:在解决类似题时,可通过画图把已知的信息表示出来,再通过勾股定理进行求解.
公路
B
C
A
400m
500m
三、典型例题
归纳总结
在实际应用题中,求线段长度的问题可以通过建模思想,将实际问题转化为数学中直角三角形的问题,再利用勾股定理算出对应线段的长度.
【当堂检测】
1.如图,是一长方形公园,如果某人从景点A走到景点D,则至少要走( )米.
A. 15 B. 17 C. 19 D. 21
A
B
C
D
8米
15米
B
【当堂检测】
D
2.如图所示,一只蚂蚁沿棱长为a的正方体表面从顶点A爬到顶点B,则它走过的最短路程为( )
A. B. C. 3a D.
【当堂检测】
3.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
答:梯脚与墙的距离是0.7米.
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2 =2.52-2.42 =0.49,
所以BC=0.7.
【当堂检测】
4.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4 km处,过了15 s,飞机距离这个男孩头顶5 km.这一过程中飞机飞过的距离是多少千米?
解:在Rt△ABC中,
答:飞机飞过的距离是3 km.
4
5
5
4
C
B
A
∵BC>0
∴BC=3(km)
BC2=52-42=9
【当堂检测】
5.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?
小汽车
小汽车
观测点
A
B
C
答:这辆小汽车超速了.
解:在Rt△ABC中,根据勾股定理,得:
BC2=AC2-AB2 =502-302 =1600,
所以BC=40(m).
可得速度是40÷2=20(m/s)=72(km/h)
>70(km/h).
四、课堂总结
在实际应用题中,求线段长度的问题可以通过建模思想,将实际问题转化为数学中直角三角形的问题,再利用勾股定理算出对应线段的长度.
勾股定理的实际应用:
第十七章 勾股定理
17.1 勾股定理
第2课时
1.能从实际问题中抽象出直角三角形这一几何模型;
2.会用勾股定理解决实际问题.
一、学习目标
二、新课导入
电视的尺寸是屏幕对角线的长度.小华的爸爸买了一台29英寸(74 cm)的电视机,小华量电视机的屏幕后,发现屏幕只有58 cm长和46 cm宽.他觉得一定是售货员搞错了,你同意他的想法吗?你能解释是为什么吗?
三、典型例题
例1.一个门框的尺寸如图所示,一块长3 m,宽2.2 m的长方形薄木板能否从门框内通过?为什么?
A
B
C
D
1 m
2 m
分析:可以看出,木板横着或竖着都不能从门框通过,只能试试斜着能否通过.门框对角线AC的长度是斜着能通过的最大长度.求出AC,再与木板的宽比较,就能知道木板能否通过.
三、典型例题
A
B
C
D
1 m
2 m
所以木板能从门框内通过.
解:连接AC,如图所示,
AC2 = AB2 + BC2
≈2.24.
因为AC大于木板的宽2.2 m,
在Rt△ABC中,根据勾股定理得:
= 12 + 22
= 5
解题策略:在遇到木板进门或将物体放入立体图形内的问题,常常需要找到能通过(放入)物体的最大长度,与物体的长度比较大小,从而判断是否可以通过(放入).
三、典型例题
例2.我方侦查员小王在距离东西向公路400m处侦查,发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪,测得汽车与他相距400m,10s后,汽车与他相距500m,你能帮小王计算敌方汽车的速度吗
分析:根据题意,可以画出图形,
其中点A表示小王所在位置,点C,点B表示两个时刻敌方骑车的位置.由于小王距离公路400m,因此∠C是直角,这样就可以用勾股定理来解决这个问题了.
公路
B
C
A
400m
500m
三、典型例题
答:敌方汽车的速度为108 km/h.
解:由勾股定理,可以得到AB2=BC2+AC2,
也就是5002=BC2+4002,
所以BC=300.敌方汽车10s行驶了300m,
300÷10=30(m/s)
=108(km/h)
注意:在解决类似题时,可通过画图把已知的信息表示出来,再通过勾股定理进行求解.
公路
B
C
A
400m
500m
三、典型例题
归纳总结
在实际应用题中,求线段长度的问题可以通过建模思想,将实际问题转化为数学中直角三角形的问题,再利用勾股定理算出对应线段的长度.
【当堂检测】
1.如图,是一长方形公园,如果某人从景点A走到景点D,则至少要走( )米.
A. 15 B. 17 C. 19 D. 21
A
B
C
D
8米
15米
B
【当堂检测】
D
2.如图所示,一只蚂蚁沿棱长为a的正方体表面从顶点A爬到顶点B,则它走过的最短路程为( )
A. B. C. 3a D.
【当堂检测】
3.一高为2.5米的木梯,架在高为2.4米的墙上(如图),这时梯脚与墙的距离是多少?
A
B
C
答:梯脚与墙的距离是0.7米.
解:在Rt△ABC中,根据勾股定理,得:
BC2=AB2-AC2 =2.52-2.42 =0.49,
所以BC=0.7.
【当堂检测】
4.飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4 km处,过了15 s,飞机距离这个男孩头顶5 km.这一过程中飞机飞过的距离是多少千米?
解:在Rt△ABC中,
答:飞机飞过的距离是3 km.
4
5
5
4
C
B
A
∵BC>0
∴BC=3(km)
BC2=52-42=9
【当堂检测】
5.“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30m处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?
小汽车
小汽车
观测点
A
B
C
答:这辆小汽车超速了.
解:在Rt△ABC中,根据勾股定理,得:
BC2=AC2-AB2 =502-302 =1600,
所以BC=40(m).
可得速度是40÷2=20(m/s)=72(km/h)
>70(km/h).
四、课堂总结
在实际应用题中,求线段长度的问题可以通过建模思想,将实际问题转化为数学中直角三角形的问题,再利用勾股定理算出对应线段的长度.
勾股定理的实际应用:
