17.2 勾股定理的逆定理 课件(共17张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 17.2 勾股定理的逆定理 课件(共17张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 665.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-27 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
第十七章 勾股定理
17.2 勾股定理的逆定理
1.能知道勾股定理的逆定理,能根据该定理判断一个三角形是不是直角三角形
2.能理解原命题、逆命题、逆定理的概念
3.知道勾股数的概念,并能熟记一些勾股数
4.能应用勾股定理及其逆定理解决生活中的实际问题
一、学习目标
1.勾股定理的内容是什么
复习回顾
如果直角三角形的两条直角边长分别为a,b,斜边为c,
那么a2+b2=c2.
B
C
A
b
c
a
2.求以线段a、b为直角边的直角三角形的斜边c的长:
① a=3,b=4;
② a=2.5,b=6;
③ a=4,b=7.5.
c=5
c=6.5
c=8.5
二、新课导入
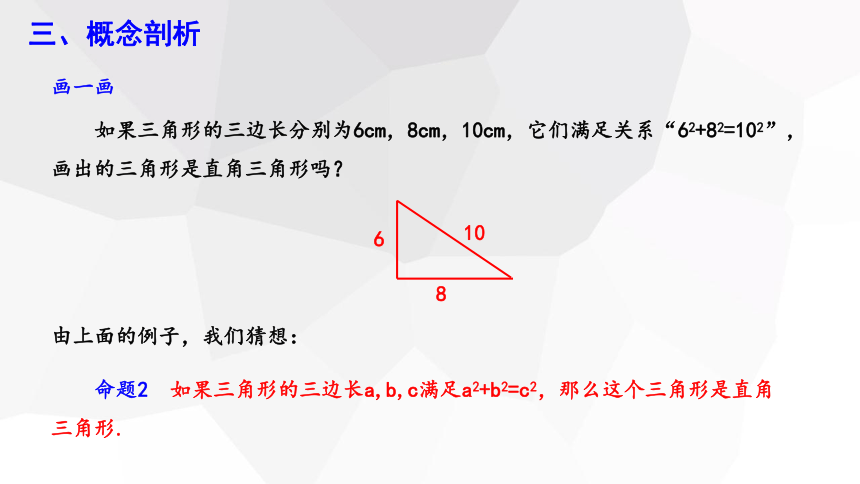
如果三角形的三边长分别为6cm,8cm,10cm,它们满足关系“62+82=102”,画出的三角形是直角三角形吗?
画一画
6
8
10
由上面的例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
三、概念剖析
证明猜想
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
A
B
C
a
b
c
证明:作Rt△A'B'C',使∠C'=90°,A'C'=b,B'C'=a,
则A'B'2=B'C'2+A'C'2=a2+b2
∵a2 + b2 = c2,
∴A'B'2 = c2,A'B' = c
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS),
∴∠C=∠C'=90°,即△ABC是直角三角形.
三、概念剖析
得出结论
勾股定理的逆定理:
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
A
C
B
a
b
c
拓展知识
能够成为直角三角形三条边长的三个正整数,称为勾股数.
三、概念剖析
想一想
勾股定理和勾股定理的逆定理之间有什么不同?
题设和结论相反.
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.
得出概念:
如果把其中一个命题叫做原命题,
那么另一个命题叫做它的逆命题.
三、概念剖析
例1.判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c=15.
分析:根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
解:(1)∵82+152=
64+225
=289,
172=289,
∴82+152=172,
根据勾股定理的逆定理可知这个三角形是直角三角形.
典型例题
例1.判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c=15.
解:(2)∵132+142=
169+196
=365,
152=225,
∴132+142≠152,
根据勾股定理,可知这个三角形不是直角三角形.
典型例题
例2.下列各组数中,不是勾股数的是( )
A.12,16,20 B.8,15,17
C.32,42,52 D.5,12,13
C
解析:A、122+162=202,能构成直角三角形,是正整数,故是勾股数;
B、82+152=172,能构成直角三角形,是正整数,故是勾股数;
C、92+162≠252,不能构成直角三角形,故不是勾股数;
D、52+122=132,能构成直角三角形,是正整数,故是勾股数;
典型例题
归纳总结
判断一组数是否为勾股数需要满足下列两个条件:
(1)是否符合a2+b2=c2;
(2)它们是否是正整数.
典型例题
1.①7,24,25;②8,15,19;③0.6,0.8,1.0;④3n,4n,5n(n>1,且为自然数).
上面各组数中,勾股数的组数是有( )
A.1 B.2 C.3 D.4
C
【当堂检测】
2.判断满足下列条件的三角形是否是直角三角形:
在△ABC中,AC=10,AB=24,BC=26.
解:∵102+242=
100+576
=676,
262=676,
∴102+242=262,
根据勾股定理的逆定理可知这个三角形是直角三角形.
【当堂检测】
例3.一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,这个零件符合要求吗
D
A
B
C
图1
D
A
B
C
4
3
5
13
12
图2
典型例题
所以△BCD 是直角三角形,∠DBC是直角.
解:在△ABD中,
D
A
B
C
4
3
5
13
12
所以△ABD 是直角三角形,∠A是直角.
在△BCD中,
因此,这个零件符合要求.
典型例题
3.有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若沿对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
∴△ACD也为直角三角形.
解:都是直角三角形.理由如下:
连接AC.在△ABC中,
∵∠B=90°,∴△ABC为直角三角形;
∴AC2=AB2+BC2=8,
又∵AD2+AC2=1+8=9,且DC2=9,
∴AC2+AD2=DC2,
【当堂检测】
1.勾股定理的逆定理:
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
A
C
B
a
b
c
3.原命题和逆命题:
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.
如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
2.能够成为直角三角形三条边长的三个正整数,称为勾股数.
四、课堂总结
第十七章 勾股定理
17.2 勾股定理的逆定理
1.能知道勾股定理的逆定理,能根据该定理判断一个三角形是不是直角三角形
2.能理解原命题、逆命题、逆定理的概念
3.知道勾股数的概念,并能熟记一些勾股数
4.能应用勾股定理及其逆定理解决生活中的实际问题
一、学习目标
1.勾股定理的内容是什么
复习回顾
如果直角三角形的两条直角边长分别为a,b,斜边为c,
那么a2+b2=c2.
B
C
A
b
c
a
2.求以线段a、b为直角边的直角三角形的斜边c的长:
① a=3,b=4;
② a=2.5,b=6;
③ a=4,b=7.5.
c=5
c=6.5
c=8.5
二、新课导入
如果三角形的三边长分别为6cm,8cm,10cm,它们满足关系“62+82=102”,画出的三角形是直角三角形吗?
画一画
6
8
10
由上面的例子,我们猜想:
命题2 如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
三、概念剖析
证明猜想
已知:如图,△ABC的三边长a,b,c,满足a2+b2=c2.
求证:△ABC是直角三角形.
A
B
C
a
b
c
证明:作Rt△A'B'C',使∠C'=90°,A'C'=b,B'C'=a,
则A'B'2=B'C'2+A'C'2=a2+b2
∵a2 + b2 = c2,
∴A'B'2 = c2,A'B' = c
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SSS),
∴∠C=∠C'=90°,即△ABC是直角三角形.
三、概念剖析
得出结论
勾股定理的逆定理:
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
A
C
B
a
b
c
拓展知识
能够成为直角三角形三条边长的三个正整数,称为勾股数.
三、概念剖析
想一想
勾股定理和勾股定理的逆定理之间有什么不同?
题设和结论相反.
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.
得出概念:
如果把其中一个命题叫做原命题,
那么另一个命题叫做它的逆命题.
三、概念剖析
例1.判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c=15.
分析:根据勾股定理及其逆定理,判断一个三角形是不是直角三角形,只要看两条较小边长的平方和是否等于最大边长的平方.
解:(1)∵82+152=
64+225
=289,
172=289,
∴82+152=172,
根据勾股定理的逆定理可知这个三角形是直角三角形.
典型例题
例1.判断由线段a,b,c组成的三角形是不是直角三角形:
(1)a=15,b=8,c=17;
(2)a=13,b=14,c=15.
解:(2)∵132+142=
169+196
=365,
152=225,
∴132+142≠152,
根据勾股定理,可知这个三角形不是直角三角形.
典型例题
例2.下列各组数中,不是勾股数的是( )
A.12,16,20 B.8,15,17
C.32,42,52 D.5,12,13
C
解析:A、122+162=202,能构成直角三角形,是正整数,故是勾股数;
B、82+152=172,能构成直角三角形,是正整数,故是勾股数;
C、92+162≠252,不能构成直角三角形,故不是勾股数;
D、52+122=132,能构成直角三角形,是正整数,故是勾股数;
典型例题
归纳总结
判断一组数是否为勾股数需要满足下列两个条件:
(1)是否符合a2+b2=c2;
(2)它们是否是正整数.
典型例题
1.①7,24,25;②8,15,19;③0.6,0.8,1.0;④3n,4n,5n(n>1,且为自然数).
上面各组数中,勾股数的组数是有( )
A.1 B.2 C.3 D.4
C
【当堂检测】
2.判断满足下列条件的三角形是否是直角三角形:
在△ABC中,AC=10,AB=24,BC=26.
解:∵102+242=
100+576
=676,
262=676,
∴102+242=262,
根据勾股定理的逆定理可知这个三角形是直角三角形.
【当堂检测】
例3.一个零件的形状如图1所示,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边的尺寸如图2所示,这个零件符合要求吗
D
A
B
C
图1
D
A
B
C
4
3
5
13
12
图2
典型例题
所以△BCD 是直角三角形,∠DBC是直角.
解:在△ABD中,
D
A
B
C
4
3
5
13
12
所以△ABD 是直角三角形,∠A是直角.
在△BCD中,
因此,这个零件符合要求.
典型例题
3.有一块薄铁皮ABCD,∠B=90°,各边的尺寸如图所示,若沿对角线AC剪开,得到的两块都是“直角三角形”形状吗?为什么?
∴△ACD也为直角三角形.
解:都是直角三角形.理由如下:
连接AC.在△ABC中,
∵∠B=90°,∴△ABC为直角三角形;
∴AC2=AB2+BC2=8,
又∵AD2+AC2=1+8=9,且DC2=9,
∴AC2+AD2=DC2,
【当堂检测】
1.勾股定理的逆定理:
如果三角形的三边长a 、b 、c满足a2+b2=c2,那么这个三角形是直角三角形.
A
C
B
a
b
c
3.原命题和逆命题:
两个命题的题设与结论正好相反,像这样的两个命题叫做互逆命题.
如果把其中一个命题叫做原命题,那么另一个命题叫做它的逆命题.
2.能够成为直角三角形三条边长的三个正整数,称为勾股数.
四、课堂总结
