18.1.2 平行四边形的判定 第1课时 课件(共18张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 18.1.2 平行四边形的判定 第1课时 课件(共18张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 10:49:35 | ||
图片预览




文档简介
(共18张PPT)
第十八章 平行四边形
18.1.2 平行四边形的判定
第1课时
1.经历平行四边形判定定理的猜想与证明过程.
2.能掌握并灵活运用四个不同的判定定理.
一、学习目标
二、新课导入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
思考:在数学中,我们要怎么确保一个四边形是否是平行四边形呢?
三、概念剖析
思考:我们知道,平行四边形的对边相等、对角相等、对角线互相平分.你能说一说这些性质的逆命题吗?
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
我们得到的这些逆命题是否都成立呢?
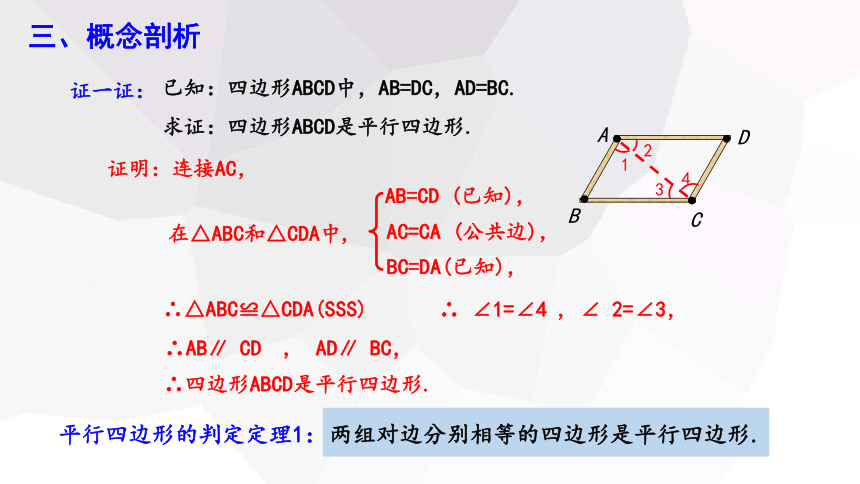
证一证:
已知:四边形ABCD中,AB=DC,AD=BC.
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:连接AC,
1
4
2
3
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴ ∠1=∠4 , ∠ 2=∠3,
∴AB∥ CD , AD∥ BC,
∴四边形ABCD是平行四边形.
三、概念剖析
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
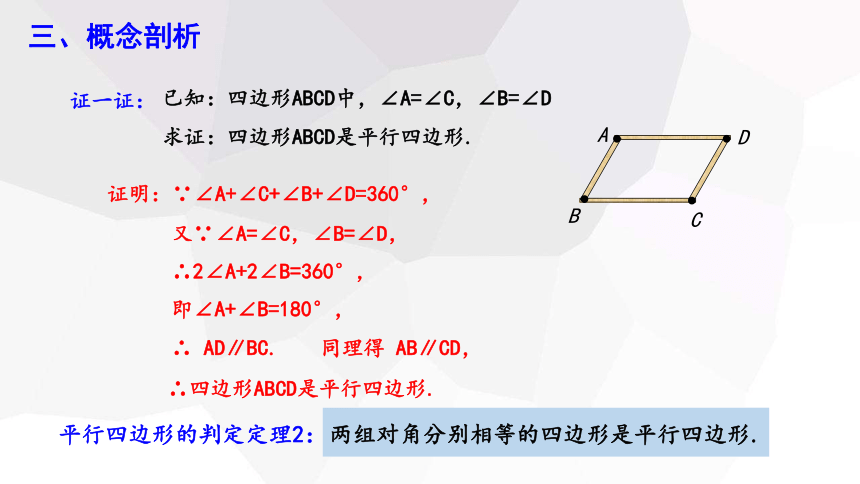
证一证:
已知:四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:∵∠A+∠C+∠B+∠D=360°,
又∵∠A=∠C,∠B=∠D,
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴ AD∥BC.
∴四边形ABCD是平行四边形.
三、概念剖析
同理得 AB∥CD,
平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形.
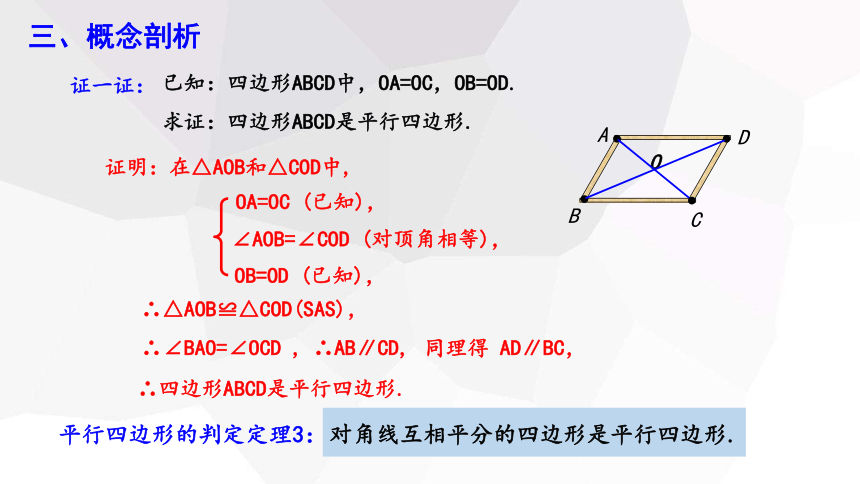
证一证:
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:在△AOB和△COD中,
∴△AOB≌△COD(SAS),
∴∠BAO=∠OCD ,
∴四边形ABCD是平行四边形.
三、概念剖析
∴AB∥CD,
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形.
O
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
同理得 AD∥BC,
三、概念剖析
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
例1.如图,□ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
典型例题
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
(对角线互相平分的四边形的平行四边形)
B
O
D
A
C
E
F
分析:首先利用平行四边形的性质,得出对角线互相平分,进而得出EO=FO,BO=DO,即可对四边形BFDE进行判定.
【当堂检测】
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
【当堂检测】
2.如图,在四边形ABCD中,
(1)如果∠A:∠B:∠ C:∠D=a:b:a:b(a,b为正数),那么四边形ABCD是
.
(2)如果AD=6cm,AB=4cm,那么当BC=_______cm,CD=_____cm时,四边形ABCD为平行四边形.
B
D
A
C
平行四边形
6
4
【当堂检测】
3.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
证明:在平行四边形ABCD中,
∠A=∠C,AD=BC,
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.
三、概念剖析
思考:我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
证一证:
四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
∴BC=DA .
∴四边形ABCD是平行四边形.
又∵AB=CD,
A
B
C
D
2
1
AB=CD,
AC=CA,
∠1=∠2,
平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形.
三、概念剖析
例2.如图,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
典型例题
分析:由垂线得到∠EAD=∠FCB=90°,根据AAS可证明Rt△AED≌Rt△CFB,得到AD=BC,根据平行四边形判定定理4即可判定.
例2.如图,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
典型例题
证明:∵AE⊥AD,CF⊥BC,
∵AD∥BC,
∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,
∴Rt△AED≌Rt△CFB(AAS).
∵AD∥BC,
∴四边形ABCD是平行四边形.(一组对边平行且相等的四边形是平行四边形)
【当堂检测】
4.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC,EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
A
B
C
D
E
F
四、课堂总结
平行四边形的判定:
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
第十八章 平行四边形
18.1.2 平行四边形的判定
第1课时
1.经历平行四边形判定定理的猜想与证明过程.
2.能掌握并灵活运用四个不同的判定定理.
一、学习目标
二、新课导入
数学来源于生活,高铁被外媒誉为我国新四大发明之一,我们知道铁路的两条直铺的铁轨互相平行,那么铁路工人是怎样的确保它们平行的呢?
思考:在数学中,我们要怎么确保一个四边形是否是平行四边形呢?
三、概念剖析
思考:我们知道,平行四边形的对边相等、对角相等、对角线互相平分.你能说一说这些性质的逆命题吗?
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形.
我们得到的这些逆命题是否都成立呢?
证一证:
已知:四边形ABCD中,AB=DC,AD=BC.
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:连接AC,
1
4
2
3
在△ABC和△CDA中,
∴△ABC≌△CDA(SSS)
AB=CD (已知),
BC=DA(已知),
AC=CA (公共边),
∴ ∠1=∠4 , ∠ 2=∠3,
∴AB∥ CD , AD∥ BC,
∴四边形ABCD是平行四边形.
三、概念剖析
平行四边形的判定定理1:
两组对边分别相等的四边形是平行四边形.
证一证:
已知:四边形ABCD中,∠A=∠C,∠B=∠D
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:∵∠A+∠C+∠B+∠D=360°,
又∵∠A=∠C,∠B=∠D,
∴2∠A+2∠B=360°,
即∠A+∠B=180°,
∴ AD∥BC.
∴四边形ABCD是平行四边形.
三、概念剖析
同理得 AB∥CD,
平行四边形的判定定理2:
两组对角分别相等的四边形是平行四边形.
证一证:
已知:四边形ABCD中,OA=OC,OB=OD.
求证:四边形ABCD是平行四边形.
A
B
C
D
证明:在△AOB和△COD中,
∴△AOB≌△COD(SAS),
∴∠BAO=∠OCD ,
∴四边形ABCD是平行四边形.
三、概念剖析
∴AB∥CD,
平行四边形的判定定理3:
对角线互相平分的四边形是平行四边形.
O
OA=OC (已知),
OB=OD (已知),
∠AOB=∠COD (对顶角相等),
同理得 AD∥BC,
三、概念剖析
平行四边形的判定定理:
两组对边分别相等的四边形是平行四边形.
两组对角分别相等的四边形是平行四边形.
对角线互相平分的四边形是平行四边形.
例1.如图,□ABCD的对角线AC,BD相交于点O,E,F是AC上的两点,并且AE=CF.求证:四边形BFDE是平行四边形.
典型例题
证明:∵四边形ABCD是平行四边形,
∴ AO=CO,BO=DO.
∵AE=CF ,
∴ AO-AE=CO-CF,即EO=OF.
又∵BO=DO,
∴四边形BFDE是平行四边形.
(对角线互相平分的四边形的平行四边形)
B
O
D
A
C
E
F
分析:首先利用平行四边形的性质,得出对角线互相平分,进而得出EO=FO,BO=DO,即可对四边形BFDE进行判定.
【当堂检测】
1.如图,四边形ABCD的对角线交于点O,下列哪组条件不能判断四边形ABCD是平行四边形( )
A.OA=OC,OB=OD
B.AB=CD,AO=CO
C.AB=CD,AD=BC
D.∠BAD=∠BCD,AB∥CD
B
O
D
A
C
B
【当堂检测】
2.如图,在四边形ABCD中,
(1)如果∠A:∠B:∠ C:∠D=a:b:a:b(a,b为正数),那么四边形ABCD是
.
(2)如果AD=6cm,AB=4cm,那么当BC=_______cm,CD=_____cm时,四边形ABCD为平行四边形.
B
D
A
C
平行四边形
6
4
【当堂检测】
3.如图,已知E,F,G,H分别是 ABCD的边AB,BC,CD,DA上的点,且AE=CG,BF=DH.求证:四边形EFGH是平行四边形.
证明:在平行四边形ABCD中,
∠A=∠C,AD=BC,
又∵BF=DH,
∴AH=CF.
又∵AE=CG,
∴△AEH≌△CGF(SAS),
∴EH=GF.
同理得△BEF≌△DGH(SAS),
∴GH=EF,
∴四边形EFGH是平行四边形.
三、概念剖析
思考:我们知道,如果一个四边形是平行四边形,那么它的任意一组对边平行且相等.反过来,一组对边平行且相等的四边形是平行四边形吗?
证一证:
四边形ABCD中,AB=CD且AB∥CD,
求证:四边形ABCD是平行四边形.
证明:连接AC.
∵AB∥CD, ∴∠1=∠2.
在△ABC和△CDA中,
∴△ABC≌△CDA(SAS),
∴BC=DA .
∴四边形ABCD是平行四边形.
又∵AB=CD,
A
B
C
D
2
1
AB=CD,
AC=CA,
∠1=∠2,
平行四边形的判定定理4:
一组对边平行且相等的四边形是平行四边形.
三、概念剖析
例2.如图,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
典型例题
分析:由垂线得到∠EAD=∠FCB=90°,根据AAS可证明Rt△AED≌Rt△CFB,得到AD=BC,根据平行四边形判定定理4即可判定.
例2.如图,在四边形ABCD中,AD∥BC,AE⊥AD交BD于点E,CF⊥BC交BD于点F,且AE=CF.求证:四边形ABCD是平行四边形.
典型例题
证明:∵AE⊥AD,CF⊥BC,
∵AD∥BC,
∴∠ADE=∠CBF,
在Rt△AED和Rt△CFB中,
∴Rt△AED≌Rt△CFB(AAS).
∵AD∥BC,
∴四边形ABCD是平行四边形.(一组对边平行且相等的四边形是平行四边形)
【当堂检测】
4.四边形AEFD和EBCF都是平行四边形,求证:四边形ABCD 是平行四边形.
证明:∵四边形AEFD和EBCF都是平行四边形,
∴AD∥ EF,AD=EF,
EF∥ BC,EF=BC.
∴AD∥ BC,AD=BC.
∴四边形ABCD是平行四边形.
A
B
C
D
E
F
四、课堂总结
平行四边形的判定:
两组对边分别相等的四边形是平行四边形;
两组对角分别相等的四边形是平行四边形;
对角线互相平分的四边形是平行四边形;
一组对边平行且相等的四边形是平行四边形.
