18.2.2 菱形 第2课时 课件(共17张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 18.2.2 菱形 第2课时 课件(共17张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 686.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 11:26:29 | ||
图片预览






文档简介
(共17张PPT)
第十八章 平行四边形
18.2.2 菱形
第2课时
1.能利用菱形的定义来判定一个四边形为菱形
2.能探究菱形的判定定理,会判定一个四边形为菱形
3.能解决与菱形相关的简单几何问题
一、学习目标
二、新课导入
那么怎样判断一个四边形是否是菱形呢
生活中很多服装设计者在设计服装的时候,往往青睐于菱形图案的设计.这是因为菱形的特殊因素能给人一种舒服的感觉.
三、概念剖析
由菱形的定义可知,有一组邻边相等的平行四边形是菱形.除此之外,还有没有其他判定方法呢?
思考:我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
三、概念剖析
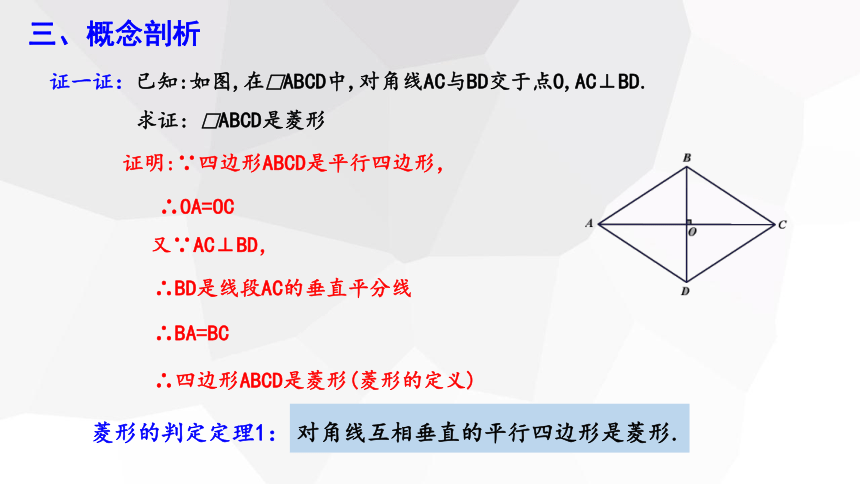
证明:∵四边形ABCD是平行四边形,
∴OA=OC
又∵AC⊥BD,
∴BD是线段AC的垂直平分线
∴BA=BC
∴四边形ABCD是菱形(菱形的定义)
菱形的判定定理1:
对角线互相垂直的平行四边形是菱形.
证一证:已知:如图,在□ABCD中,对角线AC与BD交于点O,AC⊥BD.
求证: □ABCD是菱形
典型例题
例1.如图,在 ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.求证:四边形AFBE是菱形.
分析:由平行四边形的性质得出AD∥BC,得出∠AEG=∠BFG,由AAS证明△AGE≌△BGF,得出AE=BF,由AD∥BC,可证四边形AFBE是平行四边形,由EF⊥AB,即可得出结论.
典型例题
例1.如图,在 ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.求证:四边形AFBE是菱形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AD∥FC
∴∠AEG=∠BFG,
∵EF垂直平分AB,
∴AG=BG,且∠AEG=∠BFG,∠AGE=∠BGF
∴△AGE≌△BGF(AAS);
∴AE=BF,
∵AD∥FC,
∴四边形AFBE是平行四边形,
又∵EF⊥AB,
∴四边形AFBE是菱形.(对角线互相垂直的平行四边形是菱形)
1.如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证:四边形ABCD是菱形.
【当堂检测】
A
B
C
D
O
证明:∵OA=4,OB=3,AB=5,
∴ AB =OA +OB ,
∴△AOB是直角三角形,即AC⊥BD,
∴四边形ABCD是菱形.
三、概念剖析
思考:前面的研究中我们知道菱形的四条边相等,反过来,四条边相等的四边形是菱形吗?
证一证:已知:如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
证明:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形(菱形的定义)
菱形的判定定理2:
四条边相等的四边形是菱形.
例2.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
典型例题
分析:根据平移的性质可得CF=AD,DF=AC,再在Rt△ABC中利用勾股定理求出AC的长,最后根据四条边都相等的四边形是菱形得到结论.
例2.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
典型例题
证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.(四条边相等的四边形是菱形)
∴AC=
【当堂检测】
2.如图,△ABC是等腰三角形,把它沿底边BC翻折后,得到△DBC,则四边形ABDC为 ,理由是 .
菱形
四条边相等的四边形是菱形
【当堂检测】
3.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,AF⊥BC.
求证:四边形ADFE是菱形.
证明:∵AF⊥BC,点D,E,F分别是AB,AC,BC的中点,
∴DF=AD=EF=AE,
∴四边形ADFE是菱形.
∴AB=AC,DF= AC=AE,EF= AB=AD,
典型例题
例3.如图,在 ABCD中,AC平分∠DAB,AB=2,求 ABCD的周长.
点拨:求 ABCD的周长可先证明 ABCD是菱形.
解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,
又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,
∴平行四边形ABCD为菱形,(有一组邻边相等的平行四边形是菱形)
又∵AB=2,
∴AD∥BC,
∴AB=BC,
∴四边形ABCD的周长=4×2=8.
解决这类与菱形相关的几何问题时,往往需要先根据题中给出的已知条件选择合适的判定方法证明四边形为菱形,最后再结合菱形的性质求解.
方法归纳总结:
典型例题
【当堂检测】
4.一个平行四边形的一条边长是9,两条对角线的长分别是12和 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
是特殊的平行四边形,
A
B
C
D
O
理由:如右图, ABCD中,AC= ,BD=12,AD=9,
∵平行四边形对角线互相平分,
∴OA=0C= ,OD=OB=6,
∵62 + =92,
∴△AOD是直角三角形,AO⊥DO,
∴AC⊥BD,
∴四边形ABCD是菱形,是特殊的平行四边形
S菱形ABCD= BD·AC= ×12× =
四、课堂总结
2.菱形的判定定理:
对角线互相垂直的平行四边形是菱形;
四条边相等的四边形是菱形.
1.菱形的定义:
有一组邻边相等的平行四边形是菱形.
第十八章 平行四边形
18.2.2 菱形
第2课时
1.能利用菱形的定义来判定一个四边形为菱形
2.能探究菱形的判定定理,会判定一个四边形为菱形
3.能解决与菱形相关的简单几何问题
一、学习目标
二、新课导入
那么怎样判断一个四边形是否是菱形呢
生活中很多服装设计者在设计服装的时候,往往青睐于菱形图案的设计.这是因为菱形的特殊因素能给人一种舒服的感觉.
三、概念剖析
由菱形的定义可知,有一组邻边相等的平行四边形是菱形.除此之外,还有没有其他判定方法呢?
思考:我们知道,菱形的对角线互相垂直.反过来,对角线互相垂直的平行四边形是菱形吗?
三、概念剖析
证明:∵四边形ABCD是平行四边形,
∴OA=OC
又∵AC⊥BD,
∴BD是线段AC的垂直平分线
∴BA=BC
∴四边形ABCD是菱形(菱形的定义)
菱形的判定定理1:
对角线互相垂直的平行四边形是菱形.
证一证:已知:如图,在□ABCD中,对角线AC与BD交于点O,AC⊥BD.
求证: □ABCD是菱形
典型例题
例1.如图,在 ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.求证:四边形AFBE是菱形.
分析:由平行四边形的性质得出AD∥BC,得出∠AEG=∠BFG,由AAS证明△AGE≌△BGF,得出AE=BF,由AD∥BC,可证四边形AFBE是平行四边形,由EF⊥AB,即可得出结论.
典型例题
例1.如图,在 ABCD中,边AB的垂直平分线交AD于点E,交CB的延长线于点F,连接AF、BE.求证:四边形AFBE是菱形.
证明:∵四边形ABCD是平行四边形,
∴AD∥BC,即AD∥FC
∴∠AEG=∠BFG,
∵EF垂直平分AB,
∴AG=BG,且∠AEG=∠BFG,∠AGE=∠BGF
∴△AGE≌△BGF(AAS);
∴AE=BF,
∵AD∥FC,
∴四边形AFBE是平行四边形,
又∵EF⊥AB,
∴四边形AFBE是菱形.(对角线互相垂直的平行四边形是菱形)
1.如图,平行四边形ABCD的两条对角线AC、BD相交于点O,AB=5,AO=4,BO=3.求证:四边形ABCD是菱形.
【当堂检测】
A
B
C
D
O
证明:∵OA=4,OB=3,AB=5,
∴ AB =OA +OB ,
∴△AOB是直角三角形,即AC⊥BD,
∴四边形ABCD是菱形.
三、概念剖析
思考:前面的研究中我们知道菱形的四条边相等,反过来,四条边相等的四边形是菱形吗?
证一证:已知:如图,四边形ABCD中,AB=BC=CD=DA.
求证:四边形ABCD是菱形
证明:∵AB=CD,AD=BC
∴四边形ABCD是平行四边形
又∵AB=BC
∴四边形ABCD是菱形(菱形的定义)
菱形的判定定理2:
四条边相等的四边形是菱形.
例2.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
典型例题
分析:根据平移的性质可得CF=AD,DF=AC,再在Rt△ABC中利用勾股定理求出AC的长,最后根据四条边都相等的四边形是菱形得到结论.
例2.如图所示,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
典型例题
证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.(四条边相等的四边形是菱形)
∴AC=
【当堂检测】
2.如图,△ABC是等腰三角形,把它沿底边BC翻折后,得到△DBC,则四边形ABDC为 ,理由是 .
菱形
四条边相等的四边形是菱形
【当堂检测】
3.如图,在△ABC中,点D,E,F分别是AB,AC,BC的中点,AF⊥BC.
求证:四边形ADFE是菱形.
证明:∵AF⊥BC,点D,E,F分别是AB,AC,BC的中点,
∴DF=AD=EF=AE,
∴四边形ADFE是菱形.
∴AB=AC,DF= AC=AE,EF= AB=AD,
典型例题
例3.如图,在 ABCD中,AC平分∠DAB,AB=2,求 ABCD的周长.
点拨:求 ABCD的周长可先证明 ABCD是菱形.
解:∵四边形ABCD为平行四边形,
∴∠DAC=∠ACB,
又∵AC平分∠DAB,
∴∠DAC=∠BAC,
∴∠ACB=∠BAC,
∴平行四边形ABCD为菱形,(有一组邻边相等的平行四边形是菱形)
又∵AB=2,
∴AD∥BC,
∴AB=BC,
∴四边形ABCD的周长=4×2=8.
解决这类与菱形相关的几何问题时,往往需要先根据题中给出的已知条件选择合适的判定方法证明四边形为菱形,最后再结合菱形的性质求解.
方法归纳总结:
典型例题
【当堂检测】
4.一个平行四边形的一条边长是9,两条对角线的长分别是12和 ,这是一个特殊的平行四边形吗?为什么?求出它的面积.
是特殊的平行四边形,
A
B
C
D
O
理由:如右图, ABCD中,AC= ,BD=12,AD=9,
∵平行四边形对角线互相平分,
∴OA=0C= ,OD=OB=6,
∵62 + =92,
∴△AOD是直角三角形,AO⊥DO,
∴AC⊥BD,
∴四边形ABCD是菱形,是特殊的平行四边形
S菱形ABCD= BD·AC= ×12× =
四、课堂总结
2.菱形的判定定理:
对角线互相垂直的平行四边形是菱形;
四条边相等的四边形是菱形.
1.菱形的定义:
有一组邻边相等的平行四边形是菱形.
