18.2.2 菱形 第1课时 课件(共15张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 18.2.2 菱形 第1课时 课件(共15张PPT) 2023-2024学年初中数学人教版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 11:27:27 | ||
图片预览



文档简介
(共15张PPT)
第十八章 平行四边形
18.2.2 菱形
第1课时
1.能理解菱形的定义,知道菱形是特殊的平行四边形
2.能理解菱形具有平行四边形的所有性质,探究菱形的特殊性质
3.能根据对角线计算菱形的边长、周长、面积.
一、学习目标
二、新课导入
复习回顾
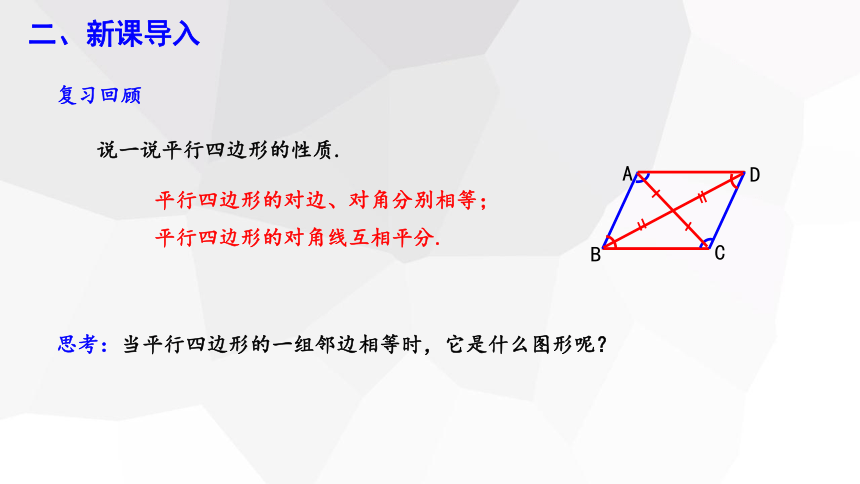
说一说平行四边形的性质.
平行四边形的对边、对角分别相等;
平行四边形的对角线互相平分.
思考:当平行四边形的一组邻边相等时,它是什么图形呢?
A
B
D
C
三、概念剖析
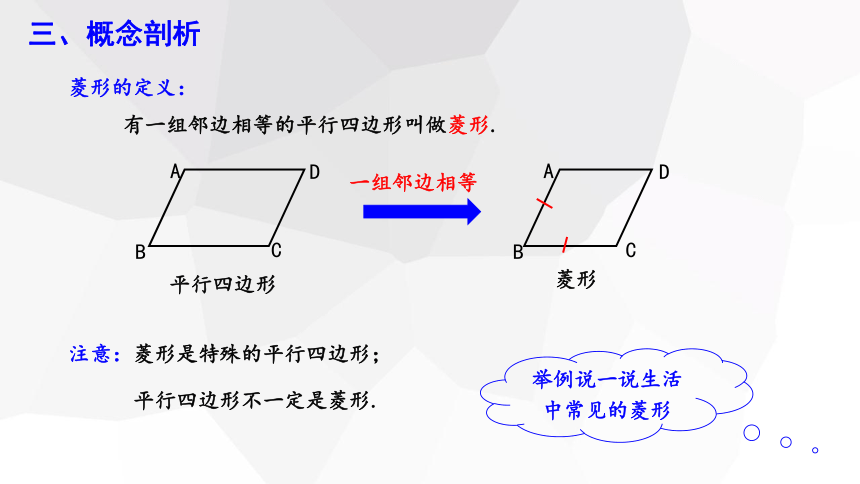
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
A
B
D
C
一组邻边相等
平行四边形
菱形
注意:菱形是特殊的平行四边形;
举例说一说生活中常见的菱形
A
B
D
C
平行四边形不一定是菱形.
三、概念剖析
菱形的性质:(除具有平行四边形的性质外)
性质1:菱形的四条边都相等;
证一证:如图,在菱形ABCD中,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
性质2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
A
B
C
O
D
证明:∵四边形ABCD是菱形,
∴AB=AD,AB=BC,BC=CD,CD=AD (有一组邻边相等)
∴AB = BC = CD =AD.
三、概念剖析
A
B
C
O
D
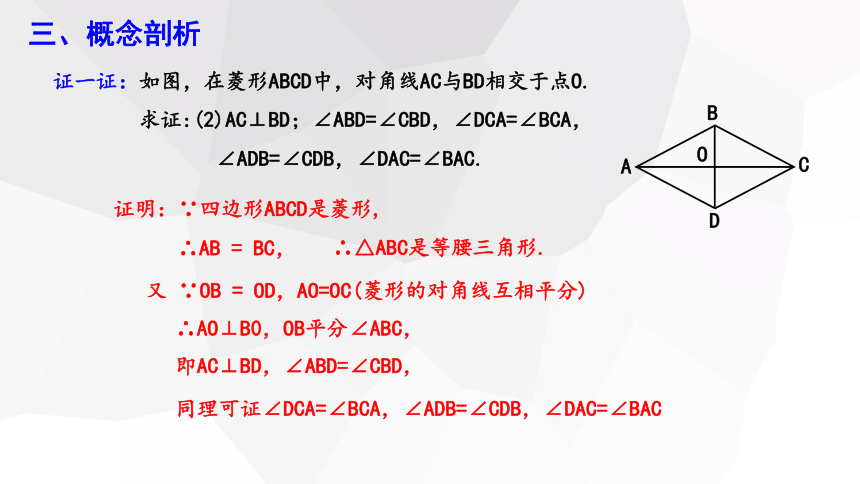
证一证:如图,在菱形ABCD中,对角线AC与BD相交于点O.
求证:(2)AC⊥BD;∠ABD=∠CBD,∠DCA=∠BCA,
∠ADB=∠CDB,∠DAC=∠BAC.
证明:∵四边形ABCD是菱形,
∴△ABC是等腰三角形.
∴AB = BC,
又 ∵OB = OD,AO=OC(菱形的对角线互相平分)
∴AO⊥B0,OB平分∠ABC,
即AC⊥BD,∠ABD=∠CBD,
同理可证∠DCA=∠BCA,∠ADB=∠CDB,∠DAC=∠BAC
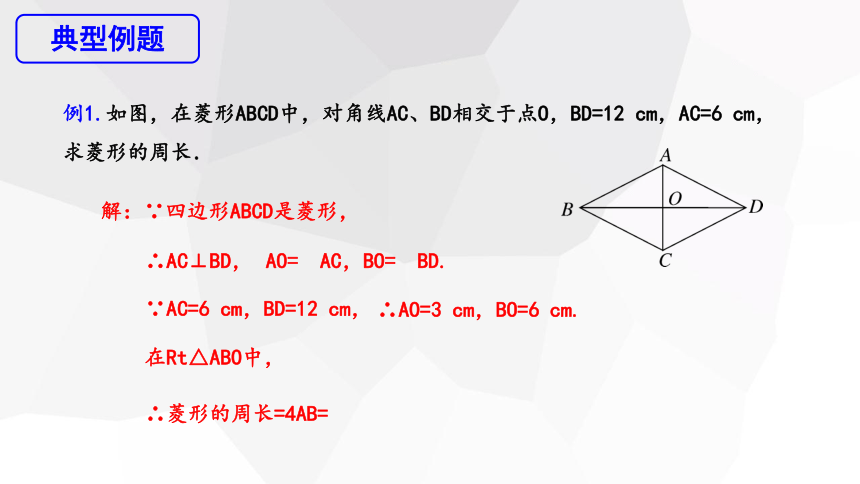
例1.如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12 cm,AC=6 cm,求菱形的周长.
典型例题
解:∵四边形ABCD是菱形,
AO= AC,BO= BD.
在Rt△ABO中,
∴菱形的周长=4AB=
∴AC⊥BD,
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
小结:
(1)菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
(2)菱形的周长=边长的4倍.
典型例题
1.如图,菱形ABCD的周长为48 cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
6 cm
【当堂检测】
三、概念剖析
菱形的面积:
观察下图,菱形的对角线把菱形分成四个全等的直角三角形.
A
B
C
D
O
即 △AOB≌△AOD≌△COD≌△COB
得到菱形的面积公式:
S菱形ABCD=4S△AOB=
自己动手证一证
4× ×OA×OB
= AC·BD
即 菱形的面积可以等于 乘以两条对角线的积.
例2.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果分别精确到0.01m和0.1m2 ).
典型例题
A
B
C
D
O
解:∵花坛ABCD是菱形,
2.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为 .
30
【当堂检测】
例3.如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.(AAS)
∴AE=AF.
归纳:菱形是轴对称图形,它的对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
典型例题
3.如图,菱形ABCD中,O是对角线AC上一点,连接OB,OD,求证:OB=OD.
【当堂检测】
证明:∵四边形ABCD是菱形,
∴AB=AD,∠CAB=∠CAD,
在△ABO和△ADO中
∴△ABO≌△ADO,(SAS)
∴OB=OD;
四、课堂总结
1.菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
2.菱形的性质:(除具有平行四边形的性质外)
3.菱形的面积公式:
A
B
C
O
D
性质1:菱形的四条边都相等;
性质2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形的面积可以等于 乘以两条对角线的积.
第十八章 平行四边形
18.2.2 菱形
第1课时
1.能理解菱形的定义,知道菱形是特殊的平行四边形
2.能理解菱形具有平行四边形的所有性质,探究菱形的特殊性质
3.能根据对角线计算菱形的边长、周长、面积.
一、学习目标
二、新课导入
复习回顾
说一说平行四边形的性质.
平行四边形的对边、对角分别相等;
平行四边形的对角线互相平分.
思考:当平行四边形的一组邻边相等时,它是什么图形呢?
A
B
D
C
三、概念剖析
菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
A
B
D
C
一组邻边相等
平行四边形
菱形
注意:菱形是特殊的平行四边形;
举例说一说生活中常见的菱形
A
B
D
C
平行四边形不一定是菱形.
三、概念剖析
菱形的性质:(除具有平行四边形的性质外)
性质1:菱形的四条边都相等;
证一证:如图,在菱形ABCD中,对角线AC与BD相交于点O.
求证:(1)AB = BC = CD =AD;
性质2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
A
B
C
O
D
证明:∵四边形ABCD是菱形,
∴AB=AD,AB=BC,BC=CD,CD=AD (有一组邻边相等)
∴AB = BC = CD =AD.
三、概念剖析
A
B
C
O
D
证一证:如图,在菱形ABCD中,对角线AC与BD相交于点O.
求证:(2)AC⊥BD;∠ABD=∠CBD,∠DCA=∠BCA,
∠ADB=∠CDB,∠DAC=∠BAC.
证明:∵四边形ABCD是菱形,
∴△ABC是等腰三角形.
∴AB = BC,
又 ∵OB = OD,AO=OC(菱形的对角线互相平分)
∴AO⊥B0,OB平分∠ABC,
即AC⊥BD,∠ABD=∠CBD,
同理可证∠DCA=∠BCA,∠ADB=∠CDB,∠DAC=∠BAC
例1.如图,在菱形ABCD中,对角线AC、BD相交于点O,BD=12 cm,AC=6 cm,求菱形的周长.
典型例题
解:∵四边形ABCD是菱形,
AO= AC,BO= BD.
在Rt△ABO中,
∴菱形的周长=4AB=
∴AC⊥BD,
∵AC=6 cm,BD=12 cm,
∴AO=3 cm,BO=6 cm.
小结:
(1)菱形是特殊的平行四边形,它除具有平行四边形的所有性质外,还有平行四边形所没有的特殊性质.
(2)菱形的周长=边长的4倍.
典型例题
1.如图,菱形ABCD的周长为48 cm,对角线AC、BD相交于O点,E是AD的中点,连接OE,则线段OE的长为_______.
6 cm
【当堂检测】
三、概念剖析
菱形的面积:
观察下图,菱形的对角线把菱形分成四个全等的直角三角形.
A
B
C
D
O
即 △AOB≌△AOD≌△COD≌△COB
得到菱形的面积公式:
S菱形ABCD=4S△AOB=
自己动手证一证
4× ×OA×OB
= AC·BD
即 菱形的面积可以等于 乘以两条对角线的积.
例2.如图,菱形花坛ABCD的边长为20m,∠ABC=60°,沿着菱形的对角线修建了两条小路AC和BD,求两条小路的长和花坛的面积(结果分别精确到0.01m和0.1m2 ).
典型例题
A
B
C
D
O
解:∵花坛ABCD是菱形,
2.如图,在菱形ABCD中,对角线AC=6,BD=10,则菱形ABCD的面积为 .
30
【当堂检测】
例3.如图,在菱形ABCD中,CE⊥AB于点E,CF⊥AD于点F,求证:AE=AF.
证明:连接AC.
∵四边形ABCD是菱形,
∴AC平分∠BAD,即∠BAC=∠DAC.
∵CE⊥AB,CF⊥AD,
∴∠AEC=∠AFC=90°.
又∵AC=AC,
∴△ACE≌△ACF.(AAS)
∴AE=AF.
归纳:菱形是轴对称图形,它的对角线所在的直线都是它的对称轴,每条对角线平分一组对角.
典型例题
3.如图,菱形ABCD中,O是对角线AC上一点,连接OB,OD,求证:OB=OD.
【当堂检测】
证明:∵四边形ABCD是菱形,
∴AB=AD,∠CAB=∠CAD,
在△ABO和△ADO中
∴△ABO≌△ADO,(SAS)
∴OB=OD;
四、课堂总结
1.菱形的定义:
有一组邻边相等的平行四边形叫做菱形.
2.菱形的性质:(除具有平行四边形的性质外)
3.菱形的面积公式:
A
B
C
O
D
性质1:菱形的四条边都相等;
性质2:菱形的两条对角线互相垂直,并且每一条对角线平分一组对角.
菱形的面积可以等于 乘以两条对角线的积.
