18.2.3 正方形 课件(共19张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 18.2.3 正方形 课件(共19张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 514.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 00:00:00 | ||
图片预览





文档简介
(共19张PPT)
第十八章 平行四边形
18.2.3 正方形
1.能从边、内角、对角线三个方面掌握正方形的所有性质
2.能掌握正方形不同的判定方法,能根据已知条件选择正确的方法判定正方形
3.能理解正方形、菱形、矩形、平行四边形之间的关系
4.能解决与正方形相关的几何问题
一、学习目标
二、新课导入
观察图片中框出的图形,正方形是我们熟悉的几何图形,在生活中无处不在.
思考:正方形都有些什么特点呢?
三、概念剖析
正方形是特殊的平行四边形,它的四条边都相等,四个角都是直角.因此,正方形既是矩形,又是菱形.它既有矩形的性质,又有菱形的性质.
(一)正方形的性质
(1)边:
正方形的对边相等且平行,四条边都相等;
(2)内角:
对角相等,且四个角都相等,都为直角;
(3)对角线:
对角线相等且互相垂直平分.
A
B
C
D
三、概念剖析
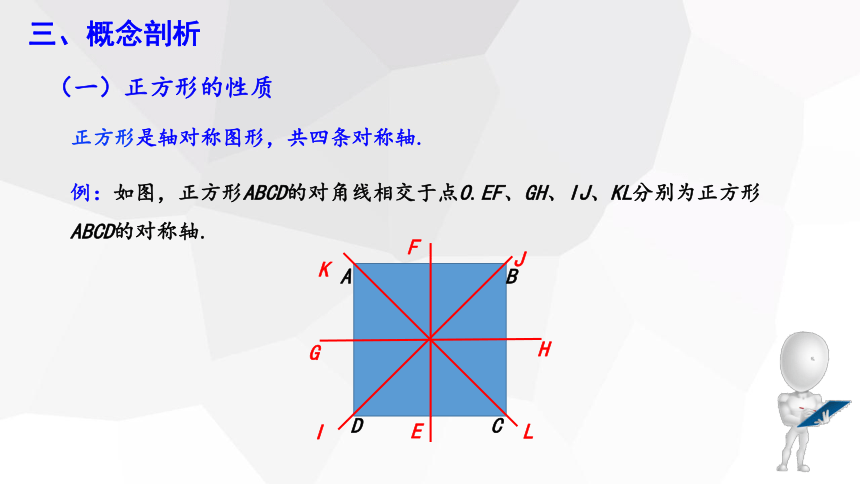
正方形是轴对称图形,共四条对称轴.
例:如图,正方形ABCD的对角线相交于点O.EF、GH、IJ、KL分别为正方形ABCD的对称轴.
F
E
H
G
I
J
K
L
(一)正方形的性质
三、概念剖析
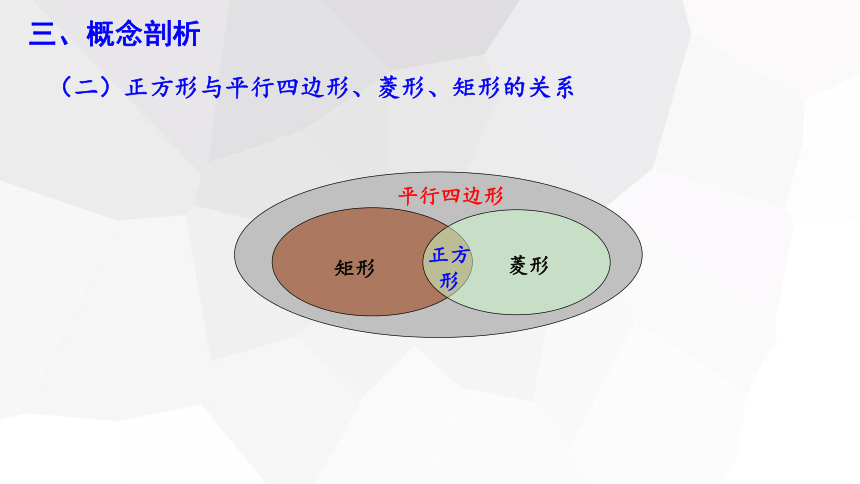
(二)正方形与平行四边形、菱形、矩形的关系
平行四边形
矩形
菱形
正方形
典型例题
例1.已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是
等腰直角三角形
∴△ABO≌ △BCO ≌ △CDO ≌ △DAO.
又∵ AD=CD=BC=AB
归纳:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
典型例题
例2.如图,在正方形ABCD中,ΔBEC是等边三角形,求证:∠EAD=∠EDA=15°.
点拨:由正方形ABCD和△BEC是等边三角形可得△ABE和△DCE是等腰三角形,得到∠BAE和∠CDE的度数,从而证明即可.
典型例题
证明:∵ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵四边形ABCD是正方形,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
例2.如图,在正方形ABCD中,ΔBEC是等边三角形,求证:∠EAD=∠EDA=15°.
1.正方形具有而菱形不一定具有的性质( )
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
D
【当堂检测】
在Rt△AOD中,由勾股定理,得
2.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
∴正方形的周长为4AD= ,面积为AD2=8.
【当堂检测】
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2,
三、概念剖析
正方形既是矩形,又是菱形.即,
(1)有一组邻边相等的矩形是正方形.(或对角线互相垂直的矩形是正方形)
(三)正方形的判定
矩 形
邻边相等
正方形
对角线互相垂直
三、概念剖析
(三)正方形的判定
(2)有一个角是直角的菱形是正方形.(或对角线相等的矩形是正方形)
菱 形
一个角是直角
正方形
对角线相等
例2.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
典型例题
点拨:由题意得,四边形CFDE是矩形,根据角平分线的性质可得DE=DF,据此判定四边形CFDE是正方形.
证明:∵∠C=90°,DE⊥BC于E,DF⊥AC于F,
∴四边形CFDE是矩形,
又∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,
∴四边形CFDE是正方形.(有一组邻边相等的矩形是正方形)
例3.如图所示,已知□ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.若∠AED=2∠EAD.求证:四边形ABCD是正方形.
典型例题
证明:∵四边形ABCD是平行四边形,
∴AO=CO.
又∵△ACE是等边三角形,
∴EO⊥AC,即DB⊥AC.
∴平行四边形ABCD是菱形.
∵△ACE是等边三角形,
∴∠AEC=60°.
∵∠AED=2∠EAD,
∴∠EAD=15°.
∴∠ADO=∠EAD+∠AED=45°.
∵四边形ABCD是菱形,
∴∠ADC=2∠ADO=90°.
∴菱形ABCD是正方形.(有一个角是直角的菱形是正方形)
∴∠AEO= ∠AEC=30°.
总结:
正方形判定的两条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件
菱形条件
(1)
(2)
一个直角
对角线相等
一组邻边相等
对角线垂直
典型例题
3.平行四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:
使得平行四边形ABCD是正方形.
【当堂检测】
∠BAD=90°或AC=BD
4.已知:如图所示,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.
证明:过点D作DG⊥AB于点G.
∵DF⊥AC,DE⊥BC,
∴∠DFC=∠DEC=90°.
又∵∠C=90°,
∴四边形CEDF是矩形
∵AD平分∠BAC,DF⊥AC,DG⊥AB,
∴DF=DG.
同理可得DE=DG,∴DE=DF.
∴四边形CEDF是正方形.
G
∴∠DAF=∠DAG,∠AFD=∠AGD=90°
又∵AD=AD
∴△AFD≌△ADG(AAS),
【当堂检测】
四、课堂总结
1.正方形的性质:
(1)边:
正方形的对边相等且平行,四条边都相等;
(2)内角:
对角相等,且四个角都相等,都为直角;
(3)对角线:
对角线相等且互相垂直平分.
2.正方形的判定:
(1)有一组邻边相等的矩形是正方形.(或对角线互相垂直的矩形是正方形)
(2)有一个角是直角的菱形是正方形.(或对角线相等的矩形是正方形)
第十八章 平行四边形
18.2.3 正方形
1.能从边、内角、对角线三个方面掌握正方形的所有性质
2.能掌握正方形不同的判定方法,能根据已知条件选择正确的方法判定正方形
3.能理解正方形、菱形、矩形、平行四边形之间的关系
4.能解决与正方形相关的几何问题
一、学习目标
二、新课导入
观察图片中框出的图形,正方形是我们熟悉的几何图形,在生活中无处不在.
思考:正方形都有些什么特点呢?
三、概念剖析
正方形是特殊的平行四边形,它的四条边都相等,四个角都是直角.因此,正方形既是矩形,又是菱形.它既有矩形的性质,又有菱形的性质.
(一)正方形的性质
(1)边:
正方形的对边相等且平行,四条边都相等;
(2)内角:
对角相等,且四个角都相等,都为直角;
(3)对角线:
对角线相等且互相垂直平分.
A
B
C
D
三、概念剖析
正方形是轴对称图形,共四条对称轴.
例:如图,正方形ABCD的对角线相交于点O.EF、GH、IJ、KL分别为正方形ABCD的对称轴.
F
E
H
G
I
J
K
L
(一)正方形的性质
三、概念剖析
(二)正方形与平行四边形、菱形、矩形的关系
平行四边形
矩形
菱形
正方形
典型例题
例1.已知: 如图,四边形ABCD是正方形,对角线AC、BD相交于点O.
求证: △ABO、 △BCO、 △CDO、 △DAO是全等的等腰直角三角形.
A
D
C
B
O
证明: ∵ 四边形ABCD是正方形,
∴ AC=BD,AC⊥BD,AO=BO=CO=DO.
∴ △ABO、 △BCO、 △CDO、 △DAO都是
等腰直角三角形
∴△ABO≌ △BCO ≌ △CDO ≌ △DAO.
又∵ AD=CD=BC=AB
归纳:正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.
典型例题
例2.如图,在正方形ABCD中,ΔBEC是等边三角形,求证:∠EAD=∠EDA=15°.
点拨:由正方形ABCD和△BEC是等边三角形可得△ABE和△DCE是等腰三角形,得到∠BAE和∠CDE的度数,从而证明即可.
典型例题
证明:∵ΔBEC是等边三角形,
∴BE=CE=BC,∠EBC=∠ECB=60°,
∵四边形ABCD是正方形,
∴AB=BE=CE=CD,∠ABE=∠DCE=30°,
∴AB=BC=CD,∠ABC=∠DCB=90°,
∴△ABE,△DCE是等腰三角形,
∴∠BAE=∠BEA=∠CDE=∠CED=75°,
∴∠EAD=∠EDA=90°-75°=15°.
例2.如图,在正方形ABCD中,ΔBEC是等边三角形,求证:∠EAD=∠EDA=15°.
1.正方形具有而菱形不一定具有的性质( )
A.四条边相等 B.对角线互相垂直平分
C.对角线平分一组对角 D.对角线相等
D
【当堂检测】
在Rt△AOD中,由勾股定理,得
2.如图,四边形ABCD是正方形,对角线AC与BD相交于点O,AO=2,求正方形的周长与面积.
∴正方形的周长为4AD= ,面积为AD2=8.
【当堂检测】
解:∵四边形ABCD是正方形,
∴AC⊥BD,OA=OD=2,
三、概念剖析
正方形既是矩形,又是菱形.即,
(1)有一组邻边相等的矩形是正方形.(或对角线互相垂直的矩形是正方形)
(三)正方形的判定
矩 形
邻边相等
正方形
对角线互相垂直
三、概念剖析
(三)正方形的判定
(2)有一个角是直角的菱形是正方形.(或对角线相等的矩形是正方形)
菱 形
一个角是直角
正方形
对角线相等
例2.已知:如图,△ABC中,∠C=90°,CD平分∠ACB,DE⊥BC于E,DF⊥AC于F.求证:四边形CFDE是正方形.
典型例题
点拨:由题意得,四边形CFDE是矩形,根据角平分线的性质可得DE=DF,据此判定四边形CFDE是正方形.
证明:∵∠C=90°,DE⊥BC于E,DF⊥AC于F,
∴四边形CFDE是矩形,
又∵CD平分∠ACB,DE⊥BC,DF⊥AC,
∴DE=DF,
∴四边形CFDE是正方形.(有一组邻边相等的矩形是正方形)
例3.如图所示,已知□ABCD中,对角线AC,BD交于点O,E是BD延长线上的点,且△ACE是等边三角形.若∠AED=2∠EAD.求证:四边形ABCD是正方形.
典型例题
证明:∵四边形ABCD是平行四边形,
∴AO=CO.
又∵△ACE是等边三角形,
∴EO⊥AC,即DB⊥AC.
∴平行四边形ABCD是菱形.
∵△ACE是等边三角形,
∴∠AEC=60°.
∵∠AED=2∠EAD,
∴∠EAD=15°.
∴∠ADO=∠EAD+∠AED=45°.
∵四边形ABCD是菱形,
∴∠ADC=2∠ADO=90°.
∴菱形ABCD是正方形.(有一个角是直角的菱形是正方形)
∴∠AEO= ∠AEC=30°.
总结:
正方形判定的两条途径:
正方形
正方形
+
+
先判定菱形
先判定矩形
矩形条件
菱形条件
(1)
(2)
一个直角
对角线相等
一组邻边相等
对角线垂直
典型例题
3.平行四边形ABCD的对角线AC与BD相交于点O,且AC⊥BD,请添加一个条件:
使得平行四边形ABCD是正方形.
【当堂检测】
∠BAD=90°或AC=BD
4.已知:如图所示,在Rt△ABC中,∠C=90°,∠BAC,∠ABC的平分线交于点D,DE⊥BC于点E,DF⊥AC于点F.求证:四边形CEDF是正方形.
证明:过点D作DG⊥AB于点G.
∵DF⊥AC,DE⊥BC,
∴∠DFC=∠DEC=90°.
又∵∠C=90°,
∴四边形CEDF是矩形
∵AD平分∠BAC,DF⊥AC,DG⊥AB,
∴DF=DG.
同理可得DE=DG,∴DE=DF.
∴四边形CEDF是正方形.
G
∴∠DAF=∠DAG,∠AFD=∠AGD=90°
又∵AD=AD
∴△AFD≌△ADG(AAS),
【当堂检测】
四、课堂总结
1.正方形的性质:
(1)边:
正方形的对边相等且平行,四条边都相等;
(2)内角:
对角相等,且四个角都相等,都为直角;
(3)对角线:
对角线相等且互相垂直平分.
2.正方形的判定:
(1)有一组邻边相等的矩形是正方形.(或对角线互相垂直的矩形是正方形)
(2)有一个角是直角的菱形是正方形.(或对角线相等的矩形是正方形)
