19.1.1 变量与函数 第1课时 课件(共14张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.1.1 变量与函数 第1课时 课件(共14张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 263.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 11:28:17 | ||
图片预览






文档简介
(共14张PPT)
第十九章 一次函数
19.1.1 变量与函数
第1课时
1.掌握变量与常量的概念,能区分实际问题中的变量与常量
2.知道在特定的问题情境中,其中一个变量的值会随着另一个变量的值的变化而变化
一、学习目标
二、新课导入
观察下图你能发现什么?
世间万物随着时间变化而变化
例1.汽车以60 km/h的速度匀速行驶,行驶路程为s km,行驶时间为t h,
(1)上述的哪些量在发生变化?哪些量不变呢?
行驶路程s km、行驶时间t h是变化的;
行驶速度60 km/h是不变的.
二、典型例题
例1.汽车以60 km/h的速度匀速行驶,行驶路程为s km,行驶时间为t h,
(2)试补充完下表:
t/h 1 2 3 4 5 t
s/km
60
120
180
240
300
60t
(3)s的值随t的值的变化而变化吗?
路程s的值随时间t的值的变化而变化
二、典型例题
得出定义:
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
例:s、t为变量,60为常量.
二、典型例题
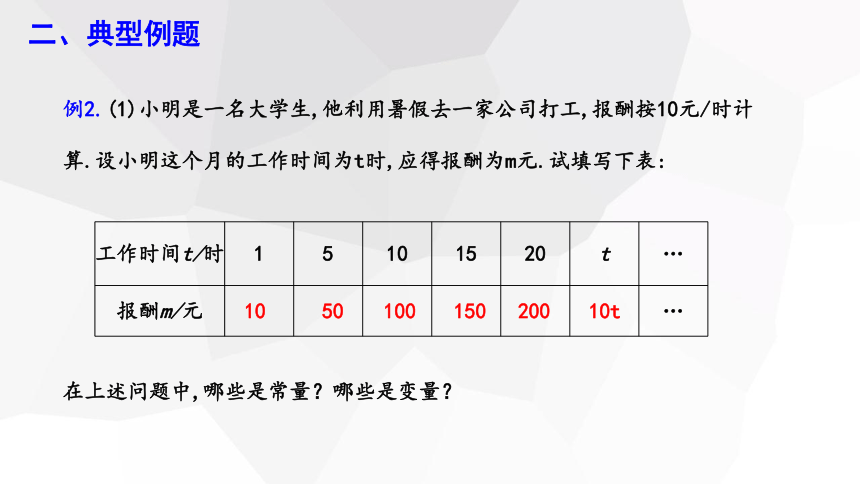
例2.(1)小明是一名大学生,他利用暑假去一家公司打工,报酬按10元/时计算.设小明这个月的工作时间为t时,应得报酬为m元.试填写下表:
工作时间t/时 1 5 10 15 20 t …
报酬m/元 …
10
50
100
150
200
10t
二、典型例题
在上述问题中,哪些是常量?哪些是变量?
分析:题中不变的量是工作一小时10元的报酬,变化的量是这个月的工作时间t时和应得报酬m元,再依据常量和变量的定义即可答题.
变量:工作时间t、应得报酬m;
常量:工作一小时10元的报酬.
二、典型例题
二、典型例题
例2.(2)指出其中的常量与变量:运动员在400 m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步速度v(m/s)之间的关系为 .
分析:题中不变的量是400 m一圈的跑道,变化的量是跑一圈所用的时间t和跑步速度v,再依据常量和变量的定义即可答题.
变量:跑一圈所用的时间t和跑步速度v;
常量:400 m一圈的跑道.
方法总结:
在实际生活中,一些问题情境通常涉及几个量,其中已知(或数值不变)的量是常量,未知(或数值变化)的量是变量.理解问题情境中各个量之间的关系,需要我们具备一定的生活常识.
二、典型例题
【当堂检测】
1.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量
C.单价 D.金额和数量
C
【当堂检测】
2.(1)圆的半径为r,圆的面积S与半径r之间有如下关系:S=πr2.在这关系中,常量是 ,变量是 .
(2)每张电影票的售价为10元,某日共售出x张票,票房收入为y元,在这一问题中, 是常量, 是变量.
π
S、r
电影票的售价
电影票的张数,票房收入
【当堂检测】
变量是x、y,常量是4.
3.指出下列问题中的变量和常量:
某市的自来水价为4元/t,现要抽取若干户居民调查水费支出情况,记某户月用水量为x t,月应交水费为y元.
四、课堂总结
常量与变量:
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
第十九章 一次函数
19.1.1 变量与函数
第1课时
1.掌握变量与常量的概念,能区分实际问题中的变量与常量
2.知道在特定的问题情境中,其中一个变量的值会随着另一个变量的值的变化而变化
一、学习目标
二、新课导入
观察下图你能发现什么?
世间万物随着时间变化而变化
例1.汽车以60 km/h的速度匀速行驶,行驶路程为s km,行驶时间为t h,
(1)上述的哪些量在发生变化?哪些量不变呢?
行驶路程s km、行驶时间t h是变化的;
行驶速度60 km/h是不变的.
二、典型例题
例1.汽车以60 km/h的速度匀速行驶,行驶路程为s km,行驶时间为t h,
(2)试补充完下表:
t/h 1 2 3 4 5 t
s/km
60
120
180
240
300
60t
(3)s的值随t的值的变化而变化吗?
路程s的值随时间t的值的变化而变化
二、典型例题
得出定义:
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
例:s、t为变量,60为常量.
二、典型例题
例2.(1)小明是一名大学生,他利用暑假去一家公司打工,报酬按10元/时计算.设小明这个月的工作时间为t时,应得报酬为m元.试填写下表:
工作时间t/时 1 5 10 15 20 t …
报酬m/元 …
10
50
100
150
200
10t
二、典型例题
在上述问题中,哪些是常量?哪些是变量?
分析:题中不变的量是工作一小时10元的报酬,变化的量是这个月的工作时间t时和应得报酬m元,再依据常量和变量的定义即可答题.
变量:工作时间t、应得报酬m;
常量:工作一小时10元的报酬.
二、典型例题
二、典型例题
例2.(2)指出其中的常量与变量:运动员在400 m一圈的跑道上训练,他跑一圈所用的时间t(s)与跑步速度v(m/s)之间的关系为 .
分析:题中不变的量是400 m一圈的跑道,变化的量是跑一圈所用的时间t和跑步速度v,再依据常量和变量的定义即可答题.
变量:跑一圈所用的时间t和跑步速度v;
常量:400 m一圈的跑道.
方法总结:
在实际生活中,一些问题情境通常涉及几个量,其中已知(或数值不变)的量是常量,未知(或数值变化)的量是变量.理解问题情境中各个量之间的关系,需要我们具备一定的生活常识.
二、典型例题
【当堂检测】
1.李师傅到单位附近的加油站加油,如图是所用的加油机上的数据显示牌,则其中的常量是( )
A.金额 B.数量
C.单价 D.金额和数量
C
【当堂检测】
2.(1)圆的半径为r,圆的面积S与半径r之间有如下关系:S=πr2.在这关系中,常量是 ,变量是 .
(2)每张电影票的售价为10元,某日共售出x张票,票房收入为y元,在这一问题中, 是常量, 是变量.
π
S、r
电影票的售价
电影票的张数,票房收入
【当堂检测】
变量是x、y,常量是4.
3.指出下列问题中的变量和常量:
某市的自来水价为4元/t,现要抽取若干户居民调查水费支出情况,记某户月用水量为x t,月应交水费为y元.
四、课堂总结
常量与变量:
在一个变化过程中,我们称数值发生变化的量为变量,数值始终不变的量为常量.
