19.1.1 变量与函数 第2课时 课件(共17张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.1.1 变量与函数 第2课时 课件(共17张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 248.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 10:52:10 | ||
图片预览





文档简介
(共17张PPT)
第十九章 一次函数
19.1.1 变量与函数
第2课时
1.了解函数的相关概念,会判断两个变量是否具有函数关系.
2.能根据简单的实际问题写出函数解析式,并确定自变量的取值范围.
3.会根据函数解析式求函数值.
一、学习目标
二、新课导入
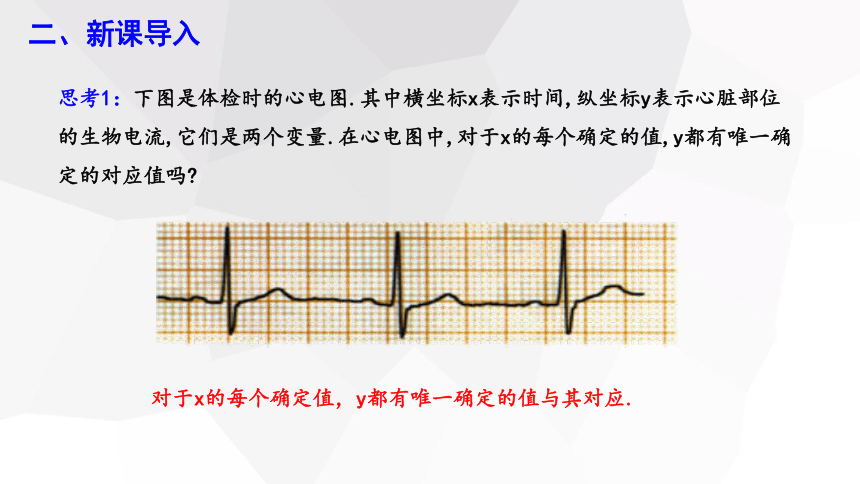
思考1:下图是体检时的心电图.其中横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每个确定的值,y都有唯一确定的对应值吗
对于x的每个确定值,y都有唯一确定的值与其对应.
二、新课导入
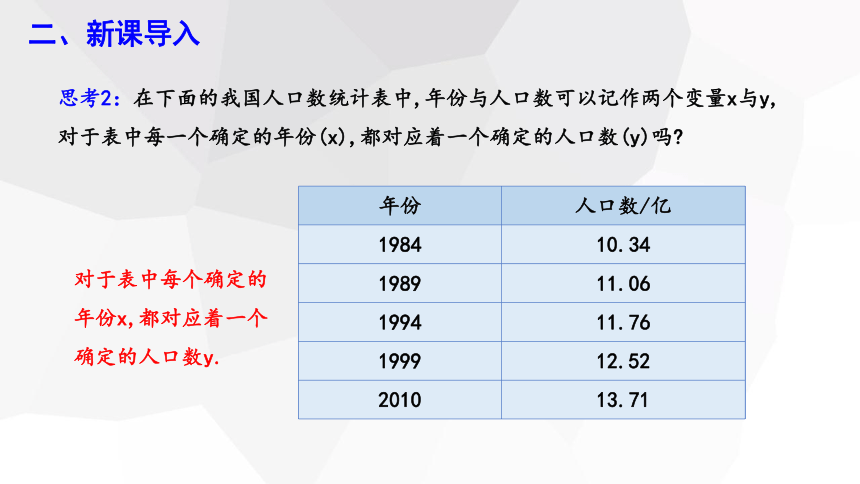
思考2:在下面的我国人口数统计表中,年份与人口数可以记作两个变量x与y,对于表中每一个确定的年份(x),都对应着一个确定的人口数(y)吗
年份
人口数/亿
1984
10.34
1989
11.06
1994
11.76
1999
12.52
2010
13.71
对于表中每个确定的年份x,都对应着一个确定的人口数y.
三、概念剖析
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
(一)函数
例:前面的思考,在心电图中,时间x是自变量,心脏部位的生物电流y是x的函数;
在人口统计表中,年份x是自变量,人口数y是x的函数.
三、概念剖析
(二)函数值
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
例:在人口统计表中,当x=2010时,函数值y=13.71.
四、典型例题
例1.观察并判断下列式子中的y是x的函数吗?为什么?
(1)y=3x﹣5; (2)y= ; (3)x﹣y2=0;
解:(1)y是x的函数,
y=3x﹣5满足对于x的每一个取值,y都有唯一确定的值与之对应关系;
(2)y是x的函数,
满足对于x的每一个取值,y都有唯一确定的值与之对应关系;
(3)y不是x的函数,
x﹣y2=0即y2=x,当x=4时,y=2或﹣2,不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,y不是x的函数.
四、典型例题
(4)y= ; (5)|y|=x.
(4)y是x的函数,
满足对于x的每一个取值,y都有唯一确定的值与之对应关系;
(5)y不是x的函数,
当x=4时,y=4或﹣4,不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,y不是x的函数.
【当堂检测】
1.下列式子中,y不是x的函数的是( )
A.y=-x+3 B. C. D.y=-x
B
【当堂检测】
2.在下列关系式中:①长方形的宽一定时,其长与面积的关系;②等腰三角形的底边长与面积;③圆的面积与圆的半径.其中,是函数关系的是
(填序号)
①③
四、典型例题
例2.汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
解:行驶路程x是自变量,油箱中的油量y是x的函数,
根据题意,每行程x,耗油0.1x,即总油量减少0.1x,
则油箱中的油剩下50-0.1x,
∴y与x的函数关系式为:y=50-0.1x;
四、典型例题
例2.汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(2)指出自变量x的取值范围;
解:因为x代表的实际意义为行驶路程,所以x不能为负数,即x≥0;
又因为行驶中的耗油量为0.1x,不能超过油箱中现有汽油量的值50,
即0.1x≤50,解得,x≤500.
综上所述,自变量x的取值范围是0≤x≤500;
注意:确定自变量的取值范围时,不仅要考虑使函数关系式有意义,而且还要注意问题的实际意义.
四、典型例题
例2.汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(3)汽车行驶200 km时,油箱中还有多少油?
解:汽车行驶200 km时,油箱中的汽油量是函数y=50-0.1x在x=200时的函数值.
将x=200代入y=50-0.1x,得:
y=50-0.1×200=30.
所以,汽车行驶200km时,油箱中还有30L汽油.
四、典型例题
归纳总结:
像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
【当堂检测】
3.写出下列问题中的函数解析式:
(1)图书馆现有1500本图书供学生借阅,如果每个学生一次借3本,则剩下的数y(本)和借书学生人数x(人)之间的函数关系式是_____________.
(2)正方形的边长为5,若边长增加x,则面积增加y,y与x的关系式为_________.
y=x2+10x
y=1500-3x
【当堂检测】
4.一批机器需要零件200个,每天加工20个.若设剩余量为y(个),加工天数为x(天).
(1)求y(个)随x(天)变化的函数表达式;
(2)求自变量x的取值范围;
(3)当剩余零件为120个时,加工了多少天?
解:(1)由剩余量等于总量减加工的量,得:y=-20x+200;
(2)由剩余量是非负数,得-20x+200≥0,
解得x≤10,
由加工的天数是非负数,得x≥0,
所以自变量x的取值范围为0≤x≤10;
(3)当y=120时,200-20x=120,
解得x=4,
即当剩余零件为120个时,加工了4天.
五、课堂总结
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
1.函数:
2.函数值:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
3.函数解析式:
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
第十九章 一次函数
19.1.1 变量与函数
第2课时
1.了解函数的相关概念,会判断两个变量是否具有函数关系.
2.能根据简单的实际问题写出函数解析式,并确定自变量的取值范围.
3.会根据函数解析式求函数值.
一、学习目标
二、新课导入
思考1:下图是体检时的心电图.其中横坐标x表示时间,纵坐标y表示心脏部位的生物电流,它们是两个变量.在心电图中,对于x的每个确定的值,y都有唯一确定的对应值吗
对于x的每个确定值,y都有唯一确定的值与其对应.
二、新课导入
思考2:在下面的我国人口数统计表中,年份与人口数可以记作两个变量x与y,对于表中每一个确定的年份(x),都对应着一个确定的人口数(y)吗
年份
人口数/亿
1984
10.34
1989
11.06
1994
11.76
1999
12.52
2010
13.71
对于表中每个确定的年份x,都对应着一个确定的人口数y.
三、概念剖析
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
(一)函数
例:前面的思考,在心电图中,时间x是自变量,心脏部位的生物电流y是x的函数;
在人口统计表中,年份x是自变量,人口数y是x的函数.
三、概念剖析
(二)函数值
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
例:在人口统计表中,当x=2010时,函数值y=13.71.
四、典型例题
例1.观察并判断下列式子中的y是x的函数吗?为什么?
(1)y=3x﹣5; (2)y= ; (3)x﹣y2=0;
解:(1)y是x的函数,
y=3x﹣5满足对于x的每一个取值,y都有唯一确定的值与之对应关系;
(2)y是x的函数,
满足对于x的每一个取值,y都有唯一确定的值与之对应关系;
(3)y不是x的函数,
x﹣y2=0即y2=x,当x=4时,y=2或﹣2,不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,y不是x的函数.
四、典型例题
(4)y= ; (5)|y|=x.
(4)y是x的函数,
满足对于x的每一个取值,y都有唯一确定的值与之对应关系;
(5)y不是x的函数,
当x=4时,y=4或﹣4,不满足对于x的每一个取值,y都有唯一确定的值与之对应关系,y不是x的函数.
【当堂检测】
1.下列式子中,y不是x的函数的是( )
A.y=-x+3 B. C. D.y=-x
B
【当堂检测】
2.在下列关系式中:①长方形的宽一定时,其长与面积的关系;②等腰三角形的底边长与面积;③圆的面积与圆的半径.其中,是函数关系的是
(填序号)
①③
四、典型例题
例2.汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(1)写出表示y与x的函数关系的式子.
解:行驶路程x是自变量,油箱中的油量y是x的函数,
根据题意,每行程x,耗油0.1x,即总油量减少0.1x,
则油箱中的油剩下50-0.1x,
∴y与x的函数关系式为:y=50-0.1x;
四、典型例题
例2.汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(2)指出自变量x的取值范围;
解:因为x代表的实际意义为行驶路程,所以x不能为负数,即x≥0;
又因为行驶中的耗油量为0.1x,不能超过油箱中现有汽油量的值50,
即0.1x≤50,解得,x≤500.
综上所述,自变量x的取值范围是0≤x≤500;
注意:确定自变量的取值范围时,不仅要考虑使函数关系式有意义,而且还要注意问题的实际意义.
四、典型例题
例2.汽车的油箱中有汽油50L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程x(单位:km)的增加而减少,平均耗油量为0.1L/km.
(3)汽车行驶200 km时,油箱中还有多少油?
解:汽车行驶200 km时,油箱中的汽油量是函数y=50-0.1x在x=200时的函数值.
将x=200代入y=50-0.1x,得:
y=50-0.1×200=30.
所以,汽车行驶200km时,油箱中还有30L汽油.
四、典型例题
归纳总结:
像y=50-0.1x这样,用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
【当堂检测】
3.写出下列问题中的函数解析式:
(1)图书馆现有1500本图书供学生借阅,如果每个学生一次借3本,则剩下的数y(本)和借书学生人数x(人)之间的函数关系式是_____________.
(2)正方形的边长为5,若边长增加x,则面积增加y,y与x的关系式为_________.
y=x2+10x
y=1500-3x
【当堂检测】
4.一批机器需要零件200个,每天加工20个.若设剩余量为y(个),加工天数为x(天).
(1)求y(个)随x(天)变化的函数表达式;
(2)求自变量x的取值范围;
(3)当剩余零件为120个时,加工了多少天?
解:(1)由剩余量等于总量减加工的量,得:y=-20x+200;
(2)由剩余量是非负数,得-20x+200≥0,
解得x≤10,
由加工的天数是非负数,得x≥0,
所以自变量x的取值范围为0≤x≤10;
(3)当y=120时,200-20x=120,
解得x=4,
即当剩余零件为120个时,加工了4天.
五、课堂总结
一般地,在一个变化过程中,如果有两个变量x和y,并且对于x的每一个确定的值,y都有唯一确定的值与其对应,那么我们就说x是自变量,y是x的函数.
1.函数:
2.函数值:
如果当x=a时y=b,那么b叫做当自变量的值为a时的函数值.
3.函数解析式:
用关于自变量的数学式子表示函数与自变量之间的关系,是描述函数的常用方法.这种式子叫做函数的解析式.
