19.1.2 函数的图象 第1课时 课件(共14张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.1.2 函数的图象 第1课时 课件(共14张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 323.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 10:52:52 | ||
图片预览






文档简介
(共14张PPT)
第十九章 一次函数
19.1.2 函数的图象
第1课时
1.知道用列表和直角坐标系中的点表示函数两个变量的对应关系
2.能从函数图象中获取函数的相关信息
3.明确用描点法画函数图象的一般步骤,会画函数的图象
一、学习目标
二、新课导入
复习回顾
1.下列各式中,请判断y是不是x的函数,并说一说理由.
(1)y=2x; (2)y2=x; (3)y=|x|
思考:函数除了用解析式表示以外,还可以用图象来表示,那么什么是函数的图象呢?
解:(1)(3)式中y是x的函数,它们都满足对于x的每一个取值,y都有唯一确定的值与之对应关系;
(2)式中y不是x的函数,当x=4时,y=2或-2,不满足对于x的每一个取值,y都有唯一确定的值与之对应关系.
三、概念剖析
(一)函数的图象
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
怎么画出一个函数的图象呢?
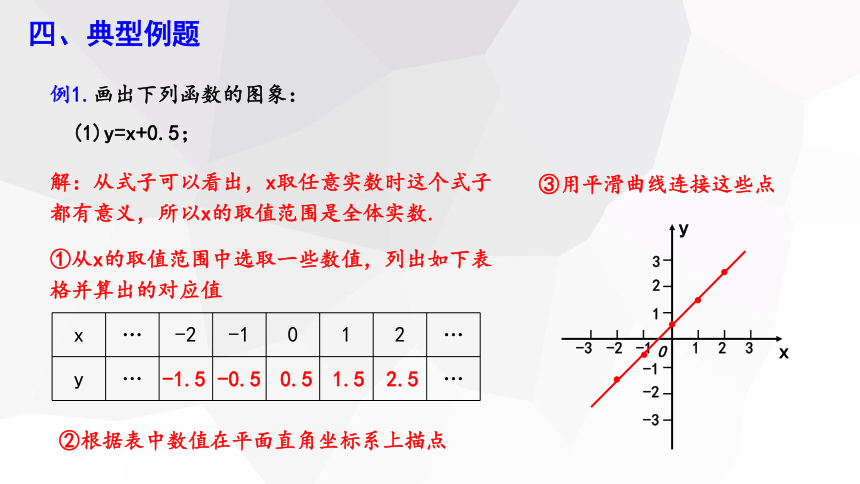
例1.画出下列函数的图象:
(1)y=x+0.5;
解:从式子可以看出,x取任意实数时这个式子都有意义,所以x的取值范围是全体实数.
①从x的取值范围中选取一些数值,列出如下表格并算出的对应值
x … -2 -1 0 1 2 …
y … …
-1.5
-0.5
0.5
1.5
2.5
②根据表中数值在平面直角坐标系上描点
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
③用平滑曲线连接这些点
四、典型例题
解:自变量x>0
①从x的取值范围中选取一些数值,列表
x … 1 2 3 4 …
y … …
6
3
2
1.5
②根据表中数值在平面直角坐标系上描点
③用平滑曲线连接这些点
例1.画出下列函数的图象:
(2)
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
四、典型例题
归纳总结:
(1)列表:表中给出一些自变量的值及其对应的函数值;
(2)描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点;
(3)连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
描点法画函数图象的一般步骤如下:
注意:表示x与y的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同时想象出其他点的位置.
四、典型例题
1.画出函数y=x+1的图象
解:由函数关系式可知自变量x的取值范围是全体实数.
(1)列表:
x … -2 0 2 …
y … …
1
-1
3
(2)描点:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
(3)连线:
【当堂检测】
例2.请观察函数图象,完成问题.汽车在行驶的过程中速度往往是变化的,图表示一辆汽车的速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多长时间?它的最高速度是多少?
四、典型例题
汽车从出发到最后停止共经历了24 min,
它的最高速度是90 km/h.
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
汽车在2 min到6 min,18 min到22 min时间段保持匀速行驶,
速度分别是30 km/h和90 km/h.
(3)汽车出发后8 min到10 min之间可能发生了什么情况?
此时汽车处于静止状态,可能是遇到红灯等情况(回答只要合理即可)
四、典型例题
(4)请你描述汽车行驶的整个过程.
0~2 min,发动汽车做加速行驶;
2~6 min以30 km/h的速度匀速行驶;
6~8 min,由于某些状况,开始减速慢行;
8~10 min,汽车静止;
10~18 min,又开始加速行驶;
18~22 min,以90 km/h的速度匀速行驶;
22~24 min,减速行驶到达目的地.
四、典型例题
2.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )
A.小明中途休息用了20分钟
B.小明在上述过程中所走路程为7200米
C.小明休息前爬山的速度为每分钟60米
D.小明休息前后爬山的平均速度相等
【当堂检测】
B
3.如图是某港口在某天从0时到12时的水位情况变化曲线.
(1)在这一问题中,自变量是什么?
(2)大约在什么时间水位最深,最深是多少?
(3)大约在什么时间段水位是随着时间推移不断上涨的?
【当堂检测】
解:(1)由图像可知,自变量是时间;
(2)大约在3时水位最深,最深是8米;
(3)由图像可得,在0到3时和9时到12时,水位是随着时间推移不断上涨的.
五、课堂总结
1.函数的图象
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
(1)列表:表中给出一些自变量的值及其对应的函数值;
(2)描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点;
(3)连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
2.描点法画函数图像的一般步骤:
第十九章 一次函数
19.1.2 函数的图象
第1课时
1.知道用列表和直角坐标系中的点表示函数两个变量的对应关系
2.能从函数图象中获取函数的相关信息
3.明确用描点法画函数图象的一般步骤,会画函数的图象
一、学习目标
二、新课导入
复习回顾
1.下列各式中,请判断y是不是x的函数,并说一说理由.
(1)y=2x; (2)y2=x; (3)y=|x|
思考:函数除了用解析式表示以外,还可以用图象来表示,那么什么是函数的图象呢?
解:(1)(3)式中y是x的函数,它们都满足对于x的每一个取值,y都有唯一确定的值与之对应关系;
(2)式中y不是x的函数,当x=4时,y=2或-2,不满足对于x的每一个取值,y都有唯一确定的值与之对应关系.
三、概念剖析
(一)函数的图象
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
怎么画出一个函数的图象呢?
例1.画出下列函数的图象:
(1)y=x+0.5;
解:从式子可以看出,x取任意实数时这个式子都有意义,所以x的取值范围是全体实数.
①从x的取值范围中选取一些数值,列出如下表格并算出的对应值
x … -2 -1 0 1 2 …
y … …
-1.5
-0.5
0.5
1.5
2.5
②根据表中数值在平面直角坐标系上描点
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
③用平滑曲线连接这些点
四、典型例题
解:自变量x>0
①从x的取值范围中选取一些数值,列表
x … 1 2 3 4 …
y … …
6
3
2
1.5
②根据表中数值在平面直角坐标系上描点
③用平滑曲线连接这些点
例1.画出下列函数的图象:
(2)
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
四、典型例题
归纳总结:
(1)列表:表中给出一些自变量的值及其对应的函数值;
(2)描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点;
(3)连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
描点法画函数图象的一般步骤如下:
注意:表示x与y的对应关系的点有无数个.但是实际上我们只能描出其中有限个点,同时想象出其他点的位置.
四、典型例题
1.画出函数y=x+1的图象
解:由函数关系式可知自变量x的取值范围是全体实数.
(1)列表:
x … -2 0 2 …
y … …
1
-1
3
(2)描点:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
(3)连线:
【当堂检测】
例2.请观察函数图象,完成问题.汽车在行驶的过程中速度往往是变化的,图表示一辆汽车的速度随时间变化而变化的情况.
(1)汽车从出发到最后停止共经过了多长时间?它的最高速度是多少?
四、典型例题
汽车从出发到最后停止共经历了24 min,
它的最高速度是90 km/h.
(2)汽车在哪些时间段保持匀速行驶?时速分别是多少?
汽车在2 min到6 min,18 min到22 min时间段保持匀速行驶,
速度分别是30 km/h和90 km/h.
(3)汽车出发后8 min到10 min之间可能发生了什么情况?
此时汽车处于静止状态,可能是遇到红灯等情况(回答只要合理即可)
四、典型例题
(4)请你描述汽车行驶的整个过程.
0~2 min,发动汽车做加速行驶;
2~6 min以30 km/h的速度匀速行驶;
6~8 min,由于某些状况,开始减速慢行;
8~10 min,汽车静止;
10~18 min,又开始加速行驶;
18~22 min,以90 km/h的速度匀速行驶;
22~24 min,减速行驶到达目的地.
四、典型例题
2.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间,设他从山脚出发后所用时间为t(分钟),所走路程为s(米),s与t之间的函数关系如图所示,则下列说法中,错误的是( )
A.小明中途休息用了20分钟
B.小明在上述过程中所走路程为7200米
C.小明休息前爬山的速度为每分钟60米
D.小明休息前后爬山的平均速度相等
【当堂检测】
B
3.如图是某港口在某天从0时到12时的水位情况变化曲线.
(1)在这一问题中,自变量是什么?
(2)大约在什么时间水位最深,最深是多少?
(3)大约在什么时间段水位是随着时间推移不断上涨的?
【当堂检测】
解:(1)由图像可知,自变量是时间;
(2)大约在3时水位最深,最深是8米;
(3)由图像可得,在0到3时和9时到12时,水位是随着时间推移不断上涨的.
五、课堂总结
1.函数的图象
一般地,对于一个函数,如果把自变量与函数的每对对应值分别作为点的横、纵坐标,那么坐标平面内由这些点组成的图形,就是这个函数的图象.
(1)列表:表中给出一些自变量的值及其对应的函数值;
(2)描点:在直角坐标系中,以自变量的值为横坐标,相应的函数值为纵坐标,描出表格中的数值对应的各点;
(3)连线:按照横坐标由小到大的顺序,把所描出的各点用平滑曲线连接起来.
2.描点法画函数图像的一般步骤:
