19.2.1 正比例函数 第2课时 课件(共17张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.2.1 正比例函数 第2课时 课件(共17张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 167.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 11:30:10 | ||
图片预览




文档简介
(共17张PPT)
第十九章 一次函数
19.2.1 正比例函数
第2课时
1.会利用两点(法)画正比例函数的图象
2.通过观察不同的正比例函数图象,总结正比例函数的性质
一、学习目标
二、新课导入
复习回顾
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
2.你还记得描点法画函数图像的步骤吗?
列表、描点、连线
1.什么是正比例函数?
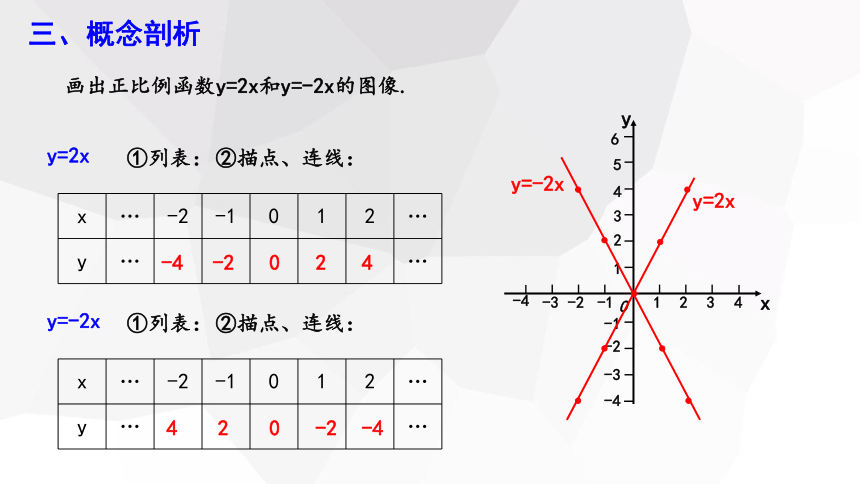
画出正比例函数y=2x和y=-2x的图像.
y=2x
①列表:
x … -2 -1 0 1 2 …
y … …
-4
-2
0
2
4
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
-4
-4
y=2x
②描点、连线:
y=-2x
①列表:
x … -2 -1 0 1 2 …
y … …
4
2
0
-2
-4
②描点、连线:
y=-2x
三、概念剖析
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
-4
-4
y=2x
y=-2x
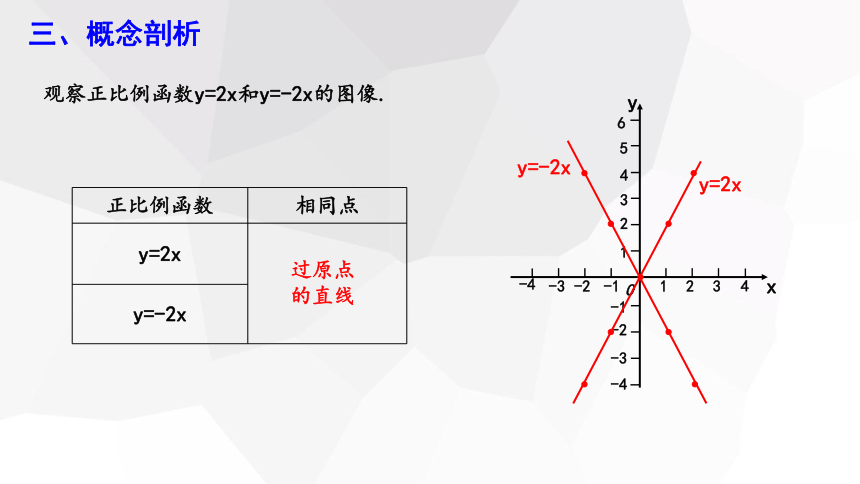
观察正比例函数y=2x和y=-2x的图像.
正比例函数 相同点
y=2x
y=-2x
过原点的直线
三、概念剖析
三、概念剖析
1.正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线.
2.因为两点确定一条直线,所以可用两点法画正比例函数y=kx(k≠0)的图像.一般地,过原点和点(1,k)(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的图像.
归纳:
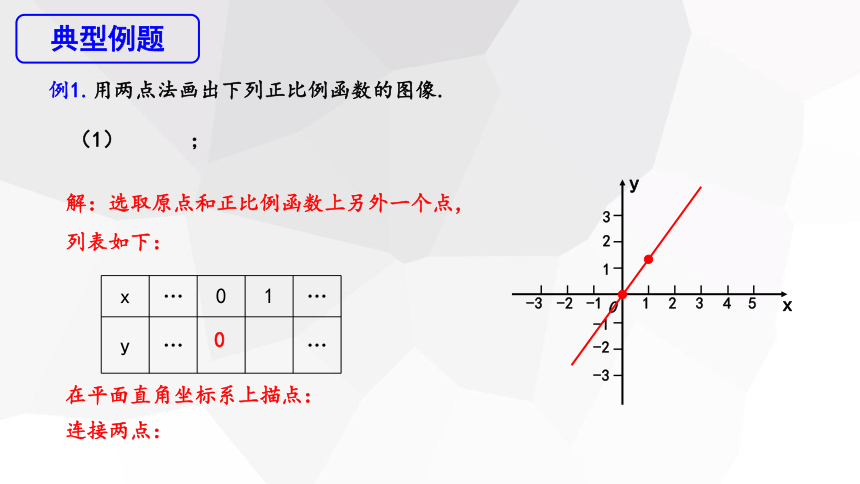
例1.用两点法画出下列正比例函数的图像.
(1) ;
解:选取原点和正比例函数上另外一个点,
列表如下:
x … 0 1 …
y … …
0
在平面直角坐标系上描点:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
连接两点:
典型例题
例1.用两点法画出下列正比例函数的图像.
(2)y=-1.5x
解:选取原点和正比例函数上另外一个点,
列表如下:
x … 0 1 …
y … …
0
在平面直角坐标系上描点:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
连接两点:
-1.5
y=-1.5x
典型例题
两点作图法:
两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k)(k是常数,k≠0),连线即可.
典型例题
【当堂检测】
1.用你认为最简单的方法画出下列函数的图像:
(1) ; (2)y=x
x … 0 1 …
… …
y=x … …
0
0
1
解:选取原点和正比例函数上另外一个点,
列表如下:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
y=x
描点、连线:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
-4
-4
y=2x
y=-2x
观察正比例函数y=2x和y=-2x图像不同之处.
正比例函数 不同点
y=2x
y=-2x
过一、三象限,直线从左往右上升
过二、四象限,直线从左往右下降
三、概念剖析
性质:正比例函数y=kx(k是常数,k≠0)的图象,当k>0时,直线经过第一、三象限,y随x的增大而增大;当k<0时,直线经过第二、四象限,y随x的增大而减小.
例2.已知正比例函数y=(m-3)x
(1)若y随着x的增大而减小,求m的取值范围;
分析:当k<0时,函数图像经过二、四象限,即随着x的增大y反而减小.
典型例题
解:∵正比例函数y=(m-3)x中,y随x的增大而减小
∴m-3<0,
解得:m<3
例2.已知正比例函数y=(m-3)x
(2)若函数图象经过第一、三象限,试求m的取值范围.
分析:当k>0时,函数图像经过一、三象限,即随着x的增大y也增大.
典型例题
解:∵正比例函数y=(m-3)x的图象经过第一、三象限
∴m-3>0,
解得:m>3
典型例题
例3.点A(-1, )和B(1, )都在直线y=ax(a>0)上,试判断 和 的大小.
解:由直线y=ax(a>0)可知,正比例函数y随x的增大而增大,
∵ -1<1,
∴ < .
分析:根据观察a>0,可知正比例函数y=ax(a>0)的图像经过一、三象限且直线从左往右上升,再通过比较-1与1的大小即可得出.
【当堂检测】
2.点A(5, )和B(2, )都在直线y=-x上,则 与 的关系是( )
A. ≥ B. =
C. < D. >
C
【当堂检测】
3.已知关于x的正比例函数y=(5-2k)x.
(1)当k取何值时,y随x的增大而增大.
(2)当k取何值时,y随x的增大而减小.
解:(1)当5-2k>0时,
k< ,
∴当 时,y随x的增大而增大.
k<
(2)当5-2k<0时,
k> ,
∴当 时,y随x的增大而减小.
k>
四、课堂总结
1.正比例函数的图像
3.正比例函数的性质
正比例函数y=kx(k是常数,k≠0)的图象,当k>0时,直线经过第一、三象限,y随x的增大而增大;当k<0时,直线经过第二、四象限,y随x的增大而减小.
正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线.
2.两点作图法:
两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k)(k是常数,k≠0),连线即可.
第十九章 一次函数
19.2.1 正比例函数
第2课时
1.会利用两点(法)画正比例函数的图象
2.通过观察不同的正比例函数图象,总结正比例函数的性质
一、学习目标
二、新课导入
复习回顾
一般地,形如y=kx(k是常数,k≠0)的函数,叫做正比例函数,其中k叫做比例系数.
2.你还记得描点法画函数图像的步骤吗?
列表、描点、连线
1.什么是正比例函数?
画出正比例函数y=2x和y=-2x的图像.
y=2x
①列表:
x … -2 -1 0 1 2 …
y … …
-4
-2
0
2
4
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
-4
-4
y=2x
②描点、连线:
y=-2x
①列表:
x … -2 -1 0 1 2 …
y … …
4
2
0
-2
-4
②描点、连线:
y=-2x
三、概念剖析
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
-4
-4
y=2x
y=-2x
观察正比例函数y=2x和y=-2x的图像.
正比例函数 相同点
y=2x
y=-2x
过原点的直线
三、概念剖析
三、概念剖析
1.正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线.
2.因为两点确定一条直线,所以可用两点法画正比例函数y=kx(k≠0)的图像.一般地,过原点和点(1,k)(k是常数,k≠0)的直线,即正比例函数y=kx(k≠0)的图像.
归纳:
例1.用两点法画出下列正比例函数的图像.
(1) ;
解:选取原点和正比例函数上另外一个点,
列表如下:
x … 0 1 …
y … …
0
在平面直角坐标系上描点:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
连接两点:
典型例题
例1.用两点法画出下列正比例函数的图像.
(2)y=-1.5x
解:选取原点和正比例函数上另外一个点,
列表如下:
x … 0 1 …
y … …
0
在平面直角坐标系上描点:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
连接两点:
-1.5
y=-1.5x
典型例题
两点作图法:
两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k)(k是常数,k≠0),连线即可.
典型例题
【当堂检测】
1.用你认为最简单的方法画出下列函数的图像:
(1) ; (2)y=x
x … 0 1 …
… …
y=x … …
0
0
1
解:选取原点和正比例函数上另外一个点,
列表如下:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
y=x
描点、连线:
x
y
1
2
3
-2
-1
-3
1
2
3
-2
-1
-3
O
4
5
6
4
-4
-4
y=2x
y=-2x
观察正比例函数y=2x和y=-2x图像不同之处.
正比例函数 不同点
y=2x
y=-2x
过一、三象限,直线从左往右上升
过二、四象限,直线从左往右下降
三、概念剖析
性质:正比例函数y=kx(k是常数,k≠0)的图象,当k>0时,直线经过第一、三象限,y随x的增大而增大;当k<0时,直线经过第二、四象限,y随x的增大而减小.
例2.已知正比例函数y=(m-3)x
(1)若y随着x的增大而减小,求m的取值范围;
分析:当k<0时,函数图像经过二、四象限,即随着x的增大y反而减小.
典型例题
解:∵正比例函数y=(m-3)x中,y随x的增大而减小
∴m-3<0,
解得:m<3
例2.已知正比例函数y=(m-3)x
(2)若函数图象经过第一、三象限,试求m的取值范围.
分析:当k>0时,函数图像经过一、三象限,即随着x的增大y也增大.
典型例题
解:∵正比例函数y=(m-3)x的图象经过第一、三象限
∴m-3>0,
解得:m>3
典型例题
例3.点A(-1, )和B(1, )都在直线y=ax(a>0)上,试判断 和 的大小.
解:由直线y=ax(a>0)可知,正比例函数y随x的增大而增大,
∵ -1<1,
∴ < .
分析:根据观察a>0,可知正比例函数y=ax(a>0)的图像经过一、三象限且直线从左往右上升,再通过比较-1与1的大小即可得出.
【当堂检测】
2.点A(5, )和B(2, )都在直线y=-x上,则 与 的关系是( )
A. ≥ B. =
C. < D. >
C
【当堂检测】
3.已知关于x的正比例函数y=(5-2k)x.
(1)当k取何值时,y随x的增大而增大.
(2)当k取何值时,y随x的增大而减小.
解:(1)当5-2k>0时,
k< ,
∴当 时,y随x的增大而增大.
k<
(2)当5-2k<0时,
k> ,
∴当 时,y随x的增大而减小.
k>
四、课堂总结
1.正比例函数的图像
3.正比例函数的性质
正比例函数y=kx(k是常数,k≠0)的图象,当k>0时,直线经过第一、三象限,y随x的增大而增大;当k<0时,直线经过第二、四象限,y随x的增大而减小.
正比例函数y=kx(k是常数,k≠0)的图象是一条经过原点的直线.
2.两点作图法:
两点确定一条直线,画正比例函数图象时我们只需描点(0,0)和点 (1,k)(k是常数,k≠0),连线即可.
