19.2.3 一次函数与方程、不等式 第1课时 课件(共16张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 19.2.3 一次函数与方程、不等式 第1课时 课件(共16张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 163.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 11:37:17 | ||
图片预览






文档简介
(共16张PPT)
第十九章 一次函数
19.2.3 一次函数与方程、不等式
第1课时
1.结合一次函数图象,理解并掌握一次函数与一元一次方程、一元一次不等式的相互联系
2.能通过函数图象来求一元一次方程的解和一元一次不等式的解集
一、学习目标
二、新课导入
复习回顾
1.一次函数的一般形式是什么?
y=kx+b(k、b是常数,k≠0)
2.把一次函数中的变量y换为0,那么函数变成了什么式子呢?
一元一次方程
思考:一次函数与一元一次方程之间有什么联系呢?
kx+b=0(k≠0),
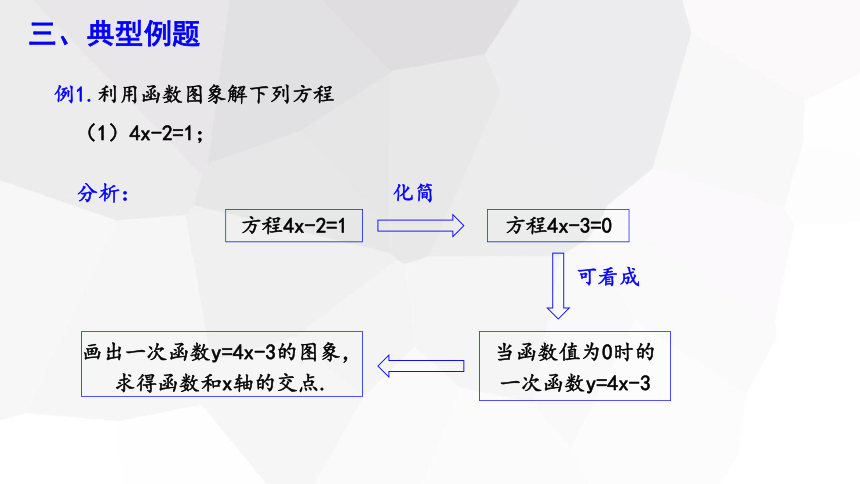
例1.利用函数图象解下列方程
(1)4x-2=1;
三、典型例题
分析:
方程4x-2=1
当函数值为0时的一次函数y=4x-3
化简
方程4x-3=0
可看成
画出一次函数y=4x-3的图象,求得函数和x轴的交点.
例1.利用函数图象解下列方程
(1)4x-2=1;
三、典型例题
解:方程4x-2=1,
化简,得:4x-3=0,
画函数y=4x-3的图象,如图所示,
由图象可知直线y=4x-3交x轴于点(0.75,0),
故方程4x-3=0的解是x=0.75,
从而可知原方程的解为x=0.75.
y=4x-3
函数y=4x-3可分别取当x=0时y的值和当y=0时x的值,两个点画直线
例1.利用函数图象解下列方程
(2)3x-2=x+4.
三、典型例题
解:方程化简,得:2x-6=0,
画函数y=2x-6的图象,如图所示,
由图象可知直线y=2x-6交x轴于点(3,0),
故方程2x-6=0的解是x=3,
从而可知原方程的解为x=3.
y=2x-6
归纳总结:
三、典型例题
所有的一元一次方程都可以化为ax+b=0(a≠0)的形式,解一元一次方程ax+b=0相当于一次函数y=ax+b的函数值为0时(即与x轴的交点),求自变量x的值.
1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A. x=2 B. x=0
C. x=-1 D. x=-3
D
分析:∵直线y=ax+b过点B(-3,0),
∴方程ax+b=0的解是x=-3.
【当堂检测】
∴直线y=ax+b与x轴的交点的横坐标为-3,
2.利用图象法解方程:2x-4=0.
解:画出直线y=2x-4的图象,如右图
O
x
y
-4
2
y=2x-4
·
·
【当堂检测】
从函数图象上可以看出直线y=2x-4与x轴的交点坐标是(2,0),
∴方程2x-4=0的解是x=2
三、典型例题
例2.画出函数y=- x+3的图象,并利用图象解下列问题:
(1)求方程- x+3=0的解;
分析:先利用描点法画出一次函数图象,然后利用直线与x轴的交点坐标确定
方程- x+3=0的解;
解:函数 的图象如右图所示:
∵直线与x轴的交点坐标为(2,0),
∴方程 的解为x=2;
三、典型例题
例2.画出函数y=- x+3的图象,并利用图象解下列问题:
(2)求不等式- x+3>0的解集;
分析:结合函数图象观察x轴上方所对应的自变量的范围,确定不等式的解集;
解:观察函数 的图象,
∵x<2时,y>0,
∴x<2时,不等式 >0,
∴不等式 >0的解集为x<2;
三、典型例题
分析:结合函数图象观察x轴下方所对应的自变量的范围,确定不等式的解集.
即 <0,
∴不等式 <0的解集为x>2.
解:观察函数 的图象,
当x>2时,y<0,
例2.画出函数y=- x+3的图象,并利用图象解下列问题:
(3)求不等式- x+3<0的解集.
归纳总结:
三、典型例题
因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b的函数值大于0或小于0时,求自变量x的取值范围.
3.如图,直线y=kx+b(b>0)经过点(2,0),则关于x的不等式kx+b≥0的解集是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
【当堂检测】
D
4.在坐标系中作出函数y=2x+6的图象,利用图象解答下列问题:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>4的解集.
【当堂检测】
y=2x+6
解:函数y=2x+6的图象如右图所示:
(1)∵直线与x轴的交点坐标为(-3,0),
∴方程2x+6=0的解为x=-3;
(2)观察图象可知,直线经过点(-1,4),
所以不等式2x+6>4的解集为x>-1;
当x>-1时,y>4,
四、课堂总结
所有的一元一次方程都可以化为ax+b=0(a≠0)的形式,解一元一次方程ax+b=0相当于一次函数y=ax+b的函数值为0时(即与x轴的交点),求自变量x的值.
1.一次函数与一元一次方程
2.一次函数与一元一次不等式
因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b的函数值大于0或小于0时,求自变量x的取值范围.
第十九章 一次函数
19.2.3 一次函数与方程、不等式
第1课时
1.结合一次函数图象,理解并掌握一次函数与一元一次方程、一元一次不等式的相互联系
2.能通过函数图象来求一元一次方程的解和一元一次不等式的解集
一、学习目标
二、新课导入
复习回顾
1.一次函数的一般形式是什么?
y=kx+b(k、b是常数,k≠0)
2.把一次函数中的变量y换为0,那么函数变成了什么式子呢?
一元一次方程
思考:一次函数与一元一次方程之间有什么联系呢?
kx+b=0(k≠0),
例1.利用函数图象解下列方程
(1)4x-2=1;
三、典型例题
分析:
方程4x-2=1
当函数值为0时的一次函数y=4x-3
化简
方程4x-3=0
可看成
画出一次函数y=4x-3的图象,求得函数和x轴的交点.
例1.利用函数图象解下列方程
(1)4x-2=1;
三、典型例题
解:方程4x-2=1,
化简,得:4x-3=0,
画函数y=4x-3的图象,如图所示,
由图象可知直线y=4x-3交x轴于点(0.75,0),
故方程4x-3=0的解是x=0.75,
从而可知原方程的解为x=0.75.
y=4x-3
函数y=4x-3可分别取当x=0时y的值和当y=0时x的值,两个点画直线
例1.利用函数图象解下列方程
(2)3x-2=x+4.
三、典型例题
解:方程化简,得:2x-6=0,
画函数y=2x-6的图象,如图所示,
由图象可知直线y=2x-6交x轴于点(3,0),
故方程2x-6=0的解是x=3,
从而可知原方程的解为x=3.
y=2x-6
归纳总结:
三、典型例题
所有的一元一次方程都可以化为ax+b=0(a≠0)的形式,解一元一次方程ax+b=0相当于一次函数y=ax+b的函数值为0时(即与x轴的交点),求自变量x的值.
1.如图,直线y=ax+b过点A(0,2)和点B(-3,0),则方程ax+b=0的解是( )
A. x=2 B. x=0
C. x=-1 D. x=-3
D
分析:∵直线y=ax+b过点B(-3,0),
∴方程ax+b=0的解是x=-3.
【当堂检测】
∴直线y=ax+b与x轴的交点的横坐标为-3,
2.利用图象法解方程:2x-4=0.
解:画出直线y=2x-4的图象,如右图
O
x
y
-4
2
y=2x-4
·
·
【当堂检测】
从函数图象上可以看出直线y=2x-4与x轴的交点坐标是(2,0),
∴方程2x-4=0的解是x=2
三、典型例题
例2.画出函数y=- x+3的图象,并利用图象解下列问题:
(1)求方程- x+3=0的解;
分析:先利用描点法画出一次函数图象,然后利用直线与x轴的交点坐标确定
方程- x+3=0的解;
解:函数 的图象如右图所示:
∵直线与x轴的交点坐标为(2,0),
∴方程 的解为x=2;
三、典型例题
例2.画出函数y=- x+3的图象,并利用图象解下列问题:
(2)求不等式- x+3>0的解集;
分析:结合函数图象观察x轴上方所对应的自变量的范围,确定不等式的解集;
解:观察函数 的图象,
∵x<2时,y>0,
∴x<2时,不等式 >0,
∴不等式 >0的解集为x<2;
三、典型例题
分析:结合函数图象观察x轴下方所对应的自变量的范围,确定不等式的解集.
即 <0,
∴不等式 <0的解集为x>2.
解:观察函数 的图象,
当x>2时,y<0,
例2.画出函数y=- x+3的图象,并利用图象解下列问题:
(3)求不等式- x+3<0的解集.
归纳总结:
三、典型例题
因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b的函数值大于0或小于0时,求自变量x的取值范围.
3.如图,直线y=kx+b(b>0)经过点(2,0),则关于x的不等式kx+b≥0的解集是( )
A.x>2 B.x<2 C.x≥2 D.x≤2
【当堂检测】
D
4.在坐标系中作出函数y=2x+6的图象,利用图象解答下列问题:
(1)求方程2x+6=0的解;
(2)求不等式2x+6>4的解集.
【当堂检测】
y=2x+6
解:函数y=2x+6的图象如右图所示:
(1)∵直线与x轴的交点坐标为(-3,0),
∴方程2x+6=0的解为x=-3;
(2)观察图象可知,直线经过点(-1,4),
所以不等式2x+6>4的解集为x>-1;
当x>-1时,y>4,
四、课堂总结
所有的一元一次方程都可以化为ax+b=0(a≠0)的形式,解一元一次方程ax+b=0相当于一次函数y=ax+b的函数值为0时(即与x轴的交点),求自变量x的值.
1.一次函数与一元一次方程
2.一次函数与一元一次不等式
因为任何一个以x为未知数的一元一次不等式都可以变形为ax+b>0或ax+b<0(a≠0)的形式,所以解一元一次不等式相当于在某个一次函数y=ax+b的函数值大于0或小于0时,求自变量x的取值范围.
