20.2 数据的波动程度 第1课时 课件(共15张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 20.2 数据的波动程度 第1课时 课件(共15张PPT) 2023-2024学年初中数学人教版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 489.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 12:02:02 | ||
图片预览





文档简介
(共15张PPT)
第二十章 数据的分析
20.2 数据的波动程度
第1课时
1.知道方差的概念和计算公式,会用方差来比较两组数据的波动大小.
2.会用科学计算器计算一组数据的方差,并根据计算结果对实际问题作出评判.
一、学习目标
二、新课导入
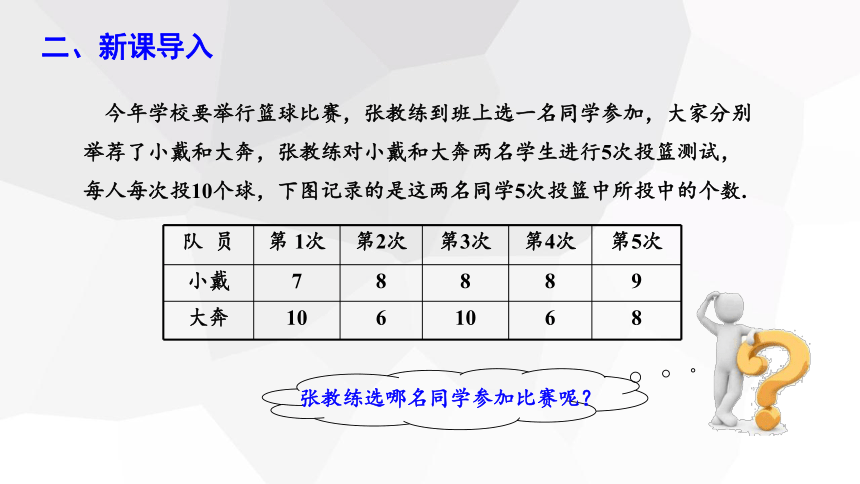
今年学校要举行篮球比赛,张教练到班上选一名同学参加,大家分别举荐了小戴和大奔,张教练对小戴和大奔两名学生进行5次投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
队 员 第 1次 第2次 第3次 第4次 第5次
小戴 7 8 8 8 9
大奔 10 6 10 6 8
张教练选哪名同学参加比赛呢?
三、概念剖析
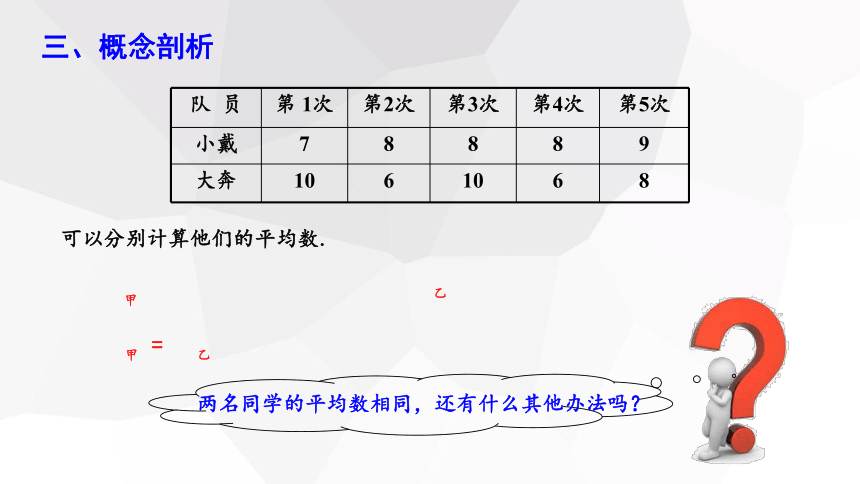
队 员 第 1次 第2次 第3次 第4次 第5次
小戴 7 8 8 8 9
大奔 10 6 10 6 8
可以分别计算他们的平均数.
甲
乙
甲
乙
=
两名同学的平均数相同,还有什么其他办法吗?
可以分别计算他们的方差.
三、概念剖析
什么是方差呢?
设有n个数据x1、x2、...、xn,
各数据与它们的平均数 的差的平方分别是 、 、...、 ,
方差衡量数据波动的大小即数据偏离平均数的大小,记做s2.
s甲2=
队 员 第 1次 第2次 第3次 第4次 第5次
小戴 7 8 8 8 9
大奔 10 6 10 6 8
三、概念剖析
s乙2=
s甲2<s乙2
方差的大小与数据的波动有什么关系呢?
三、概念剖析
归纳总结
数据在平均数附近波动比较大时(数据分布比较分散),各个数据与平均数的差的平方和较大,即方差就较大;
数据在平均数附近波动比较小时(数据分布比较集中),各个数据与平均数的差的平方和较小,即方差就较小;
例1.在这次篮球联赛中,最后是九班和三班争夺这次篮球赛冠军, 赛前两个班的拉拉队都表演了啦啦操,参加表演的女同学的身高(单位:cm)分别是:
哪班啦啦操队女同学的身高更整齐
九班 163 163 165 165 165 166 166 167
三班 163 164 164 164 165 166 167 167
四、典型例题
s九2=
s三2=
s九2<s三2
九班 163 163 165 165 165 166 166 167
三班 163 164 164 164 165 166 167 167
九
三
所以九班啦啦操队女同学的身高更整齐.
四、典型例题
方法二:
九班 163 163 165 165 165 166 166 167
三班 163 164 164 164 165 166 167 167
取 a = 165,得到九班和三班的新数据如下表所示:
九班 -2 -2 0 0 0 1 1 2
三班 -2 -1 -1 -1 0 1 2 2
九
三
s九2=
s三2=
s九2<s三2
四、典型例题
求一组较大数据的方差,有如下简便计算方法:
四、典型例题
归纳总结
(1)任取一个基准数a
(2)将原数据减去a,得到一组新数据
(3)求新数据的方差
【当堂检测】
分析:根据方差的意义,反映一组数据的波动大小,方差越大,波动性越大.
∵S 甲=24,S 乙=18,∴S 甲>S 乙,
∴乙班成绩较为稳定.
B
1.人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差如下: = =80,S 甲=24,S 乙=18,则成绩较为稳定的班级是( )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
甲
乙
2.甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则 同学(填“甲”或“乙”)的射击成绩更稳定些.
命中环数 7 8 9 10
甲命中相应环数的次数 2 2 0 1
乙命中相应环数的次数 1 3 1 0
乙
【当堂检测】
【当堂检测】
3.甲、乙两台编织机纺织一种毛衣,在5天中两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
解:
=(7+10+8+8+7)÷5=8,
甲
=(8+9+7+9+7)÷5=8,
乙
S 甲>S 乙,乙台编织机出合格品的波动较小.
甲
乙
四、课堂总结
方差
数据在平均数附近波动比较大时(数据分布比较分散),各个数据与平均数的差的平方和较大,即方差就较大;
数据在平均数附近波动比较小时(数据分布比较集中),各个数据与平均数的差的平方和较小,即方差就较小;
第二十章 数据的分析
20.2 数据的波动程度
第1课时
1.知道方差的概念和计算公式,会用方差来比较两组数据的波动大小.
2.会用科学计算器计算一组数据的方差,并根据计算结果对实际问题作出评判.
一、学习目标
二、新课导入
今年学校要举行篮球比赛,张教练到班上选一名同学参加,大家分别举荐了小戴和大奔,张教练对小戴和大奔两名学生进行5次投篮测试,每人每次投10个球,下图记录的是这两名同学5次投篮中所投中的个数.
队 员 第 1次 第2次 第3次 第4次 第5次
小戴 7 8 8 8 9
大奔 10 6 10 6 8
张教练选哪名同学参加比赛呢?
三、概念剖析
队 员 第 1次 第2次 第3次 第4次 第5次
小戴 7 8 8 8 9
大奔 10 6 10 6 8
可以分别计算他们的平均数.
甲
乙
甲
乙
=
两名同学的平均数相同,还有什么其他办法吗?
可以分别计算他们的方差.
三、概念剖析
什么是方差呢?
设有n个数据x1、x2、...、xn,
各数据与它们的平均数 的差的平方分别是 、 、...、 ,
方差衡量数据波动的大小即数据偏离平均数的大小,记做s2.
s甲2=
队 员 第 1次 第2次 第3次 第4次 第5次
小戴 7 8 8 8 9
大奔 10 6 10 6 8
三、概念剖析
s乙2=
s甲2<s乙2
方差的大小与数据的波动有什么关系呢?
三、概念剖析
归纳总结
数据在平均数附近波动比较大时(数据分布比较分散),各个数据与平均数的差的平方和较大,即方差就较大;
数据在平均数附近波动比较小时(数据分布比较集中),各个数据与平均数的差的平方和较小,即方差就较小;
例1.在这次篮球联赛中,最后是九班和三班争夺这次篮球赛冠军, 赛前两个班的拉拉队都表演了啦啦操,参加表演的女同学的身高(单位:cm)分别是:
哪班啦啦操队女同学的身高更整齐
九班 163 163 165 165 165 166 166 167
三班 163 164 164 164 165 166 167 167
四、典型例题
s九2=
s三2=
s九2<s三2
九班 163 163 165 165 165 166 166 167
三班 163 164 164 164 165 166 167 167
九
三
所以九班啦啦操队女同学的身高更整齐.
四、典型例题
方法二:
九班 163 163 165 165 165 166 166 167
三班 163 164 164 164 165 166 167 167
取 a = 165,得到九班和三班的新数据如下表所示:
九班 -2 -2 0 0 0 1 1 2
三班 -2 -1 -1 -1 0 1 2 2
九
三
s九2=
s三2=
s九2<s三2
四、典型例题
求一组较大数据的方差,有如下简便计算方法:
四、典型例题
归纳总结
(1)任取一个基准数a
(2)将原数据减去a,得到一组新数据
(3)求新数据的方差
【当堂检测】
分析:根据方差的意义,反映一组数据的波动大小,方差越大,波动性越大.
∵S 甲=24,S 乙=18,∴S 甲>S 乙,
∴乙班成绩较为稳定.
B
1.人数相同的八年级(1)、(2)两班学生在同一次数学单元测试中,班级平均分和方差如下: = =80,S 甲=24,S 乙=18,则成绩较为稳定的班级是( )
A.甲班 B.乙班 C.两班成绩一样稳定 D.无法确定
甲
乙
2.甲、乙两名同学进行射击训练,在相同条件下各射靶5次,成绩统计如下:
若从甲、乙两人射击成绩方差的角度评价两人的射击水平,则 同学(填“甲”或“乙”)的射击成绩更稳定些.
命中环数 7 8 9 10
甲命中相应环数的次数 2 2 0 1
乙命中相应环数的次数 1 3 1 0
乙
【当堂检测】
【当堂检测】
3.甲、乙两台编织机纺织一种毛衣,在5天中两台编织机每天出的合格品数如下(单位:件):
甲:7 10 8 8 7 ;乙:8 9 7 9 7 .
计算在这5天中,哪台编织机出合格品的波动较小?
解:
=(7+10+8+8+7)÷5=8,
甲
=(8+9+7+9+7)÷5=8,
乙
S 甲>S 乙,乙台编织机出合格品的波动较小.
甲
乙
四、课堂总结
方差
数据在平均数附近波动比较大时(数据分布比较分散),各个数据与平均数的差的平方和较大,即方差就较大;
数据在平均数附近波动比较小时(数据分布比较集中),各个数据与平均数的差的平方和较小,即方差就较小;
