20.2 数据的波动程度 第2课时 课件 (共16张PPT)2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 20.2 数据的波动程度 第2课时 课件 (共16张PPT)2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 191.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 12:02:54 | ||
图片预览






文档简介
(共16张PPT)
第二十章 数据的分析
20.2 数据的波动程度
第2课时
1.能够用样本方差估计总体的方差
2.会利用样本方差估计总体方差解决简单的实际问题,作出决策
一、学习目标
二、新课导入
问题引入
为了选拔一名同学参加某市中学生射击竞赛,某校对甲、乙两名同学的射击水平进行了测试,两人在相同条件下各射靶10次.
甲成绩(环数) 7 7 6 8 6 5 9 10 7 5
乙成绩(环数) 9 5 7 8 7 6 8 6 7 7
甲
乙
中位数
众数
7
7
7
7
思考:我们应选甲还是乙参加竞赛?
根据方差做决策
三、概念剖析
问题:某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下:
经过计算,甲进球的平均数为 甲=8,方差为S 甲=3.2 .
队员 每人每天进球数
甲 10 6 10 6 8
乙 7 9 7 8 9
(1)求乙进球的平均数和方差;
三、概念剖析
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
解:(1)乙进球的平均数为 乙=
方差为S 乙=
(2)应该选乙队员去参加3分球投篮大赛.
∵S 甲=3.2,S 乙=0.8,
∴S 甲>S 乙,由此说明乙队员更稳定.
三、概念剖析
一般地,在平均数相同的情况下,方差越大,则意味着这组数据对平均数的离散程度也越大.
运用方差解决实际问题的一般步骤:
先计算样本数据平均数,当两组数据的平均数相等或相近时,再利用样本方差来估计总体数据的波动情况.
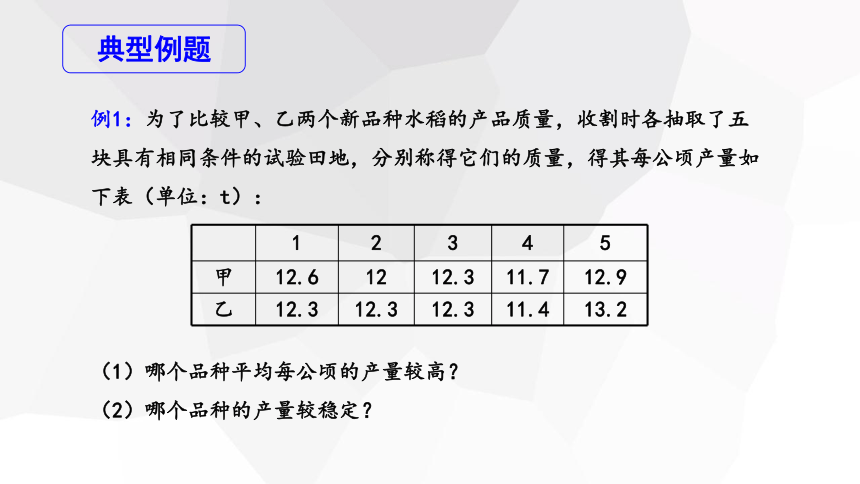
例1:为了比较甲、乙两个新品种水稻的产品质量,收割时各抽取了五块具有相同条件的试验田地,分别称得它们的质量,得其每公顷产量如下表(单位:t):
典型例题
1 2 3 4 5
甲 12.6 12 12.3 11.7 12.9
乙 12.3 12.3 12.3 11.4 13.2
(1)哪个品种平均每公顷的产量较高?
(2)哪个品种的产量较稳定?
(1)哪个品种平均每公顷的产量较高?
典型例题
1 2 3 4 5
甲 12.6 12 12.3 11.7 12.9
乙 12.3 12.3 12.3 11.4 13.2
甲
乙
说明甲、乙两个新品种平均每公顷的产量一样高.
(2)哪个品种的产量较稳定?
典型例题
1 2 3 4 5
甲 12.6 12 12.3 11.7 12.9
乙 12.3 12.3 12.3 11.4 13.2
S 甲
S 乙
∵S 甲<S 乙,
∴甲品种的的产量较稳定.
归纳:
方差越大,数据的波动越大;方差越小,数据的波动越小,可用样本方差估计总体方差.
在解决实际问题时,方差的作用:
反映数据的波动大小.
典型例题
【当堂检测】
1.甲、乙两战士在射击训练中,打靶的次数相同,且打中环数的平均数也相同,如果甲的成绩比乙的成绩稳定,那么方差的大小关系是S 甲 S 乙.
分析:乙根据方差的意义知,甲的成绩稳定,则方差较小,即S 甲<S 乙.
<
【当堂检测】
解:样本数据的平均数分别是
2.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如下表所示.根据表中的数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73
乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75
甲
乙
样本平均数相同,
估计这批鸡腿的平均
质量相近.
【当堂检测】
样本数据的方差分别是
甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73
乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75
S 甲
S 乙
甲
由 = 可知,两家加工厂的鸡腿质量大致相等;
乙
由S 甲<S 乙可知,甲加工厂的鸡腿质量更稳定,大小更均匀.
因此,快餐公司应该选购甲加工厂生产的鸡腿.
【当堂检测】
3.某跳远队准备从甲、乙两名运动员中选取成绩稳定的一名参加比赛.下表是这两名运动员10次测验成绩(单位:m):
你认为应该选择哪名运动员参赛?为什么?
甲 5.85 5.93 6.07 5.91 5.99
6.13 5.98 6.05 6.00 6.19
乙 6.11 6.08 5.83 5.92 5.84
5.81 6.18 6.17 5.85 6.21
【当堂检测】
方差分别是
解:甲、乙测验成绩的平均数分别是
甲
乙
由上可得,S 甲<S 乙,
因此,甲成绩较稳定,应该选甲参加比赛.
S 甲
S 乙
四、课堂总结
1.用样本方差估计总体方差
作用:比较数据的稳定性
2.根据方差做决策,选出最佳方案
方法:先计算样本平均数,再计算样本方差,最后根据方差大小比较离散程度.
第二十章 数据的分析
20.2 数据的波动程度
第2课时
1.能够用样本方差估计总体的方差
2.会利用样本方差估计总体方差解决简单的实际问题,作出决策
一、学习目标
二、新课导入
问题引入
为了选拔一名同学参加某市中学生射击竞赛,某校对甲、乙两名同学的射击水平进行了测试,两人在相同条件下各射靶10次.
甲成绩(环数) 7 7 6 8 6 5 9 10 7 5
乙成绩(环数) 9 5 7 8 7 6 8 6 7 7
甲
乙
中位数
众数
7
7
7
7
思考:我们应选甲还是乙参加竞赛?
根据方差做决策
三、概念剖析
问题:某篮球队对运动员进行3分球投篮成绩测试,每人每天投3分球10次,对甲、乙两名队员在五天中进球的个数统计结果如下:
经过计算,甲进球的平均数为 甲=8,方差为S 甲=3.2 .
队员 每人每天进球数
甲 10 6 10 6 8
乙 7 9 7 8 9
(1)求乙进球的平均数和方差;
三、概念剖析
(2)现在需要根据以上结果,从甲、乙两名队员中选出一人去参加3分球投篮大赛,你认为应该选哪名队员去?为什么?
解:(1)乙进球的平均数为 乙=
方差为S 乙=
(2)应该选乙队员去参加3分球投篮大赛.
∵S 甲=3.2,S 乙=0.8,
∴S 甲>S 乙,由此说明乙队员更稳定.
三、概念剖析
一般地,在平均数相同的情况下,方差越大,则意味着这组数据对平均数的离散程度也越大.
运用方差解决实际问题的一般步骤:
先计算样本数据平均数,当两组数据的平均数相等或相近时,再利用样本方差来估计总体数据的波动情况.
例1:为了比较甲、乙两个新品种水稻的产品质量,收割时各抽取了五块具有相同条件的试验田地,分别称得它们的质量,得其每公顷产量如下表(单位:t):
典型例题
1 2 3 4 5
甲 12.6 12 12.3 11.7 12.9
乙 12.3 12.3 12.3 11.4 13.2
(1)哪个品种平均每公顷的产量较高?
(2)哪个品种的产量较稳定?
(1)哪个品种平均每公顷的产量较高?
典型例题
1 2 3 4 5
甲 12.6 12 12.3 11.7 12.9
乙 12.3 12.3 12.3 11.4 13.2
甲
乙
说明甲、乙两个新品种平均每公顷的产量一样高.
(2)哪个品种的产量较稳定?
典型例题
1 2 3 4 5
甲 12.6 12 12.3 11.7 12.9
乙 12.3 12.3 12.3 11.4 13.2
S 甲
S 乙
∵S 甲<S 乙,
∴甲品种的的产量较稳定.
归纳:
方差越大,数据的波动越大;方差越小,数据的波动越小,可用样本方差估计总体方差.
在解决实际问题时,方差的作用:
反映数据的波动大小.
典型例题
【当堂检测】
1.甲、乙两战士在射击训练中,打靶的次数相同,且打中环数的平均数也相同,如果甲的成绩比乙的成绩稳定,那么方差的大小关系是S 甲 S 乙.
分析:乙根据方差的意义知,甲的成绩稳定,则方差较小,即S 甲<S 乙.
<
【当堂检测】
解:样本数据的平均数分别是
2.检查人员从两家的鸡腿中各随机抽取15个,记录它们的质量(单位:g)如下表所示.根据表中的数据,你认为快餐公司应该选购哪家加工厂的鸡腿?
甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73
乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75
甲
乙
样本平均数相同,
估计这批鸡腿的平均
质量相近.
【当堂检测】
样本数据的方差分别是
甲 74 74 75 74 76 73 76 73 76 75 78 77 74 72 73
乙 75 73 79 72 76 71 73 72 78 74 77 78 80 71 75
S 甲
S 乙
甲
由 = 可知,两家加工厂的鸡腿质量大致相等;
乙
由S 甲<S 乙可知,甲加工厂的鸡腿质量更稳定,大小更均匀.
因此,快餐公司应该选购甲加工厂生产的鸡腿.
【当堂检测】
3.某跳远队准备从甲、乙两名运动员中选取成绩稳定的一名参加比赛.下表是这两名运动员10次测验成绩(单位:m):
你认为应该选择哪名运动员参赛?为什么?
甲 5.85 5.93 6.07 5.91 5.99
6.13 5.98 6.05 6.00 6.19
乙 6.11 6.08 5.83 5.92 5.84
5.81 6.18 6.17 5.85 6.21
【当堂检测】
方差分别是
解:甲、乙测验成绩的平均数分别是
甲
乙
由上可得,S 甲<S 乙,
因此,甲成绩较稳定,应该选甲参加比赛.
S 甲
S 乙
四、课堂总结
1.用样本方差估计总体方差
作用:比较数据的稳定性
2.根据方差做决策,选出最佳方案
方法:先计算样本平均数,再计算样本方差,最后根据方差大小比较离散程度.
