第十八章 平行四边形 复习课 课件(共24张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 第十八章 平行四边形 复习课 课件(共24张PPT) 2023-2024学年初中数学人教版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 281.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 12:05:29 | ||
图片预览







文档简介
(共24张PPT)
复习课
第十八章 平行四边形
一、学习目标
1.梳理平行四边形、矩形、菱形、正方形的性质和判定
2.掌握中位线定理和直角三角形的性质定理
3.能解决与四边形相关的几何问题
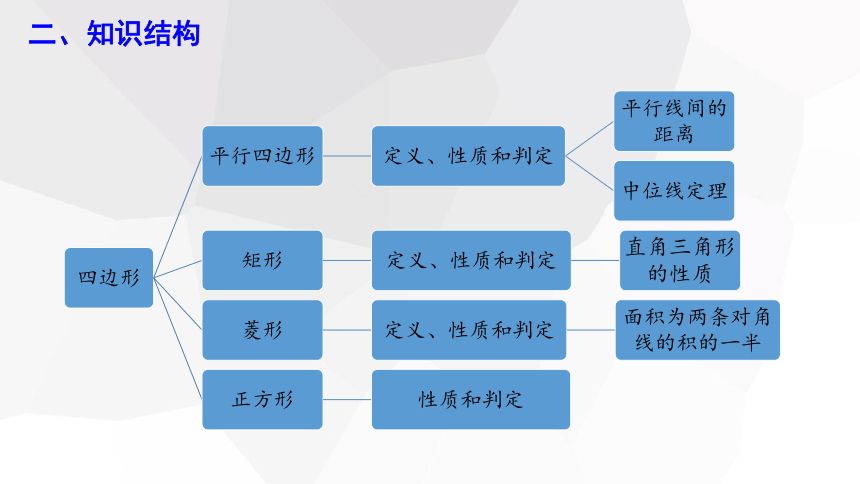
二、知识结构
三、知识梳理
1.平行四边形:
(1)定义:两组对边分别 的四边形叫做平行四边形.
平行
A
B
C
D
O
(2)性质:
b.对角相等;
c.对角线互相平分.
a.对边平行且相等;
(3)判定方法:
a.两组对边分别相等的四边形;
b.两组对角分别相等的四边形;
c.对角线互相平分的四边形;
d.一组对边平行且相等的四边形.
e.两组对边分别平行的四边形.(定义)
三、知识梳理
2.矩形:
(1)定义:有一个角是 的平行四边形叫做矩形.
直角
(2)性质:
b.四个角都是直角;
c.对角线相等.
a.具有平行四边形的所有性质;
(3)判定方法:
a.对角线相等的平行四边形;
b.有三个角是直角的四边形;
c.有一个角是直角的平行四边形.(定义)
B
A
C
D
O
d.是轴对称图形且有2条对称轴.
三、知识梳理
3.菱形:
(1)定义:有一组邻边 的平行四边形叫做菱形.
相等
(2)性质:
b.四条边都相等;
c.两条对角线互相垂直,并且每一条对角线平分一组对角;
a.具有平行四边形的所有性质;
(3)判定方法:
a.对角线互相垂直的平行四边形;
b.四条边相等的四边形;
c.有一组邻边相等的平行四边形.(定义)
C
A
B
D
O
d.是轴对称图形且有2条对称轴.
三、知识梳理
4.正方形:
(1)性质:
b.具有矩形和菱形的特殊性质;
c.是轴对称图形且有4条对称轴.
a.具有平行四边形的所有性质;
(2)判定方法:
a.有一个角是直角的菱形;
b.有一组邻边相等的矩形.
A
B
C
D
O
三、知识梳理
5.平行线间的距离:
定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离;
6.直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
三、知识梳理
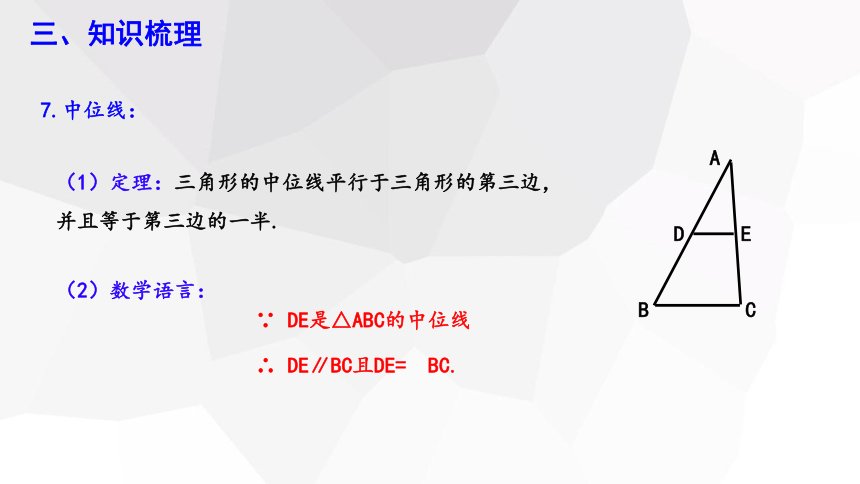
7.中位线:
(1)定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
A
B
C
D
E
∵ DE是△ABC的中位线
(2)数学语言:
∴ DE∥BC且DE= BC.
四、典型例题
(一)平行四边形的性质与判定
例1.如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
证明:在 ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(有一组对边平行且相等的四边形是平行四边形)
∴DF= AD.
又∵CE= BC,
四、典型例题
(一)平行四边形的性质与判定
例1.如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连接DE,CF.
(2)若CD=4,AD=6,∠B=60°,求DE的长.
解:如图,过点D作DH⊥BE于点H.
在 ABCD中,∵∠B=60°,
∴∠DCE=60°,
∵CD=AB=4,
∴在Rt△DHE中,根据勾股定理知DE=
∴CH= CD=2,DH= .
在 CEDF中,CE=DF= AD=3,
H
∴∠CDH=30°.
则EH=CE-CH=3-2=1.
1.如图,在四边形ABCD中,AB=CD,∠BAC=∠DCA.
(1)求证:四边形ABCD为平行四边形.
(2)若AC=4,CD=5,AC⊥BC,求BD的长.
【当堂检测】
(1)证明:∵∠BAC=∠DCA,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD为平行四边形;
(2)∵四边形ABCD为平行四边形,
∴AE=EC=2,BE=DE,AB=CD=5,
∴BC=
∴BE=
∴BD=2BE=
四、典型例题
(二)矩形的性质与判定
例2.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;(有一个角是直角的平行四边形是矩形)
四、典型例题
(二)矩形的性质与判定
例2.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(2)若AD=BE,CF=3,BF=4,求AF的长.
解:∵四边形BFDE是矩形,
∴∠BFD=90°,BE=DF,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5,
∵AD=BE,DF=BE,
∴AD=DF,
∵AD=BC,
∴DF=BE=BC=5,
∵AB=CD=8,
∴AF=
【当堂检测】
2.如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OAB的度数为( )
A.35° B.40° C.45° D.50°
A
四、典型例题
(三)菱形的性质与判定
例3.如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
(1)证明:四边形CFAE为菱形;
证明:∵∠ACB=90°,点E是AB边的中点,
∵点F是点E关于AC所在直线的对称点,
∴AE=AF,CE=CF,
∴CE=EA=AF=CF,
∴四边形CFAE为菱形;(四条边相等的四边形是菱形)
∴CE= AB=EA,
四、典型例题
(三)菱形的性质与判定
例3.如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
(2)连接EF交AC于点O,若BC=10,求线段OF的长.
解:∵四边形CFAE为菱形;
∴OA=OC,OE=OF,
∴OF=5.
∴OE= BC=5,
【当堂检测】
3.如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,则∠AOF= 度.
90
【当堂检测】
4.如图,在菱形ABCD中,∠DAB=60°,点E,F将对角线AC三等分,连接DE,DF,BE,BF.
求证:四边形DEBF为菱形;
证明:如图,连接BD交AC于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OD=OB,
∵AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形.(对角线互相垂直的平行四边形是菱形)
O
四、典型例题
(四)正方形的性质与判定
例4.如图,已知正方形ABCD,P是对角线AC上任意一点,过点P作PM⊥AD于点M,PN⊥AB于点N.
(1)求证:四边形PMAN是正方形;
证明:∵四边形ABCD是正方形,
∴∠BAD=90°,AC平分∠BAD,
∵PM⊥AD,PN⊥AB,
∴∠PMA=∠PNA=90°,
∴四边形PMAN是矩形,
∴四边形PMAN是正方形;(有一组邻边相等的矩形是正方形)
又∵AP=AP,
∴△ANP≌△PMA,
∴PM=PN,
∴∠BAC=∠CAD,
四、典型例题
(四)正方形的性质与判定
例4.如图,已知正方形ABCD,P是对角线AC上任意一点,过点P作PM⊥AD于点M,PN⊥AB于点N.
(2)若E是AM上一点,且∠EPA=15°,求出∠MEP的度数.
解:∵四边形PMAN是正方形,
∴∠APM=45°,∠AMP=90°,
∵∠APE=15°,
∴∠EPM=30°,
∴∠MEP=180°-∠EPM-∠AMP=180°-30°-90°=60°.
【当堂检测】
5.如图,四边形ABCD中,对角线AC,BD相等且互相平分,再添加一个条件,使得四边形ABCD是正方形,可添加的条件是 .(写出一个条件即可)
AB=BC
【当堂检测】
6.如图,正方形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.
求证:四边形OBEC是正方形.
证明:∵BE∥AC,CE∥DB,
∴四边形OBEC是平行四边形,
∵四边形ABCD是正方形,
∴OC=OB,AC⊥BD,
∴∠BOC=90°,
∴四边形OBEC是矩形,
∵OC=OB,
∴四边形OBEC是正方形.
五、课堂总结
四边
形
平行四边形
正方形
菱形
矩形
两组对边分别平行
一组邻边相等
一组邻边相等
一个角是直角
一个角是直角
复习课
第十八章 平行四边形
一、学习目标
1.梳理平行四边形、矩形、菱形、正方形的性质和判定
2.掌握中位线定理和直角三角形的性质定理
3.能解决与四边形相关的几何问题
二、知识结构
三、知识梳理
1.平行四边形:
(1)定义:两组对边分别 的四边形叫做平行四边形.
平行
A
B
C
D
O
(2)性质:
b.对角相等;
c.对角线互相平分.
a.对边平行且相等;
(3)判定方法:
a.两组对边分别相等的四边形;
b.两组对角分别相等的四边形;
c.对角线互相平分的四边形;
d.一组对边平行且相等的四边形.
e.两组对边分别平行的四边形.(定义)
三、知识梳理
2.矩形:
(1)定义:有一个角是 的平行四边形叫做矩形.
直角
(2)性质:
b.四个角都是直角;
c.对角线相等.
a.具有平行四边形的所有性质;
(3)判定方法:
a.对角线相等的平行四边形;
b.有三个角是直角的四边形;
c.有一个角是直角的平行四边形.(定义)
B
A
C
D
O
d.是轴对称图形且有2条对称轴.
三、知识梳理
3.菱形:
(1)定义:有一组邻边 的平行四边形叫做菱形.
相等
(2)性质:
b.四条边都相等;
c.两条对角线互相垂直,并且每一条对角线平分一组对角;
a.具有平行四边形的所有性质;
(3)判定方法:
a.对角线互相垂直的平行四边形;
b.四条边相等的四边形;
c.有一组邻边相等的平行四边形.(定义)
C
A
B
D
O
d.是轴对称图形且有2条对称轴.
三、知识梳理
4.正方形:
(1)性质:
b.具有矩形和菱形的特殊性质;
c.是轴对称图形且有4条对称轴.
a.具有平行四边形的所有性质;
(2)判定方法:
a.有一个角是直角的菱形;
b.有一组邻边相等的矩形.
A
B
C
D
O
三、知识梳理
5.平行线间的距离:
定义:两条平行线中,一条直线上任意一点到另一条直线的距离,叫做这两条平行线之间的距离;
6.直角三角形的一个性质:
直角三角形斜边上的中线等于斜边的一半.
三、知识梳理
7.中位线:
(1)定理:三角形的中位线平行于三角形的第三边,并且等于第三边的一半.
A
B
C
D
E
∵ DE是△ABC的中位线
(2)数学语言:
∴ DE∥BC且DE= BC.
四、典型例题
(一)平行四边形的性质与判定
例1.如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连接DE,CF.
(1)求证:四边形CEDF是平行四边形;
证明:在 ABCD中,AD∥BC,且AD=BC.
∵F是AD的中点,
∴DF=CE,且DF∥CE,
∴四边形CEDF是平行四边形;
(有一组对边平行且相等的四边形是平行四边形)
∴DF= AD.
又∵CE= BC,
四、典型例题
(一)平行四边形的性质与判定
例1.如图,在平行四边形ABCD中,F是AD的中点,延长BC到点E,使CE= BC,连接DE,CF.
(2)若CD=4,AD=6,∠B=60°,求DE的长.
解:如图,过点D作DH⊥BE于点H.
在 ABCD中,∵∠B=60°,
∴∠DCE=60°,
∵CD=AB=4,
∴在Rt△DHE中,根据勾股定理知DE=
∴CH= CD=2,DH= .
在 CEDF中,CE=DF= AD=3,
H
∴∠CDH=30°.
则EH=CE-CH=3-2=1.
1.如图,在四边形ABCD中,AB=CD,∠BAC=∠DCA.
(1)求证:四边形ABCD为平行四边形.
(2)若AC=4,CD=5,AC⊥BC,求BD的长.
【当堂检测】
(1)证明:∵∠BAC=∠DCA,
∴AB∥CD,
又∵AB=CD,
∴四边形ABCD为平行四边形;
(2)∵四边形ABCD为平行四边形,
∴AE=EC=2,BE=DE,AB=CD=5,
∴BC=
∴BE=
∴BD=2BE=
四、典型例题
(二)矩形的性质与判定
例2.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(1)求证:四边形BFDE是矩形;
证明:∵四边形ABCD是平行四边形,
∴AB∥DC,
∵DF=BE,
∴四边形BFDE是平行四边形,
∵DE⊥AB,
∴∠DEB=90°,
∴四边形BFDE是矩形;(有一个角是直角的平行四边形是矩形)
四、典型例题
(二)矩形的性质与判定
例2.如图,在平行四边形ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
(2)若AD=BE,CF=3,BF=4,求AF的长.
解:∵四边形BFDE是矩形,
∴∠BFD=90°,BE=DF,
∴∠BFC=90°,
在Rt△BCF中,CF=3,BF=4,
∴BC=5,
∵AD=BE,DF=BE,
∴AD=DF,
∵AD=BC,
∴DF=BE=BC=5,
∵AB=CD=8,
∴AF=
【当堂检测】
2.如图,在 ABCD中,对角线AC、BD相交于点O,且OA=OD,∠OAD=55°,则∠OAB的度数为( )
A.35° B.40° C.45° D.50°
A
四、典型例题
(三)菱形的性质与判定
例3.如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
(1)证明:四边形CFAE为菱形;
证明:∵∠ACB=90°,点E是AB边的中点,
∵点F是点E关于AC所在直线的对称点,
∴AE=AF,CE=CF,
∴CE=EA=AF=CF,
∴四边形CFAE为菱形;(四条边相等的四边形是菱形)
∴CE= AB=EA,
四、典型例题
(三)菱形的性质与判定
例3.如图,在四边形ABCF中,∠ACB=90°,点E是AB边的中点,点F恰是点E关于AC所在直线的对称点.
(2)连接EF交AC于点O,若BC=10,求线段OF的长.
解:∵四边形CFAE为菱形;
∴OA=OC,OE=OF,
∴OF=5.
∴OE= BC=5,
【当堂检测】
3.如图,AD是△ABC的角平分线,DE∥AC交AB于E,DF∥AB交AC于F.且AD交EF于O,则∠AOF= 度.
90
【当堂检测】
4.如图,在菱形ABCD中,∠DAB=60°,点E,F将对角线AC三等分,连接DE,DF,BE,BF.
求证:四边形DEBF为菱形;
证明:如图,连接BD交AC于点O.
∵四边形ABCD是菱形,
∴AC⊥BD,OA=OC,OD=OB,
∵AE=CF,
∴OE=OF,
∴四边形DEBF是平行四边形,
∵EF⊥BD,
∴四边形DEBF是菱形.(对角线互相垂直的平行四边形是菱形)
O
四、典型例题
(四)正方形的性质与判定
例4.如图,已知正方形ABCD,P是对角线AC上任意一点,过点P作PM⊥AD于点M,PN⊥AB于点N.
(1)求证:四边形PMAN是正方形;
证明:∵四边形ABCD是正方形,
∴∠BAD=90°,AC平分∠BAD,
∵PM⊥AD,PN⊥AB,
∴∠PMA=∠PNA=90°,
∴四边形PMAN是矩形,
∴四边形PMAN是正方形;(有一组邻边相等的矩形是正方形)
又∵AP=AP,
∴△ANP≌△PMA,
∴PM=PN,
∴∠BAC=∠CAD,
四、典型例题
(四)正方形的性质与判定
例4.如图,已知正方形ABCD,P是对角线AC上任意一点,过点P作PM⊥AD于点M,PN⊥AB于点N.
(2)若E是AM上一点,且∠EPA=15°,求出∠MEP的度数.
解:∵四边形PMAN是正方形,
∴∠APM=45°,∠AMP=90°,
∵∠APE=15°,
∴∠EPM=30°,
∴∠MEP=180°-∠EPM-∠AMP=180°-30°-90°=60°.
【当堂检测】
5.如图,四边形ABCD中,对角线AC,BD相等且互相平分,再添加一个条件,使得四边形ABCD是正方形,可添加的条件是 .(写出一个条件即可)
AB=BC
【当堂检测】
6.如图,正方形ABCD的对角线AC、BD相交于点O,BE∥AC,CE∥DB.
求证:四边形OBEC是正方形.
证明:∵BE∥AC,CE∥DB,
∴四边形OBEC是平行四边形,
∵四边形ABCD是正方形,
∴OC=OB,AC⊥BD,
∴∠BOC=90°,
∴四边形OBEC是矩形,
∵OC=OB,
∴四边形OBEC是正方形.
五、课堂总结
四边
形
平行四边形
正方形
菱形
矩形
两组对边分别平行
一组邻边相等
一组邻边相等
一个角是直角
一个角是直角
