第十七章 勾股定理 复习课 课件(共20张PPT) 2023-2024学年初中数学人教版八年级下册
文档属性
| 名称 | 第十七章 勾股定理 复习课 课件(共20张PPT) 2023-2024学年初中数学人教版八年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 268.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 12:07:58 | ||
图片预览





文档简介
(共20张PPT)
复习课
第十七章 勾股定理
一、学习目标
1.能掌握勾股定理,会应用勾股定理求得第三边的长
2.能运用勾股定理的逆定理,判断一个三角形是否为直角三角形
3.能理解互逆命题与互逆定理之间的关系,能区分勾股定理及其逆定理应用的前提条件
4.能运用勾股定理及其逆定理解决实际问题,体会数学建模和转化思想,感受数学的实用性
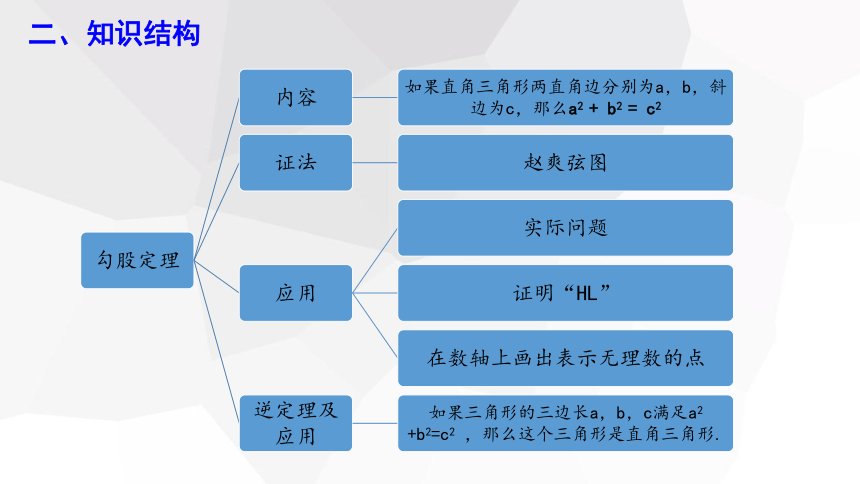
二、知识结构
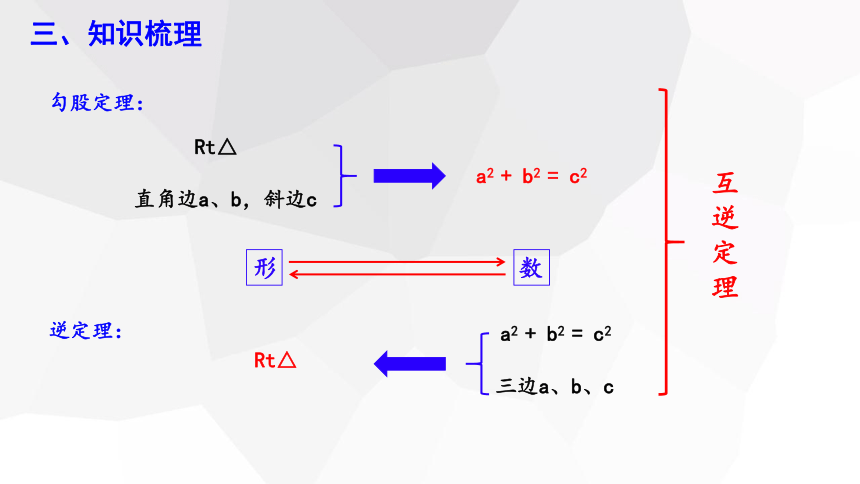
三、知识梳理
1.勾股定理:
如果直角三角形两直角边分别为a,b,斜边为c,那么 .
a2 + b2 = c2
2.勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是 .
直角三角形
三、知识梳理
Rt△
直角边a、b,斜边c
a2 + b2 = c2
勾股定理:
逆定理:
a2 + b2 = c2
三边a、b、c
Rt△
数
形
互逆定理
三、知识梳理
3.原命题、逆命题和逆定理:
(1)如果两个命题的题设和结论正好 ,那么这样的两个命题叫做
命题.如果把其中一个叫做原命题,那么另一个叫做它的 .
相反
互逆
逆命题
(2)如果一个定理的逆命题经过证明是 ,那么它也是一个定理,我们称这两个定理互为逆定理.
正确
4.勾股数:
直角三角形三条边长都是 ,称这三个数为勾股数.
正整数
四、典型例题
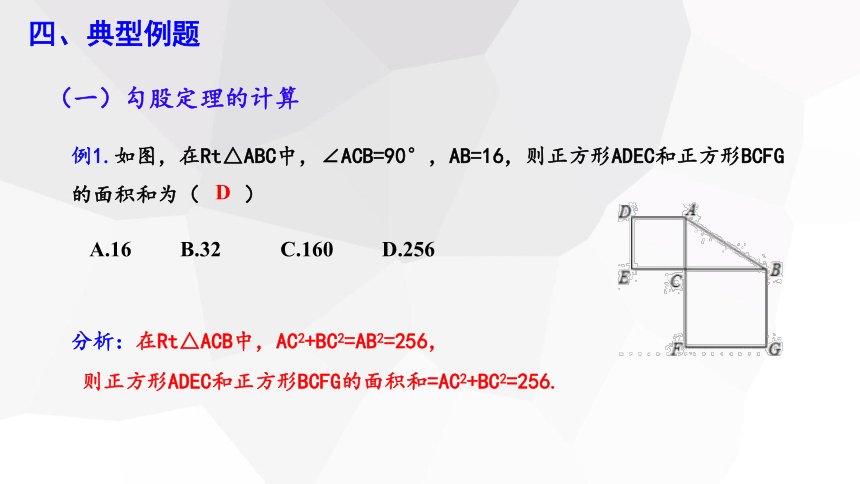
例1.如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )
(一)勾股定理的计算
A.16 B.32 C.160 D.256
分析:在Rt△ACB中,AC2+BC2=AB2=256,
D
则正方形ADEC和正方形BCFG的面积和=AC2+BC2=256.
1.某直角三角形的一直角边长为8,另一直角边长与斜边长的和为32,则斜边的长为( )
A. 8 B. 10 C. 15 D. 17
分析:设直角三角形的斜边长为x,
D
【当堂检测】
由勾股定理得,x2=82+(32-x)2,
解得,x=17.
【当堂检测】
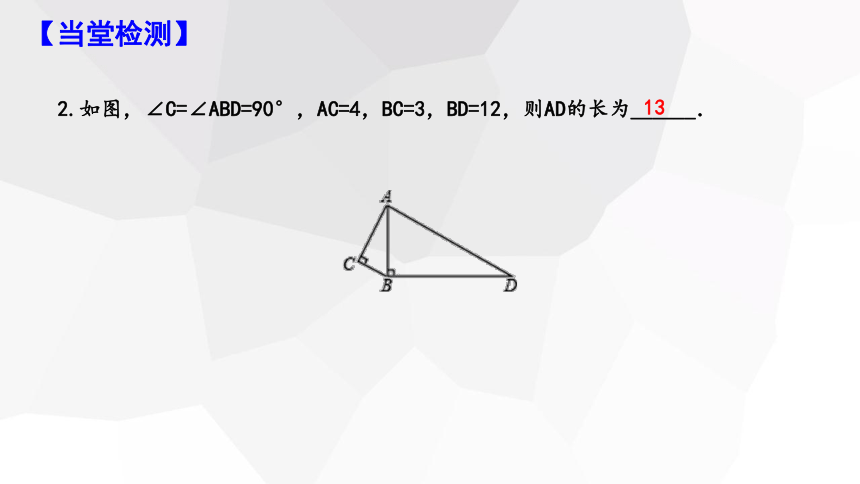
2.如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD的长为______.
13
四、典型例题
(二)运用勾股定理解决问题
例2.在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
解:如图,过C作CD⊥AB于D.
D
四、典型例题
因为BC=400米,AC=300米,∠ACB=90°,
所以根据勾股定理有AB2=AC2+BC2=5002.
因为S△ABC= AB CD= BC AC
所以CD= = =240(米).
由于240米<250米,故有危险,
因此AB段公路需要暂时封锁.
【当堂检测】
3.为修建高速铁路需凿通隧道AC,测得∠BAC=50°,∠B=40°,AB=15km,BC=12km,若每天可凿隧道0.3km,需要几天才能把隧道AC凿通?
解:∵∠A=50°,∠B=40°,
∴∠C=90°.
∵AB=15km,BC=12km,
∴AC2=AB2 BC2=152 122=92
∴ =30(天)
答:需要30天才能将隧道凿通.
四、典型例题
(三)勾股定理的逆定理
例3.如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
解:如图,连接BE.
因为AE2=12+32=10,AB2=12+32=10,
BE2=22+42=20,所以AE2+AB2=BE2.
所以△ABE是直角三角形,且∠BAE=90°,
即AB⊥AE.
【当堂检测】
4.有下面的判断:
①若△ABC中,a2+b2≠c2,则△ABC不是直角三角形;
②△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若△ABC中,a2-b2=c2,则△ABC是直角三角形;
④若△ABC是直角三角形,则(a+b)(a-b)=c2.
其中判断一定正确的有___________.
② ③
【当堂检测】
5.已知下列图形中的三角形的顶点都在正方形的格点上,可以判定三角形是直角三角形的有________.
(2)(4)
四、典型例题
(四)勾股定理与勾股定理的逆定理的综合应用
例4.如图,在△ABC中,D是BC边上一点,已知AB=13,AD=12,AC=15,BD=5,求CD的长.
解:在△ABD中,由52+122=132,可知
AD2+BD2=AB2.
由勾股定理的逆定理知∠ADB=90°.
从而∠ADC=90°.
在Rt△ADC中,由CD2=AC2-AD2,得
因此CD的长为9.
四、典型例题
方法归纳总结:
(1)利用勾股定理的逆定理可解决下列问题:
①判断三角形的形状;②求角的度数、三角形的边长及面积等;③证明垂直关系.
(2)勾股定理是将“形”转化为“数”,勾股定理的逆定理是将“数”转化为“形”.
【当堂检测】
6.如图,已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=6m,AD=8m,BC=24cm,AB=26m,
若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
【当堂检测】
解:连接AC,
在Rt△ACD中,AC2=CD2+AD2=62+82=102,
在△ABC中,AB2=262,BC2=242,
而102+242=262,即AC2+BC2=AB2,
∴∠ACB=90°,
S四边形ABCD=S△ACB-S△ACD= AC BC﹣ AD CD,
所以需费用96×200=19200(元).
= ×10×24﹣ ×8×6
= 96.
五、课堂总结
勾股定理
直角三角形边
长的数量关系
勾股定理
的逆定理
直角三角
形的判定
互逆定理
复习课
第十七章 勾股定理
一、学习目标
1.能掌握勾股定理,会应用勾股定理求得第三边的长
2.能运用勾股定理的逆定理,判断一个三角形是否为直角三角形
3.能理解互逆命题与互逆定理之间的关系,能区分勾股定理及其逆定理应用的前提条件
4.能运用勾股定理及其逆定理解决实际问题,体会数学建模和转化思想,感受数学的实用性
二、知识结构
三、知识梳理
1.勾股定理:
如果直角三角形两直角边分别为a,b,斜边为c,那么 .
a2 + b2 = c2
2.勾股定理的逆定理:
如果三角形的三边长a,b,c满足a2 +b2=c2 ,那么这个三角形是 .
直角三角形
三、知识梳理
Rt△
直角边a、b,斜边c
a2 + b2 = c2
勾股定理:
逆定理:
a2 + b2 = c2
三边a、b、c
Rt△
数
形
互逆定理
三、知识梳理
3.原命题、逆命题和逆定理:
(1)如果两个命题的题设和结论正好 ,那么这样的两个命题叫做
命题.如果把其中一个叫做原命题,那么另一个叫做它的 .
相反
互逆
逆命题
(2)如果一个定理的逆命题经过证明是 ,那么它也是一个定理,我们称这两个定理互为逆定理.
正确
4.勾股数:
直角三角形三条边长都是 ,称这三个数为勾股数.
正整数
四、典型例题
例1.如图,在Rt△ABC中,∠ACB=90°,AB=16,则正方形ADEC和正方形BCFG的面积和为( )
(一)勾股定理的计算
A.16 B.32 C.160 D.256
分析:在Rt△ACB中,AC2+BC2=AB2=256,
D
则正方形ADEC和正方形BCFG的面积和=AC2+BC2=256.
1.某直角三角形的一直角边长为8,另一直角边长与斜边长的和为32,则斜边的长为( )
A. 8 B. 10 C. 15 D. 17
分析:设直角三角形的斜边长为x,
D
【当堂检测】
由勾股定理得,x2=82+(32-x)2,
解得,x=17.
【当堂检测】
2.如图,∠C=∠ABD=90°,AC=4,BC=3,BD=12,则AD的长为______.
13
四、典型例题
(二)运用勾股定理解决问题
例2.在甲村至乙村间有一条公路,在C处需要爆破,已知点C与公路上的停靠站A的距离为300米,与公路上的另一停靠站B的距离为400米,且CA⊥CB,如图所示,为了安全起见,爆破点C周围半径250米范围内不得进入,问:在进行爆破时,公路AB段是否有危险?是否需要暂时封锁?请用你学过的知识加以解答.
解:如图,过C作CD⊥AB于D.
D
四、典型例题
因为BC=400米,AC=300米,∠ACB=90°,
所以根据勾股定理有AB2=AC2+BC2=5002.
因为S△ABC= AB CD= BC AC
所以CD= = =240(米).
由于240米<250米,故有危险,
因此AB段公路需要暂时封锁.
【当堂检测】
3.为修建高速铁路需凿通隧道AC,测得∠BAC=50°,∠B=40°,AB=15km,BC=12km,若每天可凿隧道0.3km,需要几天才能把隧道AC凿通?
解:∵∠A=50°,∠B=40°,
∴∠C=90°.
∵AB=15km,BC=12km,
∴AC2=AB2 BC2=152 122=92
∴ =30(天)
答:需要30天才能将隧道凿通.
四、典型例题
(三)勾股定理的逆定理
例3.如图,在4×4的正方形网格中,每个小正方形的边长都是1.线段AB,AE分别是图中两个1×3的长方形的对角线,请你说明:AB⊥AE.
解:如图,连接BE.
因为AE2=12+32=10,AB2=12+32=10,
BE2=22+42=20,所以AE2+AB2=BE2.
所以△ABE是直角三角形,且∠BAE=90°,
即AB⊥AE.
【当堂检测】
4.有下面的判断:
①若△ABC中,a2+b2≠c2,则△ABC不是直角三角形;
②△ABC是直角三角形,∠C=90°,则a2+b2=c2;
③若△ABC中,a2-b2=c2,则△ABC是直角三角形;
④若△ABC是直角三角形,则(a+b)(a-b)=c2.
其中判断一定正确的有___________.
② ③
【当堂检测】
5.已知下列图形中的三角形的顶点都在正方形的格点上,可以判定三角形是直角三角形的有________.
(2)(4)
四、典型例题
(四)勾股定理与勾股定理的逆定理的综合应用
例4.如图,在△ABC中,D是BC边上一点,已知AB=13,AD=12,AC=15,BD=5,求CD的长.
解:在△ABD中,由52+122=132,可知
AD2+BD2=AB2.
由勾股定理的逆定理知∠ADB=90°.
从而∠ADC=90°.
在Rt△ADC中,由CD2=AC2-AD2,得
因此CD的长为9.
四、典型例题
方法归纳总结:
(1)利用勾股定理的逆定理可解决下列问题:
①判断三角形的形状;②求角的度数、三角形的边长及面积等;③证明垂直关系.
(2)勾股定理是将“形”转化为“数”,勾股定理的逆定理是将“数”转化为“形”.
【当堂检测】
6.如图,已知某开发区有一块四边形空地ABCD,现计划在该空地上种植草皮,经测量∠ADC=90°,CD=6m,AD=8m,BC=24cm,AB=26m,
若每平方米草皮需200元,则在该空地上种植草皮共需多少钱?
【当堂检测】
解:连接AC,
在Rt△ACD中,AC2=CD2+AD2=62+82=102,
在△ABC中,AB2=262,BC2=242,
而102+242=262,即AC2+BC2=AB2,
∴∠ACB=90°,
S四边形ABCD=S△ACB-S△ACD= AC BC﹣ AD CD,
所以需费用96×200=19200(元).
= ×10×24﹣ ×8×6
= 96.
五、课堂总结
勾股定理
直角三角形边
长的数量关系
勾股定理
的逆定理
直角三角
形的判定
互逆定理
