浙教版2023-2024学年浙江省杭州市八年级(下)开学考试模拟数学卷(含解析)
文档属性
| 名称 | 浙教版2023-2024学年浙江省杭州市八年级(下)开学考试模拟数学卷(含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 813.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2023-2024学年浙江省杭州市八年级(下)开学考试模拟卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列学校的校徽图案是轴对称图形的是( )
A. B.
C. D.
2.y减去2的差不大于0,用不等式表示为( )
A.y﹣2≤0 B.y﹣2≥0 C.y﹣2<0 D.y﹣2>0
3.已知三角形的两边长分别为5cm和7cm,则第三边的长可以是( )
A.1cm B.2cm C.6cm D.12cm
4.直线y=﹣x+3与x轴的交点坐标是( )
A.(0,3) B.(0,﹣3) C.(3,0) D.(﹣3,0)
5.下列命题中是真命题的是( )
A.等边三角形一条边上的高线也是该条边上的中线
B.有一个角是60°的三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.有一个角对应相等的两个等腰三角形全等
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠B=∠D=90° D.∠BCA=∠DCA
7.点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是( )
A.(4,﹣3) B.(4,3) C.(3,﹣4) D.(﹣3,4)
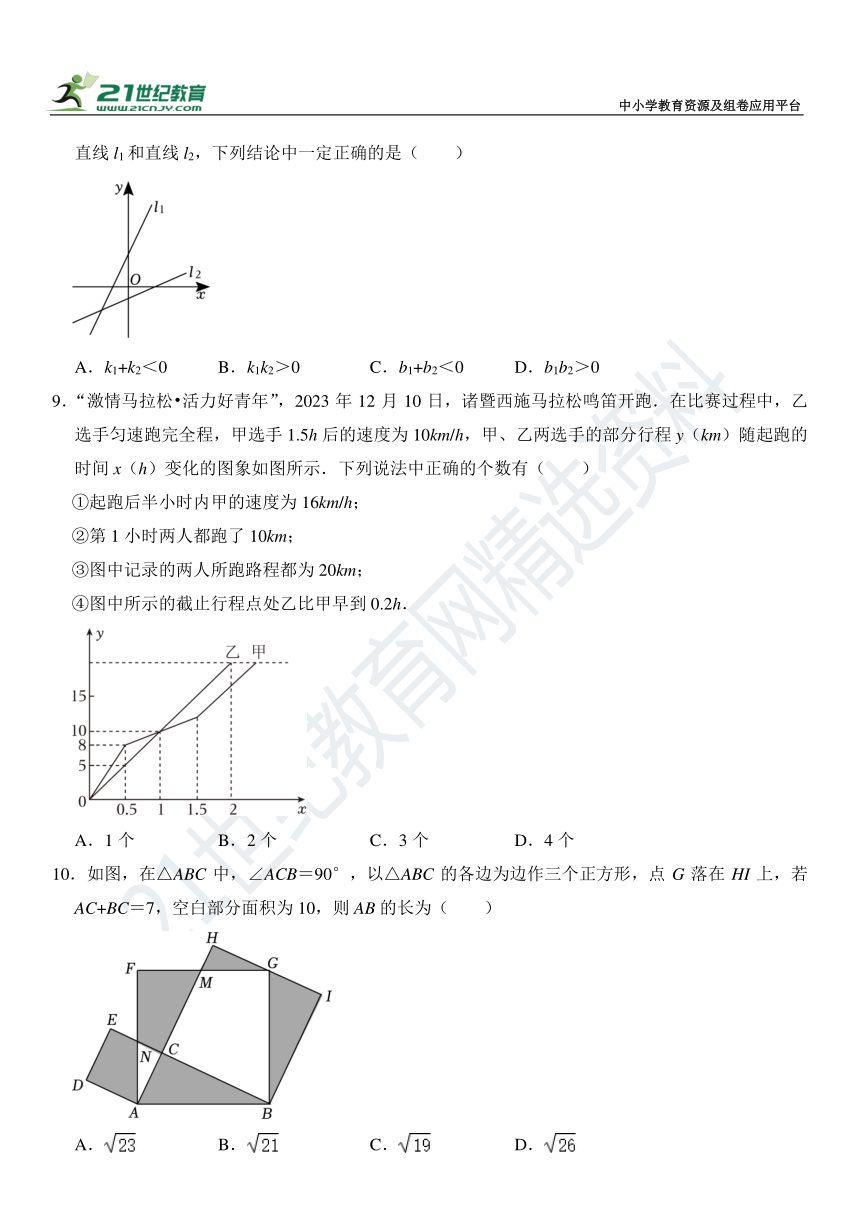
8.如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2(其中k1k2≠0)的图象分别为直线l1和直线l2,下列结论中一定正确的是( )
A.k1+k2<0 B.k1k2>0 C.b1+b2<0 D.b1b2>0
9.“激情马拉松 活力好青年”,2023年12月10日,诸暨西施马拉松鸣笛开跑.在比赛过程中,乙选手匀速跑完全程,甲选手1.5h后的速度为10km/h,甲、乙两选手的部分行程y(km)随起跑的时间x(h)变化的图象如图所示.下列说法中正确的个数有( )
①起跑后半小时内甲的速度为16km/h;
②第1小时两人都跑了10km;
③图中记录的两人所跑路程都为20km;
④图中所示的截止行程点处乙比甲早到0.2h.
A.1个 B.2个 C.3个 D.4个
10.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=7,空白部分面积为10,则AB的长为( )
A. B. C. D.
二.填空题(共6小题,满分24分,每小题4分)
11.在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 .
12.函数的自变量x的取值范围是 .
13.将“对顶角相等”改写为“如果…那么…”的形式,可写为 .
14.将直线y=2x向上平移5个单位后,所得直线对应的函数表达式是 .
15.若关于x的不等式组只有一个整数解,则实数a的取值范围是 .
16.勾股定理的证明方法多样,如图是“水车翼轮法”证明勾股定理:将正方形ACFG沿分割线JK,LM分割成四个全等四边形,再将这四个四边形和正方形ABED拼成大正方形BCHI.若AB=2,,则AL的长为 .
三.解答题(共8小题,满分66分)
17.(6分)在方格纸中,点P、Q都在格点上,请用无刻度的直尺按要求画格点三角形:
(1)在图1中,画一个以PQ为腰的等腰△APQ(A为格点);
(2)在图2中,画一个以PQ为底的等腰△BPQ(B为格点).
18.(6分)解不等式(组):
(1)3x+1≥﹣5;
(2).
19.(6分)如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.
(1)若∠B=60°,∠C=40°,求∠DAE的度数.
(2)若∠B=α,∠C=β(α>β),请直接写出∠DAE的度数(用含α,β的代数式表示).
20.(8分)已知A(﹣3,0),B(5,0),C(x,y).
(1)若点C在第二象限内,且|x|=3,|y|=3,求点C的坐标,并求△ABC的面积;
(2)若点C在第四象限内,且△ABC的面积为8,|x|=4,求点C的坐标.
21.(8分)已知:如图,在△ABC中,AB=2AC,过点C作CD⊥AC,交∠BAC的平分线于点D.求证:∠BAC=2∠ABD.
22.(10分)随着梦天实验舱的顺利发射,我国空间站完成了在轨组装,为了庆祝这令人激动的时刻,某校开展了关于空间站的科学知识问答竞赛.为了奖励在竞赛中表现优异的学生,学校准备一次性购买A,B两种航天器模型作为奖品.已知购买1个A模型和1个B模型共需159元;购买3个A模型和2个B模型共需374元.
(1)求A模型和B模型的单价;
(2)根据学校的实际情况,需一次性购买A模型和B模型共20个,但要求购买A模型的数量多于12个,且不超过B模型的3倍.请你给出一种费用最少的方案,并求出该方案所需的费用.
23.(10分)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x轴交于点A(﹣2,0),与y轴交于点B,且与正比例函数的图象交于点C(m,3).
(1)求m的值和一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且S△PBC=2S△OBC,求点P的坐标.
24.(12分)在四边形ABCD中,AB=BC=CD,∠BCD=60°,∠ABC=α(60°<α<180°),E为AD中点,连接AC,BE交于点F.
(1)当α=100°时,∠BAC= ,∠ABF= ;
(2)当α的大小改变时,∠BFC的度数是否发生改变?若变化,求∠BFC的变化范围,若不变,求∠BFC的度数;
(3)猜想AF,BF,CF之间的数量关系,并说明理由;
(4)若S△ABF:S△CBF=3:8,则= .
2023-2024学年浙江省杭州市八年级(下)开学考试模拟卷
解析卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列学校的校徽图案是轴对称图形的是( )
A. B.
C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:A,C,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
2.y减去2的差不大于0,用不等式表示为( )
A.y﹣2≤0 B.y﹣2≥0 C.y﹣2<0 D.y﹣2>0
【分析】根据“y减去2的差不大于0”,即可列出关于y的一元一次不等式,此题得解.
【解答】解:根据题意得:y﹣2≤0.
故选:A.
3.已知三角形的两边长分别为5cm和7cm,则第三边的长可以是( )
A.1cm B.2cm C.6cm D.12cm
【分析】设三角形第三边的长是x,由三角形三边关系定理得到2<x<12,即可得到答案.
【解答】解:设三角形第三边的长是x,
∴7﹣5<x<7+5,
∴2<x<12,
∴第三边的长可以6cm.
故选:C.
4.直线y=﹣x+3与x轴的交点坐标是( )
A.(0,3) B.(0,﹣3) C.(3,0) D.(﹣3,0)
【分析】令一次函数的解析式中y=0求出x的值,即可得到直线y=﹣x+3与x轴的交点坐标.
【解答】解:令直线y=﹣x+3中y=0,则﹣x+3=0,
解得x=3,
∴直线y=﹣x+3与x轴的交点坐标为(3,0).
故选:C.
5.下列命题中是真命题的是( )
A.等边三角形一条边上的高线也是该条边上的中线
B.有一个角是60°的三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.有一个角对应相等的两个等腰三角形全等
【分析】由等腰三角形的性质,等边三角形的性质,全等三角形的判定,即可判断.
【解答】解:A、等边三角形一条边上的高线也是该条边上的中线,正确,故A符合题意;
B、有一个角是60°的等腰三角形是等边三角形,故B不符合题意;
C、等腰三角形可能的锐角三角形,直角三角形,钝角三角形,故C不符合题意;
D、有一个角对应相等的两个等腰三角形不一定全等,故D不符合题意.
故选:A.
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠B=∠D=90° D.∠BCA=∠DCA
【分析】要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.
【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故C选项不符合题意;
D、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故D选项符合题意;
故选:D.
7.点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是( )
A.(4,﹣3) B.(4,3) C.(3,﹣4) D.(﹣3,4)
【分析】根据第四象限的点的坐标特征,以及点到y轴的距离等于横坐标的绝对值,到x轴的距离等于纵坐标的绝对值,求出点M的横坐标与纵坐标即可得解.
【解答】解:∵点M在第四象限,且点M到x轴的距离为3,到y轴的距离为4,
∴点M的横坐标为4,纵坐标为﹣3,
∴点M的坐标为(4,﹣3).
故选:A.
8.如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2(其中k1k2≠0)的图象分别为直线l1和直线l2,下列结论中一定正确的是( )
A.k1+k2<0 B.k1k2>0 C.b1+b2<0 D.b1b2>0
【分析】根据一次函数y=k1x+b1与y=k2x+b2的图象位置,可得k1>0,b1>0,k2>0,b2<0,然后逐一判断即可解答.
【解答】解:∵一次函数y=k1x+b1的图象过第一、二、三象限,
∴k1>0,b1>0,
∵一次函数y=k2x+b2的图象过第一、三、四象限,
∴k2>0,b2<0,且|b1|>|b2|,
∵A、k1+k2<0,
故A不符合题意;
B、k1k2>0,
故B符合题意;
C、b1+b2>0,
故C不符合题意;
D、b1 b2<0,
故D不符合题意;
故选:B.
9.“激情马拉松 活力好青年”,2023年12月10日,诸暨西施马拉松鸣笛开跑.在比赛过程中,乙选手匀速跑完全程,甲选手1.5h后的速度为10km/h,甲、乙两选手的部分行程y(km)随起跑的时间x(h)变化的图象如图所示.下列说法中正确的个数有( )
①起跑后半小时内甲的速度为16km/h;
②第1小时两人都跑了10km;
③图中记录的两人所跑路程都为20km;
④图中所示的截止行程点处乙比甲早到0.2h.
A.1个 B.2个 C.3个 D.4个
【分析】①根据速度=路程÷时间计算即可;
②根据两图象的交点坐标作答即可;
③图中记录的两人所跑路程相等,根据乙的路程=乙的速度×乙的时间计算即可;
④设当x=a时,三个时间段0≤x<0.5、0.5≤x<1.5、1.5≤x≤a的路程之和为20km,列方程并求解,计算a﹣2的值即可.
【解答】解:当0≤x≤0.5时,甲的速度为8÷0.5=16(km/h),
∴①正确;
根据两图象的交点坐标可知,当x=1时,y=10,
∴②正确;
乙的速度为10÷1=10(km/h),当x=2时,乙所跑的路程为10×2=20(km),
∴③正确;
当0.5<x≤1.5时,甲的速度为(10﹣8)÷(1﹣0.5)=4(km/h),
设当x=a时,甲所跑的路程为20km,则8+4×(1.5﹣0.5)+10×(a﹣1.5)=20,解得a=2.3,
2.3﹣2=0.3(h),
∴图中所示的截止行程点处乙比甲早到0.3h,
∴④不正确;
综上,①②③正确,
故选:C.
10.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=7,空白部分面积为10,则AB的长为( )
A. B. C. D.
【分析】由正方形的性质推出AB=AF,∠BAN=∠F=90°,由余角的性质推出∠ABN=∠MAF,由ASA证明△BAN≌△AFM,得到△BAN的面积=△AFM的面积,因此四边形FNCM的面积=△ABC的面积,得到空白部分的面积=正方形ABGF的面积﹣2×△ABC的面积,因此AB2﹣2×AC BC=10①,由完全平方公式得AC2+BC2+2AC BC=49,由勾股定理得到AB2+2AC BC=49②,于是AB2=23,即可求出AB的长.
【解答】解:∵四边形ABGF是正方形,
∴AB=AF,∠BAN=∠F=90°,
∴∠MAF+∠BAC=90°,
∵∠ACB=90°,
∴∠ABN+∠BAC=90°,
∴∠ABN=∠MAF,
∵AB=AF,∠BAN=∠F,
∴△BAN≌△AFM(ASA),
∴△BAN的面积=△AFM的面积,
∴四边形FNCM的面积=△ABC的面积,
∴空白部分的面积=正方形ABGF的面积﹣2×△ABC的面积,
∴AB2﹣2×AC BC=10①,
∵AC+BC=7,
∴(AC+BC)2=72,
∴AC2+BC2+2AC BC=49,
∵AB2=AC2+BC2,
∴AB2+2AC BC=49②,
由①和②得AB2=23,
∴AB=(舍去负值).
故选:A.
二.填空题(共6小题,满分24分,每小题4分)
11.在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 (3,﹣2) .
【分析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答即可.
【解答】解:点(3,2)关于x轴对称的点的坐标为(3,﹣2).
故答案为:(3,﹣2).
12.函数的自变量x的取值范围是 x≠﹣2 .
【分析】根据分式的分母不为0可得x+2≠0,即可得出答案.
【解答】解:由题意得:x+2≠0,
解得:x≠﹣2.
故答案为:x≠﹣2.
13.将“对顶角相等”改写为“如果…那么…”的形式,可写为 如果两个角是对顶角,那么它们相等 .
【分析】命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.
【解答】解:题设为:对顶角,结论为:相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么它们相等;
故答案为:如果两个角是对顶角,那么它们相等.
14.将直线y=2x向上平移5个单位后,所得直线对应的函数表达式是 y=2x+5 .
【分析】根据平移法则上加下减可得出平移后的解析式.
【解答】解:将直线y=2x向上平移5个单位后,所得直线的函数表达式是:y=2x+5.
故答案为:y=2x+5.
15.若关于x的不等式组只有一个整数解,则实数a的取值范围是 0<a≤1 .
【分析】先解出不等式组中每个不等式的解集,再根据关于x的不等式组只有一个整数解,即可得到a的取值范围.
【解答】解:,
解不等式①,得:x≥a,
解不等式②,得:x≤,
∵关于x的不等式组只有一个整数解,
∴0<a≤1,
故答案为:0<a≤1.
16.勾股定理的证明方法多样,如图是“水车翼轮法”证明勾股定理:将正方形ACFG沿分割线JK,LM分割成四个全等四边形,再将这四个四边形和正方形ABED拼成大正方形BCHI.若AB=2,,则AL的长为 .
【分析】根据勾股定理求出AC的长,再根据题意得出OP=AL,NP=GL,得出AG﹣AL=OP+ON,即可推出结果.
【解答】解:如图,
在Rt△ABC中,由勾股定理得,
AC=,
∴AG=AC=5,
∵将正方形ACFG沿分割线JK,LM分割成四个全等四边形,再将这四个四边形和正方形ABED拼成大正方形BCHI.
∴OP=AL,NP=GL,
∴AG﹣AL=OP+ON,
∴5﹣AL=AL+2,
∴AL=,
故答案为:.
三.解答题(共8小题,满分66分)
17.(6分)在方格纸中,点P、Q都在格点上,请用无刻度的直尺按要求画格点三角形:
(1)在图1中,画一个以PQ为腰的等腰△APQ(A为格点);
(2)在图2中,画一个以PQ为底的等腰△BPQ(B为格点).
【分析】(1)根据等腰三角形的定义画出图形;
(2)根据等腰直角三角形的判定画出图形.
【解答】解:(1)如图1中,△ABC即为所求(答案不唯一);
(2)如图2中,△BPQ即为所求(答案不唯一).
18.(6分)解不等式(组):
(1)3x+1≥﹣5;
(2).
【分析】(1)不等式移项、合并同类项,系数化为1即可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:(1)3x+1≥﹣5,
3x≥﹣5﹣1,
3x≥﹣6,
x≥﹣2;
(2),
解不等式①,得,
解不等式②,得x>2,
故不等式组的解集为.
19.(6分)如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.
(1)若∠B=60°,∠C=40°,求∠DAE的度数.
(2)若∠B=α,∠C=β(α>β),请直接写出∠DAE的度数(用含α,β的代数式表示).
【分析】(1)由高线可得∠ADB=90°,再由三角形的内角和可求得∠BAD=30°,∠BAC=80°,利用角平分线的定义可求得∠BAE=40°,从而可求∠DAE的度数;
(2)参照(1)进行求解即可.
【解答】解:(1)∵AD是△ABC的高线,
∴∠ADB=90°,
∵∠B=60°,∠C=40°,
∴∠BAD=180°﹣∠B﹣∠ADB=30°,
∠BAC=180°﹣∠B﹣∠C=80°,
∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=40°,
∴∠DAE=∠BAE﹣∠BAD=10°;
(2)∵AD是△ABC的高线,
∴∠ADB=90°,
∵∠B=α,∠C=β,
∴∠BAD=180°﹣∠B﹣∠ADB=90°﹣α,
∠BAC=180°﹣∠B﹣∠C=180°﹣α﹣β,
∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=90°﹣,
∴∠DAE=∠BAE﹣∠BAD=.
20.(8分)已知A(﹣3,0),B(5,0),C(x,y).
(1)若点C在第二象限内,且|x|=3,|y|=3,求点C的坐标,并求△ABC的面积;
(2)若点C在第四象限内,且△ABC的面积为8,|x|=4,求点C的坐标.
【分析】(1)因为点C在第二象限内,所以x<0,y>0,因为|x|=3,|y|=3,所以x=﹣3,y=3,即点C的坐标为(﹣3,3),再根据点A(﹣3,0),B(5,0)的坐标,即可得出△ABC的面积;
(2)因为△ABC的面积为8,点C在第四象限内,所以×8×(﹣y)=8,得y=﹣2,由|x|=4,得x=4,即可得出点C的坐标.
【解答】解:(1)∵点C在第二象限内,
∴x<0,y>0,
∵|x|=3,|y|=3,
∴x=﹣3,y=3,
∴点C的坐标为(﹣3,3),
∵A(﹣3,0),B(5,0),
∴△ABC的面积=×8×3=12;
(2)∵△ABC的面积为8,点C在第四象限内,
∴×8×(﹣y)=8,
∴y=﹣2,
∵|x|=4,
∴x=4,
∴点C的坐标为(4,﹣2).
21.(8分)已知:如图,在△ABC中,AB=2AC,过点C作CD⊥AC,交∠BAC的平分线于点D.求证:∠BAC=2∠ABD.
【分析】根据角平分线的性质可得DE=DC,再利用三角形全等可得AE=AC,进而得出DE是AB的中垂线,由中垂线的性质和角平分线的定义可得结论.
【解答】解:过点D作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△AED和Rt△ACD中,
∵DE=DC,AD=AD,
∴Rt△AED≌Rt△ACD(HL),
∴AE=AC,
又∵AB=2AC,
∴AE=BE,
∴DE是AB的中垂线,
∴DA=DB,
∴∠ABD=∠BAD,
∵∠BAD=∠CAD=∠BAC,
∴∠ABD=∠BAC,
即∠BAC=2∠ABD.
22.(10分)随着梦天实验舱的顺利发射,我国空间站完成了在轨组装,为了庆祝这令人激动的时刻,某校开展了关于空间站的科学知识问答竞赛.为了奖励在竞赛中表现优异的学生,学校准备一次性购买A,B两种航天器模型作为奖品.已知购买1个A模型和1个B模型共需159元;购买3个A模型和2个B模型共需374元.
(1)求A模型和B模型的单价;
(2)根据学校的实际情况,需一次性购买A模型和B模型共20个,但要求购买A模型的数量多于12个,且不超过B模型的3倍.请你给出一种费用最少的方案,并求出该方案所需的费用.
【分析】(1)设A模型的单价是x元,B模型的单价是y元,根据“购买1个A模型和1个B模型共需159元;购买3个A模型和2个B模型共需374元”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买m个A模型,则购买(20﹣m)个B模型,根据“购买A模型的数量多于12个,且不超过B模型的3倍”,可列出关于m的一元一次不等式组,解之可得出m的取值范围,结合m为正整数,可得出各购买方案,再求出各方案所需费用,比较后即可得出结论.
【解答】解:(1)设A模型的单价是x元,B模型的单价是y元,
根据题意得:,
解得:.
答:A模型的单价是56元,B模型的单价是103元;
(2)设购买m个A模型,则购买(20﹣m)个B模型,
根据题意得:,
解得:12<m≤15,
又∵m为正整数,
∴m的值为13,14,15,
∴该学校共有3种购买方案,
方案1:购买13个A模型,7个B模型,所需费用为56×13+103×7=1449(元);
方案2:购买14个A模型,6个B模型,所需费用为56×14+103×6=1402(元);
方案3:购买15个A模型,5个B模型,所需费用为56×15+103×5=1355(元),
∵1449>1402>1355,
∴购买15个A模型,5个B模型费用最少,该方案所需的费用为1355元.
23.(10分)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x轴交于点A(﹣2,0),与y轴交于点B,且与正比例函数的图象交于点C(m,3).
(1)求m的值和一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且S△PBC=2S△OBC,求点P的坐标.
【分析】(1)将点C(m,3)代入可得m=4,再用待定系数法求一次函数的解析式即可;
(2)由y=x+1可求得B的坐标,即可利用三角形面积求得S△OBC=,根据S△PBC=2S△OBC得到BP 3=3,解得BP=2,进而即可求得P的坐标.
【解答】解:(1)∵将点C(m,3)代入,
∴3=m,
∴m=4,
∴C(4,3),
将A(﹣2,0),C(4,3)代入一次函数的解析式为y=kx+b得:
,
解得,
∴一次函数y=kx+b的表达式为y=x+1;
(2)令x=0,则y=x+1=1,
∴B(0,1),
∴OB=1,
∴S△OBC=OB xC=,
∵S△PBC=2S△OBC,
∴S△BPC=BP xC=3,即BP 3=3,
∴BP=2,
∴点P的坐标为(0,3)或(0,﹣1).
24.(12分)在四边形ABCD中,AB=BC=CD,∠BCD=60°,∠ABC=α(60°<α<180°),E为AD中点,连接AC,BE交于点F.
(1)当α=100°时,∠BAC= 40° ,∠ABF= 20° ;
(2)当α的大小改变时,∠BFC的度数是否发生改变?若变化,求∠BFC的变化范围,若不变,求∠BFC的度数;
(3)猜想AF,BF,CF之间的数量关系,并说明理由;
(4)若S△ABF:S△CBF=3:8,则= .
【分析】(1)根据等腰三角形的性质即可求出∠BAC的度数,根据,可以求出∠ABF的度数;
(2)连接BD,求出△BCD是等边三角形,分别表示出∠ABE,∠BAC,即可求解;
(3)如图,作∠FBG=60°,BG交AC于点G,求出△BFG是等边三角形,再证明△AFB≌△CGB(AAS),从而得出AF,BF,CF之间的数量关系;
(4)根据,设AF=3a,CF=8a,结合(3)得出BF=GF=CF﹣CG=5a,再根据∠CAE=30°,由30度直角三角形性质得出,由此即可解题.
【解答】解:(1)∵AB=BC,∠ABC=α=100°,
∴∠BAC=∠BCA=40°,
如图,连接BD
∵BC=CD,∠BCD=60°,
∴△BCD是等边三角形
∴BD=CD=AD,∠CBD=60°,
又∵E为AD中点,
∴,
∵AB=BC,
∴.
∴.
∵∠BFC=∠BAC+∠ABF,
∴∠ABF=60°﹣40°=20°.
故答案为:40°,20°;
(2)结论:不变,
证明:如图,连接BD,
∵BC=CD,∠BCD=60°,
∴△BCD是等边三角形,
∴BD=CD=AD,∠CBD=60°,
又∵E为AD中点,
∴,
∵AB=BC,
∴.
∴;
(3)如图,作∠FBG=60°,BG交AC于点G.
∵∠BFC=60°,∠FBG=60°,
∴△BFG是等边三角形,
∴∠BGF=60°,BF=FG,
∴∠BGC=∠BFA=120°,
∵AB=BC,
∴∠BAC=∠BCA,
∴△AFB≌△CGB(AAS),
∴AF=GC,
∵CG+CF=CF,AF=GC,BF=FG,
∴AF+BF=CF.
(4)∵,
∴设AF=3a,CF=8a,
由(3)得:AF+BF=CF,
∴BF=CF﹣AF=5a,
∵BA=BD,E为AD中点,
∴BE⊥AD,
由(2)知∠BFC=60°,
∴∠AFE=∠BFC=60°,
∴∠CAE=30°,
在Rt△AFE中,∠CAE=30°,
∴,
∴.
故答案为:.
2023-2024学年浙江省杭州市八年级(下)开学考试模拟卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列学校的校徽图案是轴对称图形的是( )
A. B.
C. D.
2.y减去2的差不大于0,用不等式表示为( )
A.y﹣2≤0 B.y﹣2≥0 C.y﹣2<0 D.y﹣2>0
3.已知三角形的两边长分别为5cm和7cm,则第三边的长可以是( )
A.1cm B.2cm C.6cm D.12cm
4.直线y=﹣x+3与x轴的交点坐标是( )
A.(0,3) B.(0,﹣3) C.(3,0) D.(﹣3,0)
5.下列命题中是真命题的是( )
A.等边三角形一条边上的高线也是该条边上的中线
B.有一个角是60°的三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.有一个角对应相等的两个等腰三角形全等
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠B=∠D=90° D.∠BCA=∠DCA
7.点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是( )
A.(4,﹣3) B.(4,3) C.(3,﹣4) D.(﹣3,4)
8.如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2(其中k1k2≠0)的图象分别为直线l1和直线l2,下列结论中一定正确的是( )
A.k1+k2<0 B.k1k2>0 C.b1+b2<0 D.b1b2>0
9.“激情马拉松 活力好青年”,2023年12月10日,诸暨西施马拉松鸣笛开跑.在比赛过程中,乙选手匀速跑完全程,甲选手1.5h后的速度为10km/h,甲、乙两选手的部分行程y(km)随起跑的时间x(h)变化的图象如图所示.下列说法中正确的个数有( )
①起跑后半小时内甲的速度为16km/h;
②第1小时两人都跑了10km;
③图中记录的两人所跑路程都为20km;
④图中所示的截止行程点处乙比甲早到0.2h.
A.1个 B.2个 C.3个 D.4个
10.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=7,空白部分面积为10,则AB的长为( )
A. B. C. D.
二.填空题(共6小题,满分24分,每小题4分)
11.在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 .
12.函数的自变量x的取值范围是 .
13.将“对顶角相等”改写为“如果…那么…”的形式,可写为 .
14.将直线y=2x向上平移5个单位后,所得直线对应的函数表达式是 .
15.若关于x的不等式组只有一个整数解,则实数a的取值范围是 .
16.勾股定理的证明方法多样,如图是“水车翼轮法”证明勾股定理:将正方形ACFG沿分割线JK,LM分割成四个全等四边形,再将这四个四边形和正方形ABED拼成大正方形BCHI.若AB=2,,则AL的长为 .
三.解答题(共8小题,满分66分)
17.(6分)在方格纸中,点P、Q都在格点上,请用无刻度的直尺按要求画格点三角形:
(1)在图1中,画一个以PQ为腰的等腰△APQ(A为格点);
(2)在图2中,画一个以PQ为底的等腰△BPQ(B为格点).
18.(6分)解不等式(组):
(1)3x+1≥﹣5;
(2).
19.(6分)如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.
(1)若∠B=60°,∠C=40°,求∠DAE的度数.
(2)若∠B=α,∠C=β(α>β),请直接写出∠DAE的度数(用含α,β的代数式表示).
20.(8分)已知A(﹣3,0),B(5,0),C(x,y).
(1)若点C在第二象限内,且|x|=3,|y|=3,求点C的坐标,并求△ABC的面积;
(2)若点C在第四象限内,且△ABC的面积为8,|x|=4,求点C的坐标.
21.(8分)已知:如图,在△ABC中,AB=2AC,过点C作CD⊥AC,交∠BAC的平分线于点D.求证:∠BAC=2∠ABD.
22.(10分)随着梦天实验舱的顺利发射,我国空间站完成了在轨组装,为了庆祝这令人激动的时刻,某校开展了关于空间站的科学知识问答竞赛.为了奖励在竞赛中表现优异的学生,学校准备一次性购买A,B两种航天器模型作为奖品.已知购买1个A模型和1个B模型共需159元;购买3个A模型和2个B模型共需374元.
(1)求A模型和B模型的单价;
(2)根据学校的实际情况,需一次性购买A模型和B模型共20个,但要求购买A模型的数量多于12个,且不超过B模型的3倍.请你给出一种费用最少的方案,并求出该方案所需的费用.
23.(10分)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x轴交于点A(﹣2,0),与y轴交于点B,且与正比例函数的图象交于点C(m,3).
(1)求m的值和一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且S△PBC=2S△OBC,求点P的坐标.
24.(12分)在四边形ABCD中,AB=BC=CD,∠BCD=60°,∠ABC=α(60°<α<180°),E为AD中点,连接AC,BE交于点F.
(1)当α=100°时,∠BAC= ,∠ABF= ;
(2)当α的大小改变时,∠BFC的度数是否发生改变?若变化,求∠BFC的变化范围,若不变,求∠BFC的度数;
(3)猜想AF,BF,CF之间的数量关系,并说明理由;
(4)若S△ABF:S△CBF=3:8,则= .
2023-2024学年浙江省杭州市八年级(下)开学考试模拟卷
解析卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列学校的校徽图案是轴对称图形的是( )
A. B.
C. D.
【分析】根据如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴进行分析即可.
【解答】解:A,C,D选项中的图形都不能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以不是轴对称图形;
B选项中的图形能找到这样的一条直线,使图形沿一条直线折叠,直线两旁的部分能够互相重合,所以是轴对称图形;
故选:B.
2.y减去2的差不大于0,用不等式表示为( )
A.y﹣2≤0 B.y﹣2≥0 C.y﹣2<0 D.y﹣2>0
【分析】根据“y减去2的差不大于0”,即可列出关于y的一元一次不等式,此题得解.
【解答】解:根据题意得:y﹣2≤0.
故选:A.
3.已知三角形的两边长分别为5cm和7cm,则第三边的长可以是( )
A.1cm B.2cm C.6cm D.12cm
【分析】设三角形第三边的长是x,由三角形三边关系定理得到2<x<12,即可得到答案.
【解答】解:设三角形第三边的长是x,
∴7﹣5<x<7+5,
∴2<x<12,
∴第三边的长可以6cm.
故选:C.
4.直线y=﹣x+3与x轴的交点坐标是( )
A.(0,3) B.(0,﹣3) C.(3,0) D.(﹣3,0)
【分析】令一次函数的解析式中y=0求出x的值,即可得到直线y=﹣x+3与x轴的交点坐标.
【解答】解:令直线y=﹣x+3中y=0,则﹣x+3=0,
解得x=3,
∴直线y=﹣x+3与x轴的交点坐标为(3,0).
故选:C.
5.下列命题中是真命题的是( )
A.等边三角形一条边上的高线也是该条边上的中线
B.有一个角是60°的三角形是等边三角形
C.等腰三角形一定是锐角三角形
D.有一个角对应相等的两个等腰三角形全等
【分析】由等腰三角形的性质,等边三角形的性质,全等三角形的判定,即可判断.
【解答】解:A、等边三角形一条边上的高线也是该条边上的中线,正确,故A符合题意;
B、有一个角是60°的等腰三角形是等边三角形,故B不符合题意;
C、等腰三角形可能的锐角三角形,直角三角形,钝角三角形,故C不符合题意;
D、有一个角对应相等的两个等腰三角形不一定全等,故D不符合题意.
故选:A.
6.如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )
A.CB=CD B.∠BAC=∠DAC C.∠B=∠D=90° D.∠BCA=∠DCA
【分析】要判定△ABC≌△ADC,已知AB=AD,AC是公共边,具备了两组边对应相等,故添加CB=CD、∠BAC=∠DAC、∠B=∠D=90°后可分别根据SSS、SAS、HL能判定△ABC≌△ADC,而添加∠BCA=∠DCA后则不能.
【解答】解:A、添加CB=CD,根据SSS,能判定△ABC≌△ADC,故A选项不符合题意;
B、添加∠BAC=∠DAC,根据SAS,能判定△ABC≌△ADC,故B选项不符合题意;
C、添加∠B=∠D=90°,根据HL,能判定△ABC≌△ADC,故C选项不符合题意;
D、添加∠BCA=∠DCA时,不能判定△ABC≌△ADC,故D选项符合题意;
故选:D.
7.点M在第四象限,点M到x轴的距离为3,到y轴的距离为4,则M点坐标是( )
A.(4,﹣3) B.(4,3) C.(3,﹣4) D.(﹣3,4)
【分析】根据第四象限的点的坐标特征,以及点到y轴的距离等于横坐标的绝对值,到x轴的距离等于纵坐标的绝对值,求出点M的横坐标与纵坐标即可得解.
【解答】解:∵点M在第四象限,且点M到x轴的距离为3,到y轴的距离为4,
∴点M的横坐标为4,纵坐标为﹣3,
∴点M的坐标为(4,﹣3).
故选:A.
8.如图,在同一平面直角坐标系中,一次函数y=k1x+b1与y=k2x+b2(其中k1k2≠0)的图象分别为直线l1和直线l2,下列结论中一定正确的是( )
A.k1+k2<0 B.k1k2>0 C.b1+b2<0 D.b1b2>0
【分析】根据一次函数y=k1x+b1与y=k2x+b2的图象位置,可得k1>0,b1>0,k2>0,b2<0,然后逐一判断即可解答.
【解答】解:∵一次函数y=k1x+b1的图象过第一、二、三象限,
∴k1>0,b1>0,
∵一次函数y=k2x+b2的图象过第一、三、四象限,
∴k2>0,b2<0,且|b1|>|b2|,
∵A、k1+k2<0,
故A不符合题意;
B、k1k2>0,
故B符合题意;
C、b1+b2>0,
故C不符合题意;
D、b1 b2<0,
故D不符合题意;
故选:B.
9.“激情马拉松 活力好青年”,2023年12月10日,诸暨西施马拉松鸣笛开跑.在比赛过程中,乙选手匀速跑完全程,甲选手1.5h后的速度为10km/h,甲、乙两选手的部分行程y(km)随起跑的时间x(h)变化的图象如图所示.下列说法中正确的个数有( )
①起跑后半小时内甲的速度为16km/h;
②第1小时两人都跑了10km;
③图中记录的两人所跑路程都为20km;
④图中所示的截止行程点处乙比甲早到0.2h.
A.1个 B.2个 C.3个 D.4个
【分析】①根据速度=路程÷时间计算即可;
②根据两图象的交点坐标作答即可;
③图中记录的两人所跑路程相等,根据乙的路程=乙的速度×乙的时间计算即可;
④设当x=a时,三个时间段0≤x<0.5、0.5≤x<1.5、1.5≤x≤a的路程之和为20km,列方程并求解,计算a﹣2的值即可.
【解答】解:当0≤x≤0.5时,甲的速度为8÷0.5=16(km/h),
∴①正确;
根据两图象的交点坐标可知,当x=1时,y=10,
∴②正确;
乙的速度为10÷1=10(km/h),当x=2时,乙所跑的路程为10×2=20(km),
∴③正确;
当0.5<x≤1.5时,甲的速度为(10﹣8)÷(1﹣0.5)=4(km/h),
设当x=a时,甲所跑的路程为20km,则8+4×(1.5﹣0.5)+10×(a﹣1.5)=20,解得a=2.3,
2.3﹣2=0.3(h),
∴图中所示的截止行程点处乙比甲早到0.3h,
∴④不正确;
综上,①②③正确,
故选:C.
10.如图,在△ABC中,∠ACB=90°,以△ABC的各边为边作三个正方形,点G落在HI上,若AC+BC=7,空白部分面积为10,则AB的长为( )
A. B. C. D.
【分析】由正方形的性质推出AB=AF,∠BAN=∠F=90°,由余角的性质推出∠ABN=∠MAF,由ASA证明△BAN≌△AFM,得到△BAN的面积=△AFM的面积,因此四边形FNCM的面积=△ABC的面积,得到空白部分的面积=正方形ABGF的面积﹣2×△ABC的面积,因此AB2﹣2×AC BC=10①,由完全平方公式得AC2+BC2+2AC BC=49,由勾股定理得到AB2+2AC BC=49②,于是AB2=23,即可求出AB的长.
【解答】解:∵四边形ABGF是正方形,
∴AB=AF,∠BAN=∠F=90°,
∴∠MAF+∠BAC=90°,
∵∠ACB=90°,
∴∠ABN+∠BAC=90°,
∴∠ABN=∠MAF,
∵AB=AF,∠BAN=∠F,
∴△BAN≌△AFM(ASA),
∴△BAN的面积=△AFM的面积,
∴四边形FNCM的面积=△ABC的面积,
∴空白部分的面积=正方形ABGF的面积﹣2×△ABC的面积,
∴AB2﹣2×AC BC=10①,
∵AC+BC=7,
∴(AC+BC)2=72,
∴AC2+BC2+2AC BC=49,
∵AB2=AC2+BC2,
∴AB2+2AC BC=49②,
由①和②得AB2=23,
∴AB=(舍去负值).
故选:A.
二.填空题(共6小题,满分24分,每小题4分)
11.在平面直角坐标系中,点(3,2)关于x轴对称的点的坐标为 (3,﹣2) .
【分析】根据“关于x轴对称的点,横坐标相同,纵坐标互为相反数”解答即可.
【解答】解:点(3,2)关于x轴对称的点的坐标为(3,﹣2).
故答案为:(3,﹣2).
12.函数的自变量x的取值范围是 x≠﹣2 .
【分析】根据分式的分母不为0可得x+2≠0,即可得出答案.
【解答】解:由题意得:x+2≠0,
解得:x≠﹣2.
故答案为:x≠﹣2.
13.将“对顶角相等”改写为“如果…那么…”的形式,可写为 如果两个角是对顶角,那么它们相等 .
【分析】命题中的条件是两个角相等,放在“如果”的后面,结论是这两个角的补角相等,应放在“那么”的后面.
【解答】解:题设为:对顶角,结论为:相等,
故写成“如果…那么…”的形式是:如果两个角是对顶角,那么它们相等;
故答案为:如果两个角是对顶角,那么它们相等.
14.将直线y=2x向上平移5个单位后,所得直线对应的函数表达式是 y=2x+5 .
【分析】根据平移法则上加下减可得出平移后的解析式.
【解答】解:将直线y=2x向上平移5个单位后,所得直线的函数表达式是:y=2x+5.
故答案为:y=2x+5.
15.若关于x的不等式组只有一个整数解,则实数a的取值范围是 0<a≤1 .
【分析】先解出不等式组中每个不等式的解集,再根据关于x的不等式组只有一个整数解,即可得到a的取值范围.
【解答】解:,
解不等式①,得:x≥a,
解不等式②,得:x≤,
∵关于x的不等式组只有一个整数解,
∴0<a≤1,
故答案为:0<a≤1.
16.勾股定理的证明方法多样,如图是“水车翼轮法”证明勾股定理:将正方形ACFG沿分割线JK,LM分割成四个全等四边形,再将这四个四边形和正方形ABED拼成大正方形BCHI.若AB=2,,则AL的长为 .
【分析】根据勾股定理求出AC的长,再根据题意得出OP=AL,NP=GL,得出AG﹣AL=OP+ON,即可推出结果.
【解答】解:如图,
在Rt△ABC中,由勾股定理得,
AC=,
∴AG=AC=5,
∵将正方形ACFG沿分割线JK,LM分割成四个全等四边形,再将这四个四边形和正方形ABED拼成大正方形BCHI.
∴OP=AL,NP=GL,
∴AG﹣AL=OP+ON,
∴5﹣AL=AL+2,
∴AL=,
故答案为:.
三.解答题(共8小题,满分66分)
17.(6分)在方格纸中,点P、Q都在格点上,请用无刻度的直尺按要求画格点三角形:
(1)在图1中,画一个以PQ为腰的等腰△APQ(A为格点);
(2)在图2中,画一个以PQ为底的等腰△BPQ(B为格点).
【分析】(1)根据等腰三角形的定义画出图形;
(2)根据等腰直角三角形的判定画出图形.
【解答】解:(1)如图1中,△ABC即为所求(答案不唯一);
(2)如图2中,△BPQ即为所求(答案不唯一).
18.(6分)解不等式(组):
(1)3x+1≥﹣5;
(2).
【分析】(1)不等式移项、合并同类项,系数化为1即可得;
(2)分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.
【解答】解:(1)3x+1≥﹣5,
3x≥﹣5﹣1,
3x≥﹣6,
x≥﹣2;
(2),
解不等式①,得,
解不等式②,得x>2,
故不等式组的解集为.
19.(6分)如图,在△ABC中,AD是△ABC的高线,AE是△ABC的角平分线.
(1)若∠B=60°,∠C=40°,求∠DAE的度数.
(2)若∠B=α,∠C=β(α>β),请直接写出∠DAE的度数(用含α,β的代数式表示).
【分析】(1)由高线可得∠ADB=90°,再由三角形的内角和可求得∠BAD=30°,∠BAC=80°,利用角平分线的定义可求得∠BAE=40°,从而可求∠DAE的度数;
(2)参照(1)进行求解即可.
【解答】解:(1)∵AD是△ABC的高线,
∴∠ADB=90°,
∵∠B=60°,∠C=40°,
∴∠BAD=180°﹣∠B﹣∠ADB=30°,
∠BAC=180°﹣∠B﹣∠C=80°,
∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=40°,
∴∠DAE=∠BAE﹣∠BAD=10°;
(2)∵AD是△ABC的高线,
∴∠ADB=90°,
∵∠B=α,∠C=β,
∴∠BAD=180°﹣∠B﹣∠ADB=90°﹣α,
∠BAC=180°﹣∠B﹣∠C=180°﹣α﹣β,
∵AE是△ABC的角平分线,
∴∠BAE=∠BAC=90°﹣,
∴∠DAE=∠BAE﹣∠BAD=.
20.(8分)已知A(﹣3,0),B(5,0),C(x,y).
(1)若点C在第二象限内,且|x|=3,|y|=3,求点C的坐标,并求△ABC的面积;
(2)若点C在第四象限内,且△ABC的面积为8,|x|=4,求点C的坐标.
【分析】(1)因为点C在第二象限内,所以x<0,y>0,因为|x|=3,|y|=3,所以x=﹣3,y=3,即点C的坐标为(﹣3,3),再根据点A(﹣3,0),B(5,0)的坐标,即可得出△ABC的面积;
(2)因为△ABC的面积为8,点C在第四象限内,所以×8×(﹣y)=8,得y=﹣2,由|x|=4,得x=4,即可得出点C的坐标.
【解答】解:(1)∵点C在第二象限内,
∴x<0,y>0,
∵|x|=3,|y|=3,
∴x=﹣3,y=3,
∴点C的坐标为(﹣3,3),
∵A(﹣3,0),B(5,0),
∴△ABC的面积=×8×3=12;
(2)∵△ABC的面积为8,点C在第四象限内,
∴×8×(﹣y)=8,
∴y=﹣2,
∵|x|=4,
∴x=4,
∴点C的坐标为(4,﹣2).
21.(8分)已知:如图,在△ABC中,AB=2AC,过点C作CD⊥AC,交∠BAC的平分线于点D.求证:∠BAC=2∠ABD.
【分析】根据角平分线的性质可得DE=DC,再利用三角形全等可得AE=AC,进而得出DE是AB的中垂线,由中垂线的性质和角平分线的定义可得结论.
【解答】解:过点D作DE⊥AB于E,
∵AD平分∠BAC,DE⊥AB,DC⊥AC,
∴DE=DC,
在Rt△AED和Rt△ACD中,
∵DE=DC,AD=AD,
∴Rt△AED≌Rt△ACD(HL),
∴AE=AC,
又∵AB=2AC,
∴AE=BE,
∴DE是AB的中垂线,
∴DA=DB,
∴∠ABD=∠BAD,
∵∠BAD=∠CAD=∠BAC,
∴∠ABD=∠BAC,
即∠BAC=2∠ABD.
22.(10分)随着梦天实验舱的顺利发射,我国空间站完成了在轨组装,为了庆祝这令人激动的时刻,某校开展了关于空间站的科学知识问答竞赛.为了奖励在竞赛中表现优异的学生,学校准备一次性购买A,B两种航天器模型作为奖品.已知购买1个A模型和1个B模型共需159元;购买3个A模型和2个B模型共需374元.
(1)求A模型和B模型的单价;
(2)根据学校的实际情况,需一次性购买A模型和B模型共20个,但要求购买A模型的数量多于12个,且不超过B模型的3倍.请你给出一种费用最少的方案,并求出该方案所需的费用.
【分析】(1)设A模型的单价是x元,B模型的单价是y元,根据“购买1个A模型和1个B模型共需159元;购买3个A模型和2个B模型共需374元”,可列出关于x,y的二元一次方程组,解之即可得出结论;
(2)设购买m个A模型,则购买(20﹣m)个B模型,根据“购买A模型的数量多于12个,且不超过B模型的3倍”,可列出关于m的一元一次不等式组,解之可得出m的取值范围,结合m为正整数,可得出各购买方案,再求出各方案所需费用,比较后即可得出结论.
【解答】解:(1)设A模型的单价是x元,B模型的单价是y元,
根据题意得:,
解得:.
答:A模型的单价是56元,B模型的单价是103元;
(2)设购买m个A模型,则购买(20﹣m)个B模型,
根据题意得:,
解得:12<m≤15,
又∵m为正整数,
∴m的值为13,14,15,
∴该学校共有3种购买方案,
方案1:购买13个A模型,7个B模型,所需费用为56×13+103×7=1449(元);
方案2:购买14个A模型,6个B模型,所需费用为56×14+103×6=1402(元);
方案3:购买15个A模型,5个B模型,所需费用为56×15+103×5=1355(元),
∵1449>1402>1355,
∴购买15个A模型,5个B模型费用最少,该方案所需的费用为1355元.
23.(10分)如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与x轴交于点A(﹣2,0),与y轴交于点B,且与正比例函数的图象交于点C(m,3).
(1)求m的值和一次函数y=kx+b的表达式;
(2)若点P是y轴上一点,且S△PBC=2S△OBC,求点P的坐标.
【分析】(1)将点C(m,3)代入可得m=4,再用待定系数法求一次函数的解析式即可;
(2)由y=x+1可求得B的坐标,即可利用三角形面积求得S△OBC=,根据S△PBC=2S△OBC得到BP 3=3,解得BP=2,进而即可求得P的坐标.
【解答】解:(1)∵将点C(m,3)代入,
∴3=m,
∴m=4,
∴C(4,3),
将A(﹣2,0),C(4,3)代入一次函数的解析式为y=kx+b得:
,
解得,
∴一次函数y=kx+b的表达式为y=x+1;
(2)令x=0,则y=x+1=1,
∴B(0,1),
∴OB=1,
∴S△OBC=OB xC=,
∵S△PBC=2S△OBC,
∴S△BPC=BP xC=3,即BP 3=3,
∴BP=2,
∴点P的坐标为(0,3)或(0,﹣1).
24.(12分)在四边形ABCD中,AB=BC=CD,∠BCD=60°,∠ABC=α(60°<α<180°),E为AD中点,连接AC,BE交于点F.
(1)当α=100°时,∠BAC= 40° ,∠ABF= 20° ;
(2)当α的大小改变时,∠BFC的度数是否发生改变?若变化,求∠BFC的变化范围,若不变,求∠BFC的度数;
(3)猜想AF,BF,CF之间的数量关系,并说明理由;
(4)若S△ABF:S△CBF=3:8,则= .
【分析】(1)根据等腰三角形的性质即可求出∠BAC的度数,根据,可以求出∠ABF的度数;
(2)连接BD,求出△BCD是等边三角形,分别表示出∠ABE,∠BAC,即可求解;
(3)如图,作∠FBG=60°,BG交AC于点G,求出△BFG是等边三角形,再证明△AFB≌△CGB(AAS),从而得出AF,BF,CF之间的数量关系;
(4)根据,设AF=3a,CF=8a,结合(3)得出BF=GF=CF﹣CG=5a,再根据∠CAE=30°,由30度直角三角形性质得出,由此即可解题.
【解答】解:(1)∵AB=BC,∠ABC=α=100°,
∴∠BAC=∠BCA=40°,
如图,连接BD
∵BC=CD,∠BCD=60°,
∴△BCD是等边三角形
∴BD=CD=AD,∠CBD=60°,
又∵E为AD中点,
∴,
∵AB=BC,
∴.
∴.
∵∠BFC=∠BAC+∠ABF,
∴∠ABF=60°﹣40°=20°.
故答案为:40°,20°;
(2)结论:不变,
证明:如图,连接BD,
∵BC=CD,∠BCD=60°,
∴△BCD是等边三角形,
∴BD=CD=AD,∠CBD=60°,
又∵E为AD中点,
∴,
∵AB=BC,
∴.
∴;
(3)如图,作∠FBG=60°,BG交AC于点G.
∵∠BFC=60°,∠FBG=60°,
∴△BFG是等边三角形,
∴∠BGF=60°,BF=FG,
∴∠BGC=∠BFA=120°,
∵AB=BC,
∴∠BAC=∠BCA,
∴△AFB≌△CGB(AAS),
∴AF=GC,
∵CG+CF=CF,AF=GC,BF=FG,
∴AF+BF=CF.
(4)∵,
∴设AF=3a,CF=8a,
由(3)得:AF+BF=CF,
∴BF=CF﹣AF=5a,
∵BA=BD,E为AD中点,
∴BE⊥AD,
由(2)知∠BFC=60°,
∴∠AFE=∠BFC=60°,
∴∠CAE=30°,
在Rt△AFE中,∠CAE=30°,
∴,
∴.
故答案为:.
同课章节目录
