2009年中考四边形的考点分析
图片预览








文档简介
课件40张PPT。
四边形的考点分析
景宁城北中学 陈呈慧
2009年3月20日 2009年初中数学学业考试 ▲ 2008年浙江省初中数学学业考 试“四边形”考题分析
▲ “四边形”考点分析
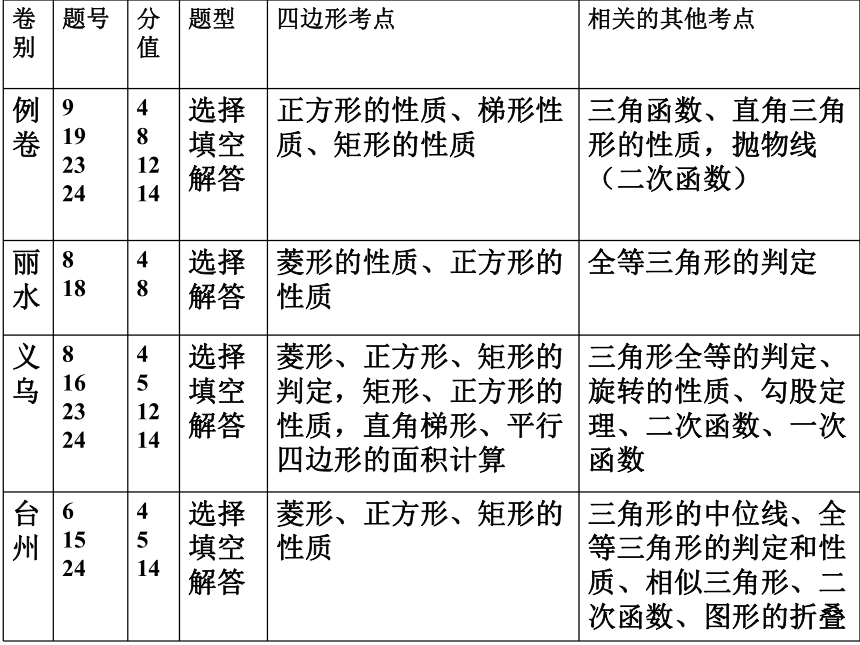
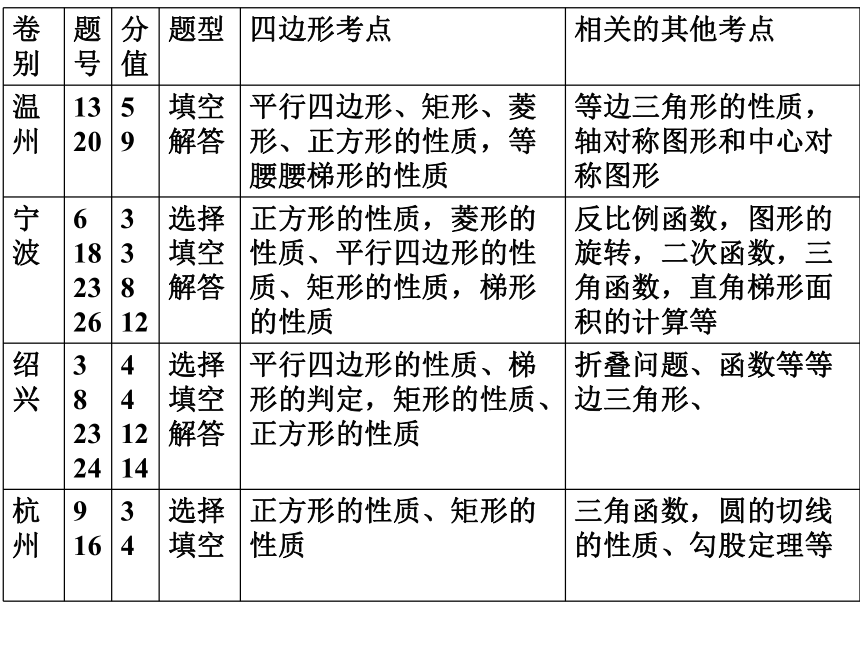
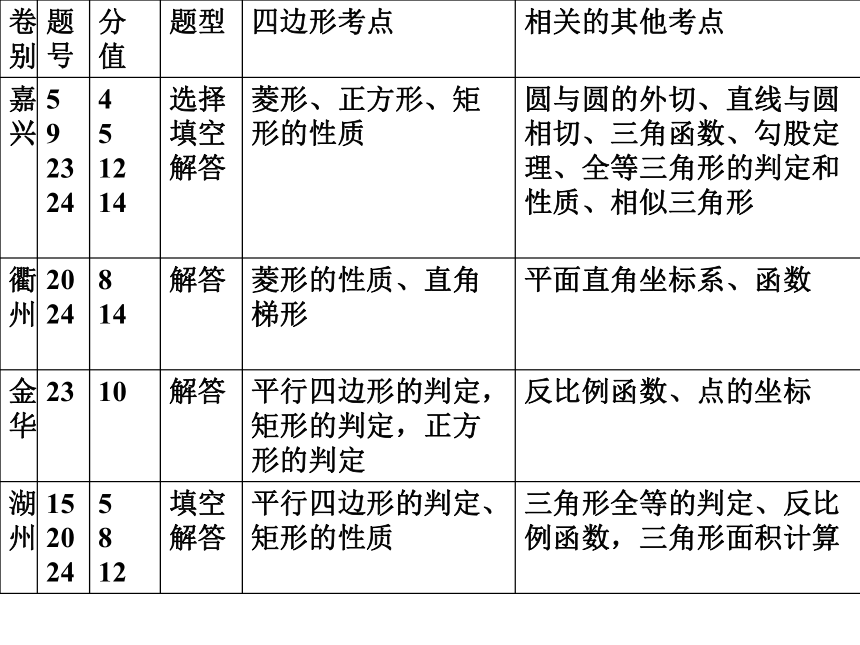
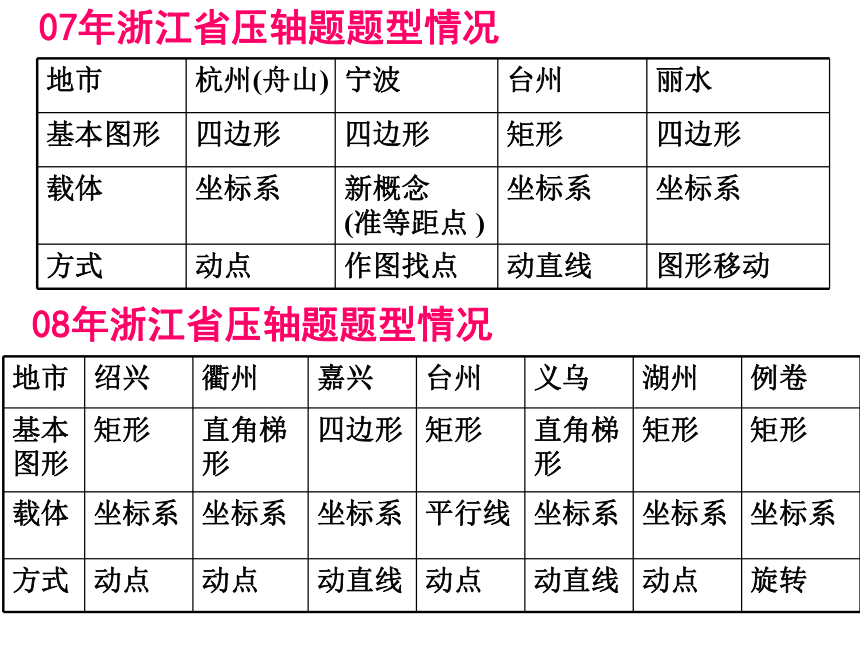
▲ “四边形”备考建议 一、2008年浙江省初中数学学业考试 “四边形” 试题分析 浙江省2008年的所有试卷和中考说明的例卷中,平均分为24.25,其中杭州卷所占的分值最少,只考了7分,并且只有选择和填空,而例卷、绍兴卷、嘉兴卷、义乌卷等都在34分以上,在题形上有填空、选择及解答题,衢州卷、金华卷只有解答题,而绍兴、衢州、湖州、嘉兴、台州、义乌、例卷等压轴题的基本图形是矩形和直角梯形,结合坐标系。 07年浙江省压轴题题型情况08年浙江省压轴题题型情况 二、“四边形”考点分析 1、通过已知多边形的内角和求多边
的边数,来考查n(n≥3)边形的内角和
是(n-2)·180°,外角和都是360°。
二、“四边形”考点分析 2、通过用多边形进行地面的铺设,
考查任意一个三角形、四边形或正六边
形可以镶嵌平面。【 2008黑龙江哈尔滨】 某商店出售下列四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形。若只选购其中一种地砖镶嵌地面,可供选择的地砖共有( )(A)4种 (B)3种 (C)2种 (D)1种【 2008湖北 恩施】为了让州城居民有更多休闲和娱乐的地方,政府又新建了几处广场,工人师傅在铺设地面时,准备选用同一种正多边形地砖.现有下面几种形状的正多边形地砖,其中不能进行平面镶嵌的是( )A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形 二、 “四边形”考点分析3、考查平行四边形、矩形、菱形、正方形的有关性质 (1)通过对线段的长度、角度的大小、图形的面积
等的计算来考查对性质的理解和直接运用,考察学
生的基础知识和基本技能。
【 2008台州】 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=a,
则菱形ABCD的周长为( )A.16a B.12a C.8a D.4a 【 2008丽水】 如图,在三角形中,AB>AC,D、E分别是AB、AC上的点,△ADE 沿线段DE翻折,使A点落在边BC上,记为A/.若四边形AD A/ E是菱形,则下列说法正确的是( ) A.AA/是△ABC的中位线 B. AA/是BC边上的中线
C. AA/是BC边上的高 D. AA/是△ABC的角平分线【 2008宁波】 如图,菱形OABC中,∠A =120o,OA=1,将菱形OABC绕点O按顺时针方向旋转90o,则图中由 围成的阴影部分的面积是 . 【 2008重庆市】如图,在□ABCD中,
AB=5cm,BC=4cm, 则□ABCD的
周长为 cm. 二、“四边形”考点分析(2)通过对以四边形为背景,结合
函数、折叠、旋转变换,动点问题的
求解,考查对性质的灵活运用。
(2008义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断(2)将原题中正方形改为矩形(如图4—6),且AB=a,BC=b,CE=ka, CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结、,且a=3,b=2,k=,求 的值。
二、 “四边形”考点分析4、平行四边形、矩形、菱形、正方形的判定 (1)通过对某种特殊四边形进行简单的
推理和论证,以及对命题的编制来考查判
定定理和各个特殊四边形之间的关系。 (2008湖州)如图,在△CDF中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
(1)求证:△BDE≌△CDF.
(2)请连结BF,CE,试判断四边形BECF是何种特殊四边形,并说明理由. (08年江苏徐州 )已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断
① OA=OC ② AB=CD ③ ∠BAD=∠DCB ④ AD∥BC
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
①构造一个真命题,画图并给出证明;
②构造一个假命题,举反例加以说明(3)将四边形的性质和判定有机的结合,通过创设开放性试题、将图形中的一部分进行变换、进行拓展、探究,挖掘其中的不变因素,考查对性质的综合运用能力。 二、“四边形”考点分析(08浙江嘉兴)小丽参加数学兴趣小组活动,提供了下面3个有联系的问题,请你帮助解决:
(1)如图1,正方形ABCD中,作AE交BC于E,DF⊥AE交AB 于F,求证:AE=DF;
(2)如图2,正方形ABCD中,点E,F分别在AD,BC上,点G,H分别在AB,CD上,且EF⊥GH,求 的值;
(3)如图3,矩形ABCD中,AB=a,BC=b,点E,F分别在AD,BC上,且EF⊥GH,求 的值. 二、“四边形”考点分析5、梯形的性质和判定,特别等腰梯形的有
关性质和等腰梯形判定 。 除了注重基础知识的考查,也注重
对学生空间想象能力、运算能力、转化
的思想、分类讨论的思想的考查。 (2008,绍兴)如图,沿虚线将剪开,则得到的四边形是( )
A.梯形 B.平行四边形
C.矩形 D.菱形(1)注重考查平行四边形和梯形间的区别(2)将图形变换的知识融入到梯形中,考查学生的双基 【 2008云南省】如图 ,在梯形ABCD中,AD∥BC,AB=DC,若点M为线段AD上任意一点 (M与A,D不重合).问:当点M在什么位置时,MB=MC,请说明理由.(3)将平行线的性质、等腰梯形的性质和判定及四边形的性质等有机地整合到有一起(4)通过对以梯形为背景设置的动点问题、折叠问题的求解,考查等腰梯形的性质和判定、梯形面积的计算等。(08苏州市)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
(1)梯形ABCD的面积等于 ;
(2)当PQ//AB时,P点离开D点的时间等于 秒;
(3)当P、Q、C三点构成直角三角形时,P点离开D点多少时间?1、整理知识,构建体系
2、立足教材,突出基础性,抓住最本质、最核心知识
3、注重思维的严谨性,提高学生的数学能力
4、创设开放题、探究题,注重学生综合能力的培养
5、注重问题的探究过程,提高学生的思维品质。三、备考建议 “四边形”:注重性质考查;注重与图形变换结合和应用;突出对推理能力考查1、已知:矩形ABCD的对角线AC、BD相交
于点O,∠AOD=120°,AB=6cm,那么对
角线的长 。O2、如图:是一个风筝的平面示意图,四边形
ABCD是等腰梯形,E、F、G、H分别是各边的中点,假设图中阴影部分所需的布料的面积为S1,其它部分所需布料的面积之和为S2(边缘外的布料不计)则 ( )
A. S1>S2 B.S1<S2
C.S1=S2 D.不确定 3、已知:四边形ABCD是平行四边形, E、
F是对角线AC上的点
(1)如果 ,则四边形DEBF是平行四
边形(只要填一个就可以)
(2)证明你的结论3、如图①,在矩形ABCD中,AB=20cm,BC=4cm,点P从点A开始沿路线A→B→C→D以4cm/s的速度移动,点Q从点C开始沿路线CD以1cm/s的速度移动,如果点P,Q分别从A,C同时出发,当其中一点到达D时,另一点也随之停止运动。设运动时间为t(s)。
(1)t为何值时,四边形APQD为矩形?
(2)设A,P,D,Q四点围成的四边形的面积为S,求出S关于t的函数关系式及t的取值范围;
(3)如图②,如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?再见!
四边形的考点分析
景宁城北中学 陈呈慧
2009年3月20日 2009年初中数学学业考试 ▲ 2008年浙江省初中数学学业考 试“四边形”考题分析
▲ “四边形”考点分析
▲ “四边形”备考建议 一、2008年浙江省初中数学学业考试 “四边形” 试题分析 浙江省2008年的所有试卷和中考说明的例卷中,平均分为24.25,其中杭州卷所占的分值最少,只考了7分,并且只有选择和填空,而例卷、绍兴卷、嘉兴卷、义乌卷等都在34分以上,在题形上有填空、选择及解答题,衢州卷、金华卷只有解答题,而绍兴、衢州、湖州、嘉兴、台州、义乌、例卷等压轴题的基本图形是矩形和直角梯形,结合坐标系。 07年浙江省压轴题题型情况08年浙江省压轴题题型情况 二、“四边形”考点分析 1、通过已知多边形的内角和求多边
的边数,来考查n(n≥3)边形的内角和
是(n-2)·180°,外角和都是360°。
二、“四边形”考点分析 2、通过用多边形进行地面的铺设,
考查任意一个三角形、四边形或正六边
形可以镶嵌平面。【 2008黑龙江哈尔滨】 某商店出售下列四种形状的地砖:①正三角形;②正方形;③正五边形;④正六边形。若只选购其中一种地砖镶嵌地面,可供选择的地砖共有( )(A)4种 (B)3种 (C)2种 (D)1种【 2008湖北 恩施】为了让州城居民有更多休闲和娱乐的地方,政府又新建了几处广场,工人师傅在铺设地面时,准备选用同一种正多边形地砖.现有下面几种形状的正多边形地砖,其中不能进行平面镶嵌的是( )A. 正三角形 B. 正方形 C. 正五边形 D. 正六边形 二、 “四边形”考点分析3、考查平行四边形、矩形、菱形、正方形的有关性质 (1)通过对线段的长度、角度的大小、图形的面积
等的计算来考查对性质的理解和直接运用,考察学
生的基础知识和基本技能。
【 2008台州】 如图,在菱形ABCD中,对角线AC,BD相交于点O,E为AB的中点,且OE=a,
则菱形ABCD的周长为( )A.16a B.12a C.8a D.4a 【 2008丽水】 如图,在三角形中,AB>AC,D、E分别是AB、AC上的点,△ADE 沿线段DE翻折,使A点落在边BC上,记为A/.若四边形AD A/ E是菱形,则下列说法正确的是( ) A.AA/是△ABC的中位线 B. AA/是BC边上的中线
C. AA/是BC边上的高 D. AA/是△ABC的角平分线【 2008宁波】 如图,菱形OABC中,∠A =120o,OA=1,将菱形OABC绕点O按顺时针方向旋转90o,则图中由 围成的阴影部分的面积是 . 【 2008重庆市】如图,在□ABCD中,
AB=5cm,BC=4cm, 则□ABCD的
周长为 cm. 二、“四边形”考点分析(2)通过对以四边形为背景,结合
函数、折叠、旋转变换,动点问题的
求解,考查对性质的灵活运用。
(2008义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:
(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断(2)将原题中正方形改为矩形(如图4—6),且AB=a,BC=b,CE=ka, CG=kb (a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由.
(3)在第(2)题图5中,连结、,且a=3,b=2,k=,求 的值。
二、 “四边形”考点分析4、平行四边形、矩形、菱形、正方形的判定 (1)通过对某种特殊四边形进行简单的
推理和论证,以及对命题的编制来考查判
定定理和各个特殊四边形之间的关系。 (2008湖州)如图,在△CDF中,D是BC边的中点,F,E分别是AD及其延长线上的点,CF∥BE.
(1)求证:△BDE≌△CDF.
(2)请连结BF,CE,试判断四边形BECF是何种特殊四边形,并说明理由. (08年江苏徐州 )已知四边形ABCD的对角线AC与BD交于点O,给出下列四个论断
① OA=OC ② AB=CD ③ ∠BAD=∠DCB ④ AD∥BC
请你从中选择两个论断作为条件,以“四边形ABCD为平行四边形”作为结论,完成下列各题:
①构造一个真命题,画图并给出证明;
②构造一个假命题,举反例加以说明(3)将四边形的性质和判定有机的结合,通过创设开放性试题、将图形中的一部分进行变换、进行拓展、探究,挖掘其中的不变因素,考查对性质的综合运用能力。 二、“四边形”考点分析(08浙江嘉兴)小丽参加数学兴趣小组活动,提供了下面3个有联系的问题,请你帮助解决:
(1)如图1,正方形ABCD中,作AE交BC于E,DF⊥AE交AB 于F,求证:AE=DF;
(2)如图2,正方形ABCD中,点E,F分别在AD,BC上,点G,H分别在AB,CD上,且EF⊥GH,求 的值;
(3)如图3,矩形ABCD中,AB=a,BC=b,点E,F分别在AD,BC上,且EF⊥GH,求 的值. 二、“四边形”考点分析5、梯形的性质和判定,特别等腰梯形的有
关性质和等腰梯形判定 。 除了注重基础知识的考查,也注重
对学生空间想象能力、运算能力、转化
的思想、分类讨论的思想的考查。 (2008,绍兴)如图,沿虚线将剪开,则得到的四边形是( )
A.梯形 B.平行四边形
C.矩形 D.菱形(1)注重考查平行四边形和梯形间的区别(2)将图形变换的知识融入到梯形中,考查学生的双基 【 2008云南省】如图 ,在梯形ABCD中,AD∥BC,AB=DC,若点M为线段AD上任意一点 (M与A,D不重合).问:当点M在什么位置时,MB=MC,请说明理由.(3)将平行线的性质、等腰梯形的性质和判定及四边形的性质等有机地整合到有一起(4)通过对以梯形为背景设置的动点问题、折叠问题的求解,考查等腰梯形的性质和判定、梯形面积的计算等。(08苏州市)如图,在等腰梯形ABCD中,AD∥BC,AB=DC=5,AD=6,BC=12.动点P从D点出发沿DC以每秒1个单位的速度向终点C运动,动点Q从C点出发沿CB以每秒2个单位的速度向B点运动.两点同时出发,当P点到达C点时,Q点随之停止运动.
(1)梯形ABCD的面积等于 ;
(2)当PQ//AB时,P点离开D点的时间等于 秒;
(3)当P、Q、C三点构成直角三角形时,P点离开D点多少时间?1、整理知识,构建体系
2、立足教材,突出基础性,抓住最本质、最核心知识
3、注重思维的严谨性,提高学生的数学能力
4、创设开放题、探究题,注重学生综合能力的培养
5、注重问题的探究过程,提高学生的思维品质。三、备考建议 “四边形”:注重性质考查;注重与图形变换结合和应用;突出对推理能力考查1、已知:矩形ABCD的对角线AC、BD相交
于点O,∠AOD=120°,AB=6cm,那么对
角线的长 。O2、如图:是一个风筝的平面示意图,四边形
ABCD是等腰梯形,E、F、G、H分别是各边的中点,假设图中阴影部分所需的布料的面积为S1,其它部分所需布料的面积之和为S2(边缘外的布料不计)则 ( )
A. S1>S2 B.S1<S2
C.S1=S2 D.不确定 3、已知:四边形ABCD是平行四边形, E、
F是对角线AC上的点
(1)如果 ,则四边形DEBF是平行四
边形(只要填一个就可以)
(2)证明你的结论3、如图①,在矩形ABCD中,AB=20cm,BC=4cm,点P从点A开始沿路线A→B→C→D以4cm/s的速度移动,点Q从点C开始沿路线CD以1cm/s的速度移动,如果点P,Q分别从A,C同时出发,当其中一点到达D时,另一点也随之停止运动。设运动时间为t(s)。
(1)t为何值时,四边形APQD为矩形?
(2)设A,P,D,Q四点围成的四边形的面积为S,求出S关于t的函数关系式及t的取值范围;
(3)如图②,如果⊙P和⊙Q的半径都是2cm,那么t为何值时,⊙P和⊙Q外切?再见!
同课章节目录
