2009年中考图形与证明考法分析
图片预览





文档简介
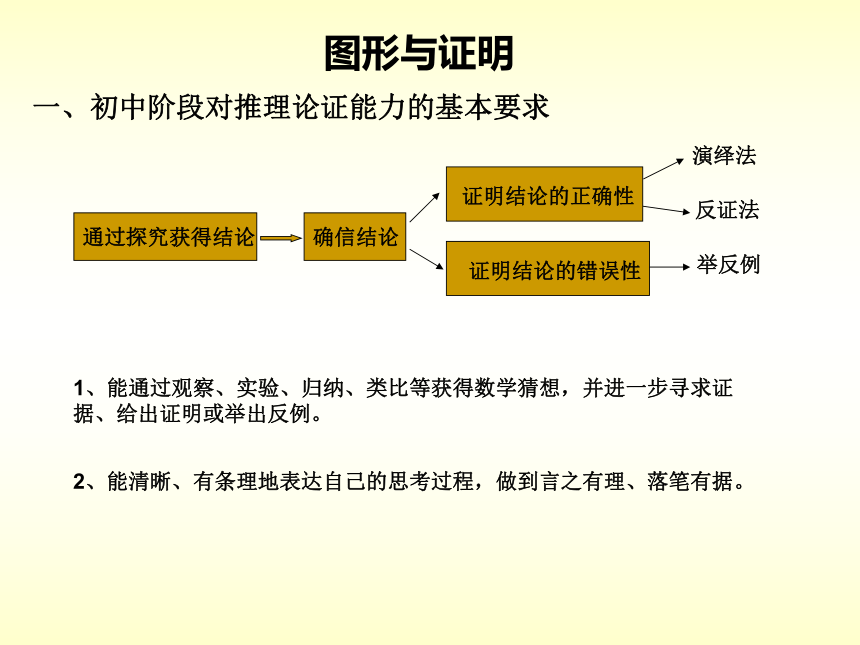
课件18张PPT。图 形 与 证 明2009年丽水市初三数学考试与评价研讨会专题分析青田县章旦中学教育集团 周春丽一、初中阶段对推理论证能力的基本要求图形与证明1、能通过观察、实验、归纳、类比等获得数学猜想,并进一步寻求证据、给出证明或举出反例。2、能清晰、有条理地表达自己的思考过程,做到言之有理、落笔有据。二、考查的基本形式1、借助数、形考查合情推理能力2、着力于演绎推理能力的考查(侧重于三种论证方法及书写格式)3、将合情推理和演绎推理综合起来考查
《标准》强调 对于“证明”,《标准》则要求学生养成“说理有据”的态度、尊重客观事实的精神和质疑的习惯,形成证明的意识,理解证明的必要性和意义,体会证明的思想,掌握证明的基本方法等等,而不是过于追求证明的技巧、证明的速度以及题目的数量和难度。 图形与证明是空间与图形的核心内容之一,它贯穿在整个几何知识的学习及运用之中。
内容主要有:了解定义、命题、定理、互逆命题、反证法的含义;掌握平行线的性质定理和判定定理、全等三角形的性质定理和判定定理、直角三角形全等的判定定理;掌握三角形的内角和定理和推论、角平分线和垂直平分线性质定理及逆定理、三角形中位线定理;掌握等腰三角形、等边三角形、直角三角形性质与判定定理;掌握平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理。§考点聚焦 例1(2008永州)下列命题是假命题的是( )
(A)四个角相等的四边形是矩形
(B)对角线互相平分的四边形是平行四边形
(C)四条边相等的四边形是菱形
(D)对角线互相垂直且相等的四边形是正方形
分析:掌握平行四边形、矩形、菱形、正方形的判定方法是解决本题的关键.
解:选(D)。
点评:本题考查对平行四边形及特殊的平行四边形的判定方法的把握,遇到这种题,可将其中的文字语言转化为图形语言,便能迅速作出准确判断。§考点一 定义、命题、定理、互逆命题、反证法的考查。§考点2 平行线的性质定理和判定定理的考查§考点3:全等三角形性质和判定的考查例1(2008郴州)如图1,菱形ABCD中,E,F分别为BC、CD上的点,且CE=CF.求证:AE=AF.
分析:本题中灵活运用菱形的性质:四边相等,两组对角分别相等.每一条对角线平分每一组对角.找到全等三角形的对应元素是解本题的关键.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD, ∠ B=∠D
∵CE=CF,
∴BE=DF.
在 △ ABE与△ ADF中,AB=AD,∠ B=∠D ,
BE=DF。
∴ △ABE≌ △ ADF ,∴AE=AF.
点评:掌握全等三角形的概念和性质,还要能准确辨认全等三角形中的对应元素,通过证明全等来证明线段相等或者角相等.一、把握三角形全等的性质,考查线段相等的证明。例2(2008湘潭)如图2,在正五边形ABCDE中,连结对角线AC、AD和CE,AD交CE于F.
(1)请列出图中两对全等三角形_________________(不另外
添加辅助线);
(2)请选择所列举的一对全等三角形加以证明。
分析:由正多边形的性质可知:正多边形的各边相等,各角相等.这是一类结论不惟一的试题.解决此类问题的关键是依据图形,通过准确辨认全等三角形的对应元素,证明三角形全等.
解:(1)△ABC≌△AED,△ABC≌△EDC;
(2)证明:在正五边形ABCDE中,,
∠EAB=∠B=∠BCD=∠CDE=∠DEA,
故在△ABC与△AED中,AB=AE,∠B=∠DEA,BC=DE,
∴△ABC≌△AED,
在△ABC与△EDC中,AB=ED,∠B=∠CDE,BC=DC, △ABC≌△EDC.
点评:本考题题干简单清晰,但考点的内容与正多边形的知识相结合,需要具有分解基本图形的能力和基本的探究能力,才能顺利解题.二、紧扣三角形全等的判定,考查三角形全等的开放型问题.例3 (2008、丽水)如图,正方形ABCD中,E与F分别是AD、BC 上一点.在①AE=CF、②BE∥DF、③∠1 =∠2中,请选择其中一个条件,证明:BE=DF
(1)你选择的条件是 ▲ (只需填写序号);
(2)证明: 例1 (2008娄底)如图5,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF ∥AB交AC于F.
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
分析:本题主要考查同学们对平行四边形及特殊的平行四边形的判定方法的把握.
证明:(1)∵ DE∥AC ,
∴∠ADE=∠DAF,同理∠DAE= ∠ FDA.
∵AD=DA,
∴△ADE≌△DAF,∴AE=DF.
(2)若AD平分∠BAC,四边形AEDF是菱形.
证明:∵ DE∥AC, DF ∥AB ,
∴四边形AEDF是平行四边形,
∵ ∠FAD= ∠ EAD,∴AF=DF,
∴平行四边形AEDF为菱形.
点评:三角形全等及平行四边形的性质都可以证明两线段相等,此类题起点低,注重基础知识及基本技能的考查,考查了同学们最基本的几何推理证明能力.§考点4:平行四边形、矩形、菱形、正方形、等腰梯形的性质与判定的考查。§考点5 取材于课本中的例、习题的变式试题拓展探究结论1:∠DOB=60°。
结论2:当AB,AC的夹角∠BAC不断变化时,EB,CD的夹角∠BOC保持不变,即∠BOC=120°不变。
结论3:若CD边上的高为AF,BE边上的高为AH,则AF=AH。
结论4:若CD边上的中线为AF,BE边上的中线为AH,AF=AH。
结论5:OA是∠DOE的平分线。
结论6:若∠BAC=60°,则①△AMN为等边三角形;②MN∥DE。例2 (08沈阳)已知:如图①所示,在 △ABC 和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
(1)求证:①BE=CD;②△AMN是等腰三角形.
(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转 180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;
(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证: △PBD ∽△AMN例3 (2008义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE。我们探究下列图中线段BG,线段DE的长度关系及所在的位置关系:
(1)①猜想如图1中线段BG,线段DE的长度关系及所在的位置关系;②将图1的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形。请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断例3 (2008义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE。我们探究下列图中线段BG,线段DE的长度关系及所在的位置关系:
(2)将原题中正方形改为矩形(如图4)且AB=a,BC=b, CE=ka, CG=kb(a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?以图5为例简要说明理由.本例还可以作如下操作变式探索:
连结AF,取AF的中点M,连结MD与MG。
① 探索线段MD与MG的数量关系。
② 设正方形ABCD的边长为b,正方形CEFG的边长为a(b≥2a),求△BFD的面积。§考题预测各位同仁多多指教!谢谢大家联系方式:13285782900 学校网址:www.zzjt.net
《标准》强调 对于“证明”,《标准》则要求学生养成“说理有据”的态度、尊重客观事实的精神和质疑的习惯,形成证明的意识,理解证明的必要性和意义,体会证明的思想,掌握证明的基本方法等等,而不是过于追求证明的技巧、证明的速度以及题目的数量和难度。 图形与证明是空间与图形的核心内容之一,它贯穿在整个几何知识的学习及运用之中。
内容主要有:了解定义、命题、定理、互逆命题、反证法的含义;掌握平行线的性质定理和判定定理、全等三角形的性质定理和判定定理、直角三角形全等的判定定理;掌握三角形的内角和定理和推论、角平分线和垂直平分线性质定理及逆定理、三角形中位线定理;掌握等腰三角形、等边三角形、直角三角形性质与判定定理;掌握平行四边形、矩形、菱形、正方形、等腰梯形的性质和判定定理。§考点聚焦 例1(2008永州)下列命题是假命题的是( )
(A)四个角相等的四边形是矩形
(B)对角线互相平分的四边形是平行四边形
(C)四条边相等的四边形是菱形
(D)对角线互相垂直且相等的四边形是正方形
分析:掌握平行四边形、矩形、菱形、正方形的判定方法是解决本题的关键.
解:选(D)。
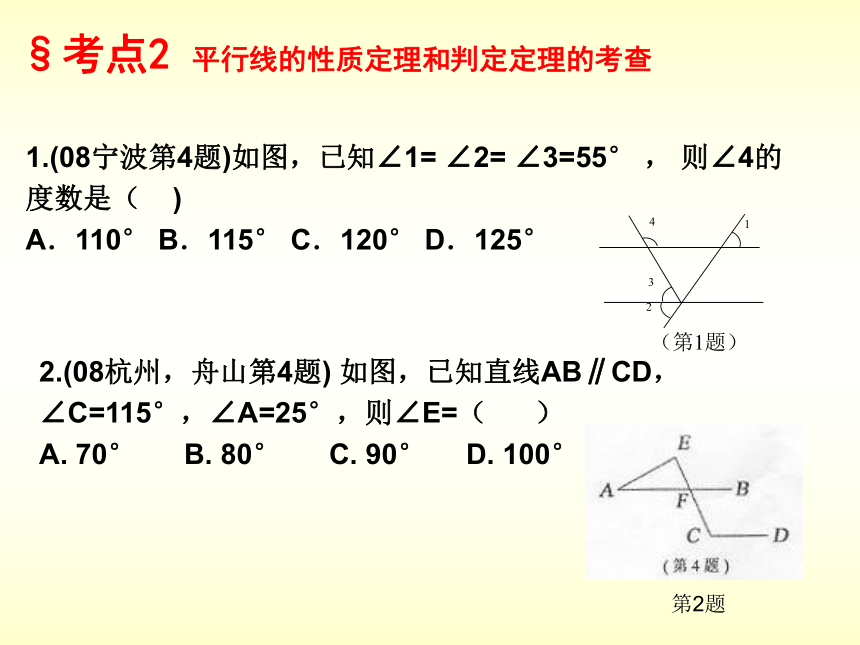
点评:本题考查对平行四边形及特殊的平行四边形的判定方法的把握,遇到这种题,可将其中的文字语言转化为图形语言,便能迅速作出准确判断。§考点一 定义、命题、定理、互逆命题、反证法的考查。§考点2 平行线的性质定理和判定定理的考查§考点3:全等三角形性质和判定的考查例1(2008郴州)如图1,菱形ABCD中,E,F分别为BC、CD上的点,且CE=CF.求证:AE=AF.
分析:本题中灵活运用菱形的性质:四边相等,两组对角分别相等.每一条对角线平分每一组对角.找到全等三角形的对应元素是解本题的关键.
证明:∵四边形ABCD是菱形,
∴AB=BC=CD=AD, ∠ B=∠D
∵CE=CF,
∴BE=DF.
在 △ ABE与△ ADF中,AB=AD,∠ B=∠D ,
BE=DF。
∴ △ABE≌ △ ADF ,∴AE=AF.
点评:掌握全等三角形的概念和性质,还要能准确辨认全等三角形中的对应元素,通过证明全等来证明线段相等或者角相等.一、把握三角形全等的性质,考查线段相等的证明。例2(2008湘潭)如图2,在正五边形ABCDE中,连结对角线AC、AD和CE,AD交CE于F.
(1)请列出图中两对全等三角形_________________(不另外
添加辅助线);
(2)请选择所列举的一对全等三角形加以证明。
分析:由正多边形的性质可知:正多边形的各边相等,各角相等.这是一类结论不惟一的试题.解决此类问题的关键是依据图形,通过准确辨认全等三角形的对应元素,证明三角形全等.
解:(1)△ABC≌△AED,△ABC≌△EDC;
(2)证明:在正五边形ABCDE中,,
∠EAB=∠B=∠BCD=∠CDE=∠DEA,
故在△ABC与△AED中,AB=AE,∠B=∠DEA,BC=DE,
∴△ABC≌△AED,
在△ABC与△EDC中,AB=ED,∠B=∠CDE,BC=DC, △ABC≌△EDC.
点评:本考题题干简单清晰,但考点的内容与正多边形的知识相结合,需要具有分解基本图形的能力和基本的探究能力,才能顺利解题.二、紧扣三角形全等的判定,考查三角形全等的开放型问题.例3 (2008、丽水)如图,正方形ABCD中,E与F分别是AD、BC 上一点.在①AE=CF、②BE∥DF、③∠1 =∠2中,请选择其中一个条件,证明:BE=DF
(1)你选择的条件是 ▲ (只需填写序号);
(2)证明: 例1 (2008娄底)如图5,已知点D在△ABC的BC边上,DE∥AC交AB于E,DF ∥AB交AC于F.
(1)求证:AE=DF;
(2)若AD平分∠BAC,试判断四边形AEDF的形状,并说明理由.
分析:本题主要考查同学们对平行四边形及特殊的平行四边形的判定方法的把握.
证明:(1)∵ DE∥AC ,
∴∠ADE=∠DAF,同理∠DAE= ∠ FDA.
∵AD=DA,
∴△ADE≌△DAF,∴AE=DF.
(2)若AD平分∠BAC,四边形AEDF是菱形.
证明:∵ DE∥AC, DF ∥AB ,
∴四边形AEDF是平行四边形,
∵ ∠FAD= ∠ EAD,∴AF=DF,
∴平行四边形AEDF为菱形.
点评:三角形全等及平行四边形的性质都可以证明两线段相等,此类题起点低,注重基础知识及基本技能的考查,考查了同学们最基本的几何推理证明能力.§考点4:平行四边形、矩形、菱形、正方形、等腰梯形的性质与判定的考查。§考点5 取材于课本中的例、习题的变式试题拓展探究结论1:∠DOB=60°。
结论2:当AB,AC的夹角∠BAC不断变化时,EB,CD的夹角∠BOC保持不变,即∠BOC=120°不变。
结论3:若CD边上的高为AF,BE边上的高为AH,则AF=AH。
结论4:若CD边上的中线为AF,BE边上的中线为AH,AF=AH。
结论5:OA是∠DOE的平分线。
结论6:若∠BAC=60°,则①△AMN为等边三角形;②MN∥DE。例2 (08沈阳)已知:如图①所示,在 △ABC 和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,且点B,A,D在一条直线上,连接BE,CD,M,N分别为BE,CD的中点.
(1)求证:①BE=CD;②△AMN是等腰三角形.
(2)在图①的基础上,将△ADE绕点A按顺时针方向旋转 180°,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立;
(3)在(2)的条件下,请你在图②中延长ED交线段BC于点P.求证: △PBD ∽△AMN例3 (2008义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE。我们探究下列图中线段BG,线段DE的长度关系及所在的位置关系:
(1)①猜想如图1中线段BG,线段DE的长度关系及所在的位置关系;②将图1的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2、如图3情形。请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断例3 (2008义乌)如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连结BG,DE。我们探究下列图中线段BG,线段DE的长度关系及所在的位置关系:
(2)将原题中正方形改为矩形(如图4)且AB=a,BC=b, CE=ka, CG=kb(a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?以图5为例简要说明理由.本例还可以作如下操作变式探索:
连结AF,取AF的中点M,连结MD与MG。
① 探索线段MD与MG的数量关系。
② 设正方形ABCD的边长为b,正方形CEFG的边长为a(b≥2a),求△BFD的面积。§考题预测各位同仁多多指教!谢谢大家联系方式:13285782900 学校网址:www.zzjt.net
同课章节目录
