丽水市初中数学学业考试回顾与分析

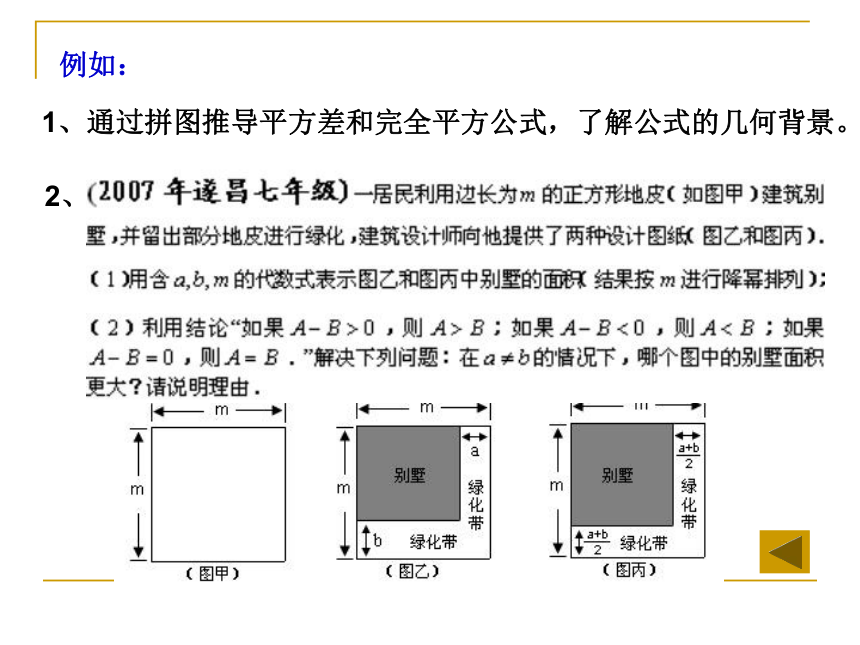
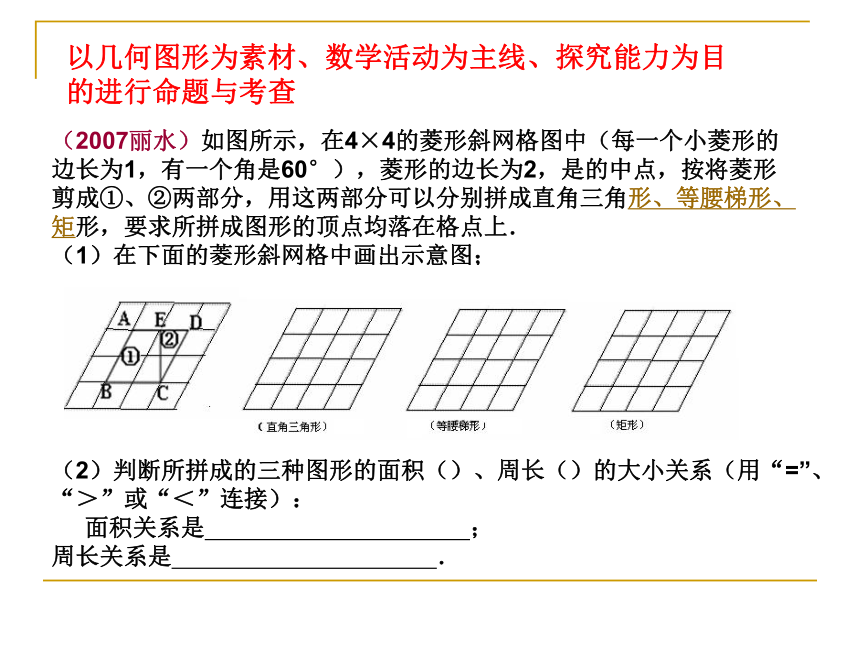
课件34张PPT。 丽水市初中数学学业考试 回顾与分析遂昌教研室 周顺利 2009年3月一、明确命题指导思想，整体把握教学要求二、2007、2008年我市学业考试试卷的整体特色三、基础性、发展性在试卷中的具体落实和体现四、值得同行们关注的三个方面内容提要一、明确命题指导思想，整体把握教学要求2、用好《考试说明》 2007、2008两年无论是试题内容，还是试卷结构都与《考试说明》一致，根据我市实际需要，2009年考试形式与时间稍作调整，但考试范围、考试要求始终还是与《考试说明》一致，具有很强复习指导意义。属于“初中毕业生学业考试”并非属于“各类高中招生文化考试”。主要是考查学业水平，适度强调选拔功能 ，2007、2008年考查基础知识和基本技能的试题占全卷分值的70%以上。1、领会《课标》精神 命题突出强调初中数学课程的基础性、普及性和发展性，着力于学习方式的改进和创新意识、实践能力的培养。基础性、普及性——决定了考试性质二、2007、2008年我市学业考试试卷的整体特色1、控制难度、降低起点、减缓坡度、突出基础性控制难度：前两年试卷难度控制在0.6——0.65左右降低起点，减缓坡度：填空题、选择题、解答题前面绝大部分的试题都是一个初中毕业生所需要掌握的基础知识和基本技能，真正体现“人人学必须的数学”。极力避免偏题、怪题的出现，部分试题源于教材，高于教材；例如2007年14题求梯子长度问题，2008年23题票区划分问题；望大家注重挖掘教材中典型的例习题。(一)、关于知识与技能的考查——突出基础性1、单独、直接考查基础的、重要的知识技能 单独、间接考查基础的、重要的知识技能三、基础性、发展性在试卷中的具体落实和体现2、核心内容重点考查3、新增(加强)内容要重视，删除内容不考查，减弱内容不拔高，高中内容不下放（2007丽水） 17．（本题8分）（2）解不等式：(2008丽水） 17．（本题8分）（2）因式分解： （1）计算：（1）计算：例1、请从下列三个代数式中任选两个构造一个分式，并化简该分式。例2、请你任选两个多项式进行加（或减）法运算，再将结果分解因式 题目活而不难，入口较宽，能体现思维的灵活性；同时给命题人员创设了更加丰富的命题形式，使试卷更加新颖活泼、生机活力。 初中数学的核心内容是学生今后进一步学习的基础，命题时强调核心内容的覆盖面，尽量突出对“数与式”、“方程与不等式”、“函数”、“基本图形的性质”、“图形间的基本关系”、“统计的应用” 、 “概率的计算” 等核心内容的考查。《数与代数》方面的变化加强的方面：1、强调通过实际情境使学生体验、感受和理解数与代数的意义。2、强调数学模型（方程、不等式、函数）减弱的方面：1、降低运算的复杂性、技巧和熟练程度的要求2、减少公式的条数，降低对记忆的要求——强调通性通法（1）数的计算（2）解方程：删除分式方程、根式方程、高次方程、二元二次方程组、三元一次方程组（相应二次函数的解析式）、一元二次方程中的判别式及韦达定理1、通过拼图推导平方差和完全平方公式，了解公式的几何背景。例如：2、《空间与图形》方面的变化加强的方面：1、强调内容的现实背景，联系学生的生活经验和活动经验2、增加了图形变换、位置的确定、视图与投影等内容3、加强了几何建模以及探究过程，强调几何直觉，培养空间观念4、加强合情推理，调整“证明”的要求，强化理性精神。减弱的方面：1、削弱了以演绎推理为主要形式的定理证明，减少定理的数量——用4条“基本事实”证明40条左右的结论；2、删去了大量繁难的几何证明题，淡化几何证明的技巧，降低了论证过程形式化的要求和证明的难度。以几何图形为素材、数学活动为主线、探究能力为目的进行命题与考查（2007丽水）如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形的边长为2，是的中点，按将菱形剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．
（1）在下面的菱形斜网格中画出示意图；（2）判断所拼成的三种图形的面积（）、周长（）的大小关系（用“=”、“＞”或“＜”连接）：
面积关系是 ；
周长关系是 ． （2008丽水）23．如图是2008北京奥运会某比赛场馆的平面图，根据距离比赛场地的远近和视角的不同，将观赛场地划分成A、B、C三个不同的票价区．其中与场地边缘的视角大于或等于45°，并且距场地边缘的距离不超过30米的区域划分为A票区，B票区如图所示，剩下的为C票区．
（1）请你利用尺规作图，在观赛场地中，作出票区所在的区域（只要求作出图形，保留作图痕迹，不要求写作法）；
（2）如果每个座位所占的平均面积是0.8平方米，请估算票区有多少个座位．23．如图是2008北京奥运会某比赛场馆的平面图，根据距离比赛场地的远近和视角的不同，将观赛场地划分成、、三个不同的票价区．其中与场地边缘的视角大于或等于45°，并且距场地边缘的距离不超过30米的区域划分为票区，票区如图所示，剩下的为票区．
（1）请你利用尺规作图，在观赛场地中，作出票区所在的区域（只要求作出图形，保留作图痕迹，不要求写作法）；
（2）如果每个座位所占的平均面积是0.8平方米，请估算票区有多少个座位．（第23题）《统计与概率》方面的变化（4）培养提取信息、统计、分析、决策能力强调与注意的方面： (1) 强调统计与概率过程性目标的达成 (2) 强调对统计表特征和统计量实际意义的理解 (3) 注意避免单纯的统计量的计算和对有关术语进行严格表述(二)、着力于学习能力的考查——强调发展性1、提取信息与资料处理的能力统计决策题、函数图象题2、语言表达能力3、解决问题的能力5、动手操作与探究能力4、应用建模能力作法、决策、推理论证6、知识整合运用能力课题学习关于作图问题三、例题剖析（2007丽水）如图所示，在4×4的菱形斜网格图中（每一个小菱形的边长为1，有一个角是60°），菱形的边长为2，是的中点，按将菱形剪成①、②两部分，用这两部分可以分别拼成直角三角形、等腰梯形、矩形，要求所拼成图形的顶点均落在格点上．
（1）在下面的菱形斜网格中画出示意图；（2）判断所拼成的三种图形的面积（）、周长（）的大小关系（用“=”、“＞”或“＜”连接）：
面积关系是 ；
周长关系是 ． （2008丽水）23．如图是2008北京奥运会某比赛场馆的平面图，根据距离比赛场地的远近和视角的不同，将观赛场地划分成A、B、C三个不同的票价区．其中与场地边缘的视角大于或等于45°，并且距场地边缘的距离不超过30米的区域划分为A票区，B票区如图所示，剩下的为C票区．
（1）请你利用尺规作图，在观赛场地中，作出票区所在的区域（只要求作出图形，保留作图痕迹，不要求写作法）；
（2）如果每个座位所占的平均面积是0.8平方米，请估算票区有多少个座位．23．如图是2008北京奥运会某比赛场馆的平面图，根据距离比赛场地的远近和视角的不同，将观赛场地划分成、、三个不同的票价区．其中与场地边缘的视角大于或等于45°，并且距场地边缘的距离不超过30米的区域划分为票区，票区如图所示，剩下的为票区．
（1）请你利用尺规作图，在观赛场地中，作出票区所在的区域（只要求作出图形，保留作图痕迹，不要求写作法）；
（2）如果每个座位所占的平均面积是0.8平方米，请估算票区有多少个座位．（第23题）(2007丽水)（本题8分）小明在复习数学知识时，针对“求一元二次方程的解”，整理了以下的几种方法，请你按有关内容补充完整：(2008丽水)22．为了加强视力保护意识，小明想在长为3.2米，宽为4.3米的书房里挂一张测试距离为5米的视力表．在一次课题学习课上，小明向全班同学征集“解决空间过小，如何放置视力表问题”的方案，其中甲、乙、丙三位同学设计方案新颖，构思巧妙．
（1）甲生的方案：如图1，将视力表挂在墙和墙的夹角处，被测试人站立在
对角线上，问：甲生的设计方案是否可行？请说明理由．
（2）乙生的方案：如图2，将视力表挂在墙上，在墙ABEF上挂一面足够大的平面镜，根据平面镜成像原理可计算得到：测试线应画在距离墙 ▲ 米处．
（3）丙生的方案：如图3，根据测试距离为5m的大视力表制作一个测试距离为3m的小视HH（图1）（图2）（图3）（第22题）3.5㎝ACF3mB5mD
力表．如果大视力表中“”的长是3.5cm，那么小视力表中相应“”的长是多少cm？ 四、值得同行们关注的几个方面（一）、全国各地正在尝试第四基的评价与考查（二）、当前命题突出对过程的考查（三）、进一步加强数学本质考查（一）、全国各地正在尝试第四基的评价与考查1、双基——三基——四基（即基础知识、基本技能、基本思想、基本活动经验）。2、什么是基本活动经验？（1）基本活动是指观察、操作（作图、拼图、折叠、剪纸、旋转等）、收集和处理信息、类比、归纳、猜想等活动（2）学生通过基本活动自己“发现”数学结论，这种自己“发现”的数学结论就是数学活动经验 。本题着重考查了观察、猜想、操作（拼图）、验证等活动过程性指标，有效评价了学生从事操作活动的经验与思维方式、图形的推理能力．如图，正方形卡片A类、B类和长方形卡片C类各若干张，如果要拼一个长为(a＋2b)、宽为(a＋b)的大长方形，则需要C类卡片 ▲ 张．3、例题欣赏（2008年湖北省咸宁市）如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．
实验与探究：
由图观察易知A（0，2）关于直线l的对称点的坐标为（2，0），请在图中分别标明B(5,3) 、C(-2,5) 关于直线l的对称点、的位置，并写出他们的坐标: 、 ；
归纳与发现：
结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P(a,b)关于第一、三象限的角平分线l的对称点的坐标为 （不必证明）；
运用与拓广：
已知两点D(1,-3)、E(-1,-4)，试在直线上确定一点Q，使点Q到D、E两点的距离之和最小，并求出Q点坐标．本题主要是以作图、观察、归纳等数学活动为载体获得基本数学活动经验（2008衢州）已知直角梯形纸片OABC在平面直角坐标系中的位置如图所示，四个顶点的坐标分别为O(0，0)，A(10，0)，B(8，)，C(0，)，点T在线段OA上(不与线段端点重合)，将纸片折叠，使点A落在射线AB上(记为点A′)，折痕经过点T，折痕TP与射线AB交于点P，设点T的横坐标为t，折叠后纸片重叠部分(图中的阴影部分)的面积为S；
(1)求∠OAB的度数，并求当点A′在线段AB上时，S关于t的函数关系式；
(2)当纸片重叠部分的图形是四边形时，求t的取值范围；
(3)S存在最大值吗？若存在，求出这个最大值，并求此时t的值；若不存在，请说明理由。
本题以折纸数学活动为载体考查学生基本数学活动经验（二）、当前命题突出对过程的考查 近几年来全国各地非常重视考查学生在数学活动过程中所表现出来的思维方式、思维水平，对活动对象、相关知识与方法的理解深度，从事探究与交流的意识。1、突出对数学活动过程的考查（2008丽水14.） 一元二次方程 可转化为两个一次方程，其中一个一次方程是 ，则另一个一次方程是 ▲ ． （2008金华19）、 在平面直角坐标系中，ΔABC的三个顶点的位置如图所示， 点A‵的坐标是(一2，2) ，现将，6.ABC平移。使点A变换为点A‵， 点B‵、C‵分别是B、C的对应点.
(1)请画出平移后的像Δ A‵ B‵C‵(不写画法) ，并直接写出点B‵、 C‵的坐标: B‵ ( )、C‵( )；
(2)若ΔABC内部一点P的坐标为（a，b） ，则点P的对应点p‵的 坐标是( )。（2008宁波26）．如图1，把一张标准纸一次又一次对开，得到“2开”纸、“4开”纸、“8开”纸、“16开”纸…．已知标准纸的短边长为a．
（1）如图2，把这张标准纸对开得到的“16开”张
纸按如下步骤折叠：
第一步 将矩形的短边AB与长边AD对齐折叠，
点B落在AD上的点B′处，铺平后得折痕AE；
第二步 将长边AD与折痕AE对齐折叠，点D
正好与点E重合，铺平后得折痕AF．则AD：AB
的值是 ，AD、AB的长分别是 ， ．
（2）“2开”纸、“4开”纸、“8开”纸的长与宽之比是否都相等？若相等，直接写出这个
比值；若不相等，请分别计算它们的比值．
（3）如图3，由8个大小相等的小正方形构成“L”型图案，它的四个顶点E、F、G、H。
分别在“16开”纸的边AB、BC、CD、DA上，求DG的长．
（4）已知梯形MNPQ中，MN∥PQ，∠M＝90°，MN＝MQ＝2PQ，且四个顶点M、N、P、ABCDBCADEGHFFE4开2开8开16开图1图2图3（第26题）a
Q都在“4开”纸的边上，请直接写出2个符合条件且大小不同的直角梯形的面积．2、如何对平常学习过程的评价学习习惯的养成、学习操作的流程、科学的学习方法等过程性因素如何评价？例题、请阅读下列解题过程，根据要求回答问题：问题（1）、本题所涉及到的数学知识主要有哪些？问题（2）、本题所蕴涵的数学思想主要是什么思想？问题（3）、本题求得AB=10这一结果解法很多，请你再写出一种解法。-----------------------------------------------------------------
-----------------------------------------------------------------
-----------------------------------------------------------------2008绍兴第23题值得学习和品味 这种考查方式有利于引导学生解题后进行及时的回顾总结、反思内化，久而久之便养成了总结反思的学习习惯，总结反思也是学生从事自主学习必不可少的科学方法之一，同时也是学习操作的流程之一。 这种考查方式也是对“例1讲了讲例2”教学现象的抨击，学生良好的学习习惯、规范的学习流程、科学的学习方法不是靠一时讲成的，而是在平常的教学过程中逐渐形成的。 例题教学后，引导学生归纳其中用到的知识、解决问题的思路和方法、解题的基本步骤和书写规范，有利于学生形成正确的解题策略；总结反思是例题教学的重要环节之一核心习题的教学应具备四个环节：习题的分析--------整体感知，形成思路习题的解答--------条理表达（板书、口述等方式）习题的总结--------总结反思，提升内化习题的迁移--------练习巩固，灵活运用知识教学过程（概念、定理、法则、公式）习题教学过程3、平常教学中值得关注的几个教学过程 总之，教师不仅要重视知识与技能的教学，也是重视学科思想的渗透，还要重视学习习惯的养成、学习方法的指导。为学生的后继学习和终生发展奠定良好的基础。（三）进一步加强数学本质考查进一步加强数学本质考查，追求内涵与形式之间的和谐与平衡 课改的大背景下，四处都着力于命题形式的创新，努力促进学习方式的改进，的确涌现出大批量的优秀试题，同时因过分追求形式的创新而淡化数学学科的本质，导致一些试题有形没质，缺乏数学味。（2008嘉兴第9题）如图，正方形中，是边上一点，以为圆心、为半径的半圆与以为圆心，为半径的圆弧外切，则的值为（ ）本题构图十分巧妙，表现在两个方面：有机的整合了正方形、圆、直角三角形、三角函数等方面的基础知识；高效考查了图形分解能力、观察能力，无声无息的渗透了方程思想。