重庆市开州区文峰教育集团2023-2024学年九年级下学期入学考试数学试卷(含答案)
文档属性
| 名称 | 重庆市开州区文峰教育集团2023-2024学年九年级下学期入学考试数学试卷(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 736.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-19 00:00:00 | ||
图片预览




文档简介
开州区文峰初中教育集团2024年春季九年级数学入学试题
(考试时间:120分钟 满分:150分)
注意事项:
1.试题的答案书写在答题卡上,不得在试题卷上直接作答;
2.作答前认真阅读答题卡上的注意事项;
3.作图(包括作辅助线)请一律用,黑色签字笔完成;
一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.
1.6的相反数是( )
A.﹣6 B. C. D.6
2.下列四个图形中,是中心对称图形的是( )
A. B. C. D.
3.下列各点中,在反比例函数y=的图象上的是( )
A.(﹣1,4) B.(1,4) C.(1,﹣4) D.(2,3)
4.若两个相似三角形的周长之比是1:2,则它们的面积之比是( )
A.1:2 B.1: C.1:4 D.2:1
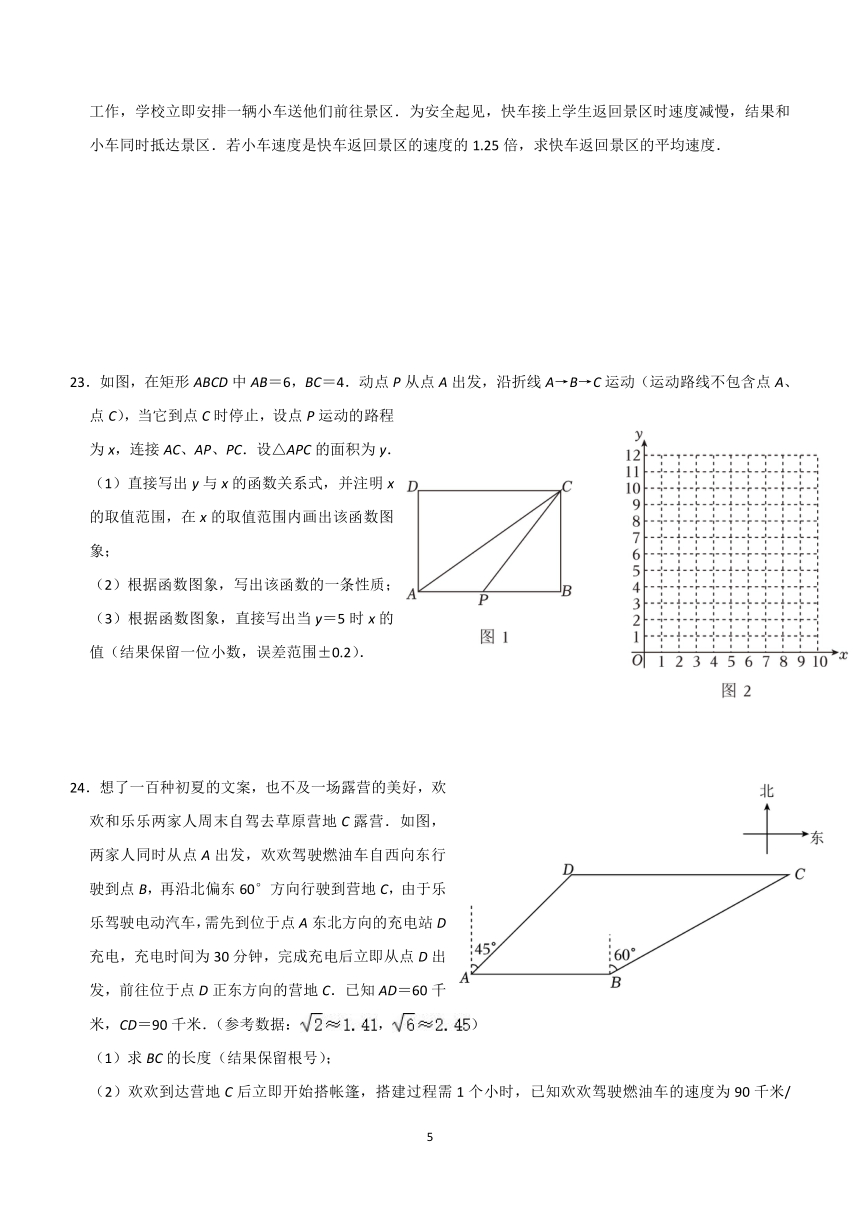
5.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
第5题图 第8题图 第9题图
6.估计的值应在( )
A.5和6之间 B.2和3之间 C.3和4之间 D.4和5之间
7.观察下列四个图形组成的一组图形,发现它们是按照一定规律排列的,依此规律排列下去,第10个图形共有( )个点组成.
A.26 B.27 C.28 D.29.
8.如图,PM与⊙O相切于点M,OP=4,∠OPM=30°,则OM长为( )
A.2 B.4 C.4 D.
9.如图,已知正方形ABCD的边长为3,点P是对角线BD上的一点,PF⊥AD于点F,PE⊥AB于点E,连接PC,当PE:PF=1:2时,则PC=( )
A. B.2 C. D.
10. 已知关于的两个多项式,.其中a为常数,下列说法:
①若的值始终与无关,则;
②关于x的方程始终有两个不相等的实数根;
③若的结果不含的项,则;
④当时,若的值为整数,则x的整数值只有2个.
以上结论正确的个数有( )
A. 4 B. 3 C. 2 D. 1
二、填空题:(本大题8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡中对应的横线上.
11.2﹣1+20230= .
12.若一个多边形的内角和比外角和大360°,则这个多边形的边数为 .
13.将分别标有数字1,2,3的三个小球放入一个不透明的袋子中,这些小球除数字外其他都相同.从中随机摸出一个小球记下数字后放回,再从中随机摸出一个小球并记下数字,则两次摸出的小球数字相同的概率 .
14.某校截止到2022年底,校园绿化面积为800平方米.为美化环境,该校计划2024年底绿化面积达到1240平方米.利用方程思想,设这两年绿化面积的年平均增长率为x,则依题意列方程为 .
15.如图,矩形ABCD中,AB=3,AD=.以A为圆心,AD为半径作弧交BC于点E,则图中阴影部分的面积为 .
第15题 第16题
16.如图,在等腰三角形纸片ABC中,AB=AC,∠A=40°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= °.
17.若关于x的不等式组有且仅有四个整数解,关于y的分式方程+=1有整数解,则符合条件的所有整数a的和是 .
18.若一个三位正整数m=(各个数位上的数字均不为0)满足a+b+c=9,则称这个三位正整数为“吉祥数”.对于一个“吉祥数”m,将它的百位数字和个位数字交换以后得到新数n,记F(m)=.如:m=216满足2+1+6=9,则216为“吉祥数”,那么n=612,所以F(216)==92.则最小的“吉祥数”是 ;对于任意一个“吉祥数”m,若F(m)能被7整除,则满足条件的“吉祥数”m的最大值是 .
三、解答题:(本大题8个小题,第19题8分,其余每题各10分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
19.计算:(1)(a﹣2)2+(1+a)(1﹣a); (2)(m+2﹣)÷
20.如图,在△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°能与△DEC重合.
(1)请用尺规作图法,作AC的垂直平分线,垂足为F;(不要求写作法,保留作图痕迹)
(2)在(1)问情况下,连接DF,求证:△CFD≌△ABC(填空).
证明:(2)∵点F是边AC中点,∴CF=① ,
∵∠BCA=30°,∠ABC=90°,∴,∴AB=② ,
∵将△ABC绕点C顺时针旋转60°得到△DEC,∴AC=CD,∠FCD=60°,
∴∠A=③ ,
在△ABC和△CFD中, ∴△ABC≌△CFD(SAS).
21.“感受数学魅力,提升数学素养”,某校在其举办的数学文化节上开展了趣味数学知识竞赛,现从七年级和八年级参与竞赛的学生中各随机抽取10名同学的成绩进行整理、描述和分析(单位:分,满分100分,90分及90分以上为优秀),将学生竞赛成绩分为A,B,C三个等级:
A:70≤x<80,B:80≤x<90,C:90≤x≤100.下面给出了部分信息:
七年级10名学生的竞赛成绩为:74,75,84,84,84,86,86,95,95,97;
八年级10名学生的竞赛成绩在B等级中的数据为:81,82,84,88,88.
两组数据的平均数、中位数、众数如下表所示:
学生 平均数 中位数 众数
七年级 86 85 b
八年级 86 a 88
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,m= ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由(一条理由即可);
(3)若八年级共有500名学生参赛,估计八年级参赛学生中成绩为优秀的人数.
22.八年级学生到距学校150km的景区游览.景区提供了快车和慢车两种车型前往学校接学生到景区,所有车辆均沿同一路线往返.
(1)由于快车有其他接送任务,八年级(1)班学生乘慢车从学校出发时,快车才从景区出发前往学校接八年级(2)班学生,1.2小时后快车在前往学校的途中与慢车相遇.若快车每小时比慢车多行驶25km,求慢车的平均速度;
(2)有四名学生负责准备活动道具,在八年级(2)班学生乘快车出发0.5小时后,他们四人才完成准备工作,学校立即安排一辆小车送他们前往景区.为安全起见,快车接上学生返回景区时速度减慢,结果和小车同时抵达景区.若小车速度是快车返回景区的速度的1.25倍,求快车返回景区的平均速度.
23.如图,在矩形ABCD中AB=6,BC=4.动点P从点A出发,沿折线A→B→C运动(运动路线不包含点A、点C),当它到点C时停止,设点P运动的路程为x,连接AC、AP、PC.设△APC的面积为y.
(1)直接写出y与x的函数关系式,并注明x的取值范围,在x的取值范围内画出该函数图象;
(2)根据函数图象,写出该函数的一条性质;
(3)根据函数图象,直接写出当y=5时x的值(结果保留一位小数,误差范围±0.2).
24.想了一百种初夏的文案,也不及一场露营的美好,欢欢和乐乐两家人周末自驾去草原营地C露营.如图,两家人同时从点A出发,欢欢驾驶燃油车自西向东行驶到点B,再沿北偏东60°方向行驶到营地C,由于乐乐驾驶电动汽车,需先到位于点A东北方向的充电站D充电,充电时间为30分钟,完成充电后立即从点D出发,前往位于点D正东方向的营地C.已知AD=60千米,CD=90千米.(参考数据:,)
(1)求BC的长度(结果保留根号);
(2)欢欢到达营地C后立即开始搭帐篷,搭建过程需1个小时,已知欢欢驾驶燃油车的速度为90千米/时,乐乐驾驶电动汽车的速度为75千米/时,请计算说明欢欢能否在乐乐到达营地C前搭完帐篷.
25.如图,在平面直角坐标系中,抛物线y=ax2﹣x+c(a≠0)与x轴交于A(﹣1,0)、B(3,0)两点,直线AC与y轴交于点C,与抛物线交于点D,OA=OC.
(1)求该抛物线与直线AC的解析式;
(2)若点E是x轴下方抛物线上一动点,连接AE、CE.求△ACE面积的最大值及此时点E的坐标;
(3)将原抛物线沿射线AD方向平移2个单位长度,得到新抛物线:y1=a1x2+b1x+c1(a≠0),新抛物线与原抛物线交于点F,在直线AD上是否存在点P,使以点P、D、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
26.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,连接AD,若CE=2,BD=3,∠C=45°,求△ADE的面积;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,若∠C=30°,将△BCE沿BE折叠,得到△BEF,且BF与AC交于点G,连接AD,DF,点E在AC边上运动的过程中,当BF⊥AC时,直接写出的值.
开州区文峰初中教育集团2024年春季九年级数学入学试题答案
一.选择题:
1-5:A D B C C 6-10:A C A D B
10.【解答】解:①∵A=x2﹣ax﹣2,B=x2﹣2x﹣3,
∴A﹣B=(x2﹣ax﹣2)﹣(x2﹣2x﹣3)=(2﹣a)x+1,∵A﹣B的值始终与x无关,
∴a=2,故①不符合题意;
②A+B=x2﹣ax﹣2+x2﹣2x﹣3=2x2﹣(a+2)x﹣5=0,∵Δ=(a+2)2+40>0,
∴关于x的方程A+B=0始终有两个不相等的实数根,故②符合题意;
③A B=(x2﹣ax﹣2) (x2﹣2x﹣3)=x4﹣(2+a)x3+(2a,﹣5)x2+(3a+4)x+6,
∵A B的结果不含x2的项,∴2a﹣5=0,解得a=;故③符合题意;
④当a=1时,A=x2﹣x﹣2,∴====1+,
∵的值为整数,∴x﹣3=±1,解得x=4或x=2,故④符合题意;
故选:B.
二.填空题
11. 1.5 12. 6 13. 14.
15. 16. 30 17. ﹣10 18. 117 351
17.【解答】解:关于x的不等式组整理得,∵关于x的不等式组有且仅有四个整数解,
∴1≤<2,∴﹣8<a≤﹣3,解分式方程得y=且≠2,
∵关于y的分式方程有整数解,且a为整数,∴符合条件的所有整数a为﹣7,﹣3,
∴符合条件的所有整数a的和为:﹣7﹣3=﹣10.
故答案为:﹣10.
18.【解答】解:(1)∵a+b+c=9,各个数位上的数字均不为0,这个三位数要最小,
∴百位上是1,十位上是1,∴个位是7,∴最小的“吉祥数”是 117;
(2)设m=100a+10b+c,其中a+b+c=9,则n=100c+10b+a,
∴F(m)=====101﹣9b,
∵a+b+c=9,且a,b,c均不为0,∴b=1,2,3......7,
∴a+c=4,∴,,,
∴m=153或252或351,∴满足条件的“吉祥数”m的最大值是315.
三.解答题
19.计算:(1)(a﹣2)2+(1+a)(1﹣a);(2)(m+2﹣)÷.
【解答】解:(1)原式=a2+4﹣4a+1﹣a2=5﹣4a;
(2)原式=(﹣) = =﹣.
20.【解答】(1)解:
(2),CF,∠FCD,AC=CD.
21.(1)填空:a= 86 ,b= 84 ,m= 30 ;
【解答】解:(1)由扇形统计图可得,八年级A等级的有10×20%=2(人),
把八年级10名同学的成绩从小到大排列,排在中间的数分别是84,88,故中位数a==86;
在74,75,84,84,84,86,86,95,95,97中,出现次数最多的是84,
∴众数b=84;m%=1﹣20%﹣=30%,即m=30,
(2)八年级的成绩更好,理由如下:因为八年级竞赛成绩众数88大于七年级竞赛成绩众数84;
(3)500×30%=150(名),答:估计八年级参赛学生中成绩为优秀的人数为150名.
声明:试题解析著作权属所有,未22.解:(1)设慢车的平均速度为x km/h,则快车的平均速度为(x+25)km/h,
根据题意得:1.2x+1.2(x+25)=150,解得:x=50.答:慢车的平均速度为50km/h;
(2)设快车返回景区的平均速度为y km/h,则小车的平均速度为1.25y km/h,
根据题意得:﹣=0.5,解得:y=60,经检验,y=60是所列方程的解,且符合题意.
答:快车返回景区的平均速度为60km/h.
23.解:(1)
在x的取值范围内画出y的函数图象如图.
(2)根据图象可知:当0(3)x=2.5或8.3
24.解:(1)过点A作AE⊥CD交CD延长线于点E,过点B作BF⊥CD于点F,
由题意知,AB∥CD,∴四边形ABFE是矩形,
∴AE=BF,AB=EF,
在Rt△ADE中,∵∠DAE=45°,AD=60千米,
cos∠DAE=,∴AE=AD cos∠DAE=60 cos45°=(千米),∴BF=千米,
在Rt△BCF中,∵BF=千米,∠CBF=60°,cos∠CBF=,
∴BC=(千米),
答:BC的长度为千米.
(2)在Rt△ADE中,∵∠DAE=45°,∴∠ADE=45°,
∴DE=AE=≈42.3(千米),
在Rt△BCF中,∵BF=千米,∠CBF=60°,
tan∠CBF=,cos∠CBF=,
∴CF=BF tan∠CBF= tan60°=≈73.5(千米),
BC===≈84.6(千米),
∴AB=EF=ED+CD﹣CF≈42.3+90﹣73.5=58.8(千米),
∴欢欢家从点A出发到点C所走的路程为:AB+BC=58.5+84.6=143.1(千米),
所用时间为:=1.59(小时),
乐乐从点A出发到点C所走的路程为:AD+DC=60+90=150(千米),
所用时间为:=2.5(小时),∵2.5﹣1.59=0.91<1,
∴欢欢不能在乐乐到达营地C前搭完帐篷.
25.如图,在平面直角坐标系中,抛物线y=ax2﹣x+c(a≠0)与x轴交于A(﹣1,0)、B(3,0)两点,直线AC与y轴交于点C,与抛物线交于点D,OA=OC.
(1)求该抛物线与直线AC的解析式;
(2)若点E是x轴下方抛物线上一动点,连接AE、CE.求△ACE面积的最大值及此时点E的坐标;
(3)将原抛物线沿射线AD方向平移2个单位长度,得到新抛物线:y1=a1x2+b1x+c1(a≠0),新抛物线与原抛物线交于点F,在直线AD上是否存在点P,使以点P、D、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.x1
【解答】解:(1)把A(﹣1,0)、B(3,0)代入y=ax2﹣x+c,得,解得,
∴抛物线的解析式为y=x2﹣x﹣;∵OC=OA=1,∴C(0,1),
设直线AC的解析式为y=kx+1,则﹣k+1=0,解得k=1,∴直线AC的解析式为y=x+1.
(2)如图1,作EG⊥x轴交直线AC于点G,作EH⊥AD于点H.
设E(x,x2﹣x﹣)(﹣1<x<3),则G(x,x+1),∴EG=x+1﹣(x2﹣x﹣)=x2+2x+.
∵OA=OC=1,∠AOC=90°,∴∠OCA=45°,AC==,
∵∠HGE=∠OCA=45°,∴EH=EG sin45°=(x2+2x+),
∴S△ACE=××(x2+2x+)=x2+x+=(x﹣2)2+,
∵<0,且﹣1<2<3,∴当x=2时,S△ACE最大=,此时E(2,).
∴△ACE面积的最大值为,此时点E的坐标为(2,).
(3)存在.如图2,在直线AC上取一点A′,使它的横坐标为1,则A′(1,2),AA′==2,
∴点A′即为抛物线平移后点A的对应点,可知抛物线向右、向上各平移2个单位长度.
∵y=x2﹣x﹣=(x﹣1)2﹣2,∴平移后的抛物线为y=(x﹣3)2,其顶点坐标为(3,0);
∵原抛物线与新抛物线都经过点B(3,0),∴点B即为新抛物线与原抛物线的交点F.
作A′K⊥x轴于点K,则∠AKA′=∠FKA′=90°,AK=A′K=FK=2,
∴∠AA′K=∠FA′K=45°,∴∠AA′F=90°.由,得或(不符合题意,舍去),∴D(5,6),∴FD==2.
①当FP1=FD时,则点P1与点D关于点A′对称,∴P1(﹣3,﹣2);
②当P2D=FD=2时,∵CD=×5=5,∴CP2=5﹣2,
∴xp=×(5﹣2)=5,yp=5+1=6,P2(5,6);
③当DP3=FP3时,∵∠P3DF=∠FDP1,∠DFP3=∠DP1F,∴△P3DF∽△FDP1,
∴,∵DP1=×(5+3)=8,∴P3D===,
∴CP3=﹣=,∴xp=×=,yp==,∴P3(,);
④当P4D=FD=时,则CP4=+,
∴xp=×(+)=5+2,yp=5+2+1=6+2,
∴P4(5+,6+).
综上所述,点P的坐标为(﹣3,﹣2)或(5,6)或(,)或(5+,6+).
26.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,连接AD,若CE=2,BD=3,∠C=45°,求△ADE的面积;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,若∠C=30°,将△BCE沿BE折叠,得到△BEF,且BF与AC交于点G,连接AD,DF,点E在AC边上运动的过程中,当BF⊥AC时,直接写出的值.
【解答】(1)解:∵ED⊥AC,∠C=45°,∴∠EDC=∠C=45°,∴CE=DE=2,
∴,∵,∴,
在直角△ABC中,∠ABC=90°,∠C=45°,∴∠BAC=∠C=45°,∴,
∴,∴AE=AC﹣CE=8,;
(2)证明:如图2中,过点B作BT⊥BE交ED的延长线于点T.
∵∠BDE=∠CDF,∴∠CDE=∠BDF,∵DE⊥AC,
∴∠DEC=∠ABC=90°,∴∠A+∠C=∠EDC+∠C=90°,
∴∠EDC=∠A,∴∠A=∠BDF,∵∠ABF=∠DBF,BF=BF,
∴△ABF≌△DBF(SAS),∴AB=BD,∵∠ABC=∠EBT=90°,
∴∠ABE=∠DBT,∵∠BDT=∠CDE=∠A,∴△ABE≌△DBT(ASA),
∴BE=BT,AE=DT,∴AE+DE=DT+DE=ET,
∴△BET是等腰直角三角形,∴,∴;
(3)解:如图,
∵∠C=30°,∴∠BAC=60°,当BF⊥AC时,∠ABG=30°,
∵将△BCE沿BE折叠,得到△BEF,∴∠FBE=∠CBE=30°,
又∠C=∠EBC=30°,∴EB=EC,EB=EA,
∴△ABE是等边三角形,设AB=a,则AC=2a,
∴,∴BF=2BG=2×GE=AE=a,
∵BD=a,在Rt△ABD中,AD=2BD=a,如图,连接AF,
∵GE⊥BF,EF=EB,
∴∠AEF=∠AEB=60°,
∴△AFE是等边三角形,
∴AF=AE=AB,
∴∠FAD=∠FAE+∠EAD=60°+30°=90°,
∴DF===,
∴==.
(考试时间:120分钟 满分:150分)
注意事项:
1.试题的答案书写在答题卡上,不得在试题卷上直接作答;
2.作答前认真阅读答题卡上的注意事项;
3.作图(包括作辅助线)请一律用,黑色签字笔完成;
一、选择题:(本大题10个小题,每小题4分,共40分)在每个小题的下面,都给出了代号为A、B、C、D的四个答案,其中只有一个是正确的,请将答题卡上题号右侧正确答案所对应的方框涂黑.
1.6的相反数是( )
A.﹣6 B. C. D.6
2.下列四个图形中,是中心对称图形的是( )
A. B. C. D.
3.下列各点中,在反比例函数y=的图象上的是( )
A.(﹣1,4) B.(1,4) C.(1,﹣4) D.(2,3)
4.若两个相似三角形的周长之比是1:2,则它们的面积之比是( )
A.1:2 B.1: C.1:4 D.2:1
5.如图,AB∥CD,FE⊥DB,垂足为E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
第5题图 第8题图 第9题图
6.估计的值应在( )
A.5和6之间 B.2和3之间 C.3和4之间 D.4和5之间
7.观察下列四个图形组成的一组图形,发现它们是按照一定规律排列的,依此规律排列下去,第10个图形共有( )个点组成.
A.26 B.27 C.28 D.29.
8.如图,PM与⊙O相切于点M,OP=4,∠OPM=30°,则OM长为( )
A.2 B.4 C.4 D.
9.如图,已知正方形ABCD的边长为3,点P是对角线BD上的一点,PF⊥AD于点F,PE⊥AB于点E,连接PC,当PE:PF=1:2时,则PC=( )
A. B.2 C. D.
10. 已知关于的两个多项式,.其中a为常数,下列说法:
①若的值始终与无关,则;
②关于x的方程始终有两个不相等的实数根;
③若的结果不含的项,则;
④当时,若的值为整数,则x的整数值只有2个.
以上结论正确的个数有( )
A. 4 B. 3 C. 2 D. 1
二、填空题:(本大题8个小题,每小题4分,共32分)请将每小题的答案直接填在答题卡中对应的横线上.
11.2﹣1+20230= .
12.若一个多边形的内角和比外角和大360°,则这个多边形的边数为 .
13.将分别标有数字1,2,3的三个小球放入一个不透明的袋子中,这些小球除数字外其他都相同.从中随机摸出一个小球记下数字后放回,再从中随机摸出一个小球并记下数字,则两次摸出的小球数字相同的概率 .
14.某校截止到2022年底,校园绿化面积为800平方米.为美化环境,该校计划2024年底绿化面积达到1240平方米.利用方程思想,设这两年绿化面积的年平均增长率为x,则依题意列方程为 .
15.如图,矩形ABCD中,AB=3,AD=.以A为圆心,AD为半径作弧交BC于点E,则图中阴影部分的面积为 .
第15题 第16题
16.如图,在等腰三角形纸片ABC中,AB=AC,∠A=40°,折叠该纸片,使点A落在点B处,折痕为DE,则∠CBE= °.
17.若关于x的不等式组有且仅有四个整数解,关于y的分式方程+=1有整数解,则符合条件的所有整数a的和是 .
18.若一个三位正整数m=(各个数位上的数字均不为0)满足a+b+c=9,则称这个三位正整数为“吉祥数”.对于一个“吉祥数”m,将它的百位数字和个位数字交换以后得到新数n,记F(m)=.如:m=216满足2+1+6=9,则216为“吉祥数”,那么n=612,所以F(216)==92.则最小的“吉祥数”是 ;对于任意一个“吉祥数”m,若F(m)能被7整除,则满足条件的“吉祥数”m的最大值是 .
三、解答题:(本大题8个小题,第19题8分,其余每题各10分,共78分)解答时每小题必须给出必要的演算过程或推理步骤,画出必要的图形(包括辅助线),请将解答过程书写在答题卡中对应的位置上.
19.计算:(1)(a﹣2)2+(1+a)(1﹣a); (2)(m+2﹣)÷
20.如图,在△ABC中,∠ABC=90°,∠ACB=30°,将△ABC绕点C顺时针旋转60°能与△DEC重合.
(1)请用尺规作图法,作AC的垂直平分线,垂足为F;(不要求写作法,保留作图痕迹)
(2)在(1)问情况下,连接DF,求证:△CFD≌△ABC(填空).
证明:(2)∵点F是边AC中点,∴CF=① ,
∵∠BCA=30°,∠ABC=90°,∴,∴AB=② ,
∵将△ABC绕点C顺时针旋转60°得到△DEC,∴AC=CD,∠FCD=60°,
∴∠A=③ ,
在△ABC和△CFD中, ∴△ABC≌△CFD(SAS).
21.“感受数学魅力,提升数学素养”,某校在其举办的数学文化节上开展了趣味数学知识竞赛,现从七年级和八年级参与竞赛的学生中各随机抽取10名同学的成绩进行整理、描述和分析(单位:分,满分100分,90分及90分以上为优秀),将学生竞赛成绩分为A,B,C三个等级:
A:70≤x<80,B:80≤x<90,C:90≤x≤100.下面给出了部分信息:
七年级10名学生的竞赛成绩为:74,75,84,84,84,86,86,95,95,97;
八年级10名学生的竞赛成绩在B等级中的数据为:81,82,84,88,88.
两组数据的平均数、中位数、众数如下表所示:
学生 平均数 中位数 众数
七年级 86 85 b
八年级 86 a 88
根据以上信息,解答下列问题:
(1)填空:a= ,b= ,m= ;
(2)根据以上数据,你认为在此次知识竞赛中,哪个年级的成绩更好?请说明理由(一条理由即可);
(3)若八年级共有500名学生参赛,估计八年级参赛学生中成绩为优秀的人数.
22.八年级学生到距学校150km的景区游览.景区提供了快车和慢车两种车型前往学校接学生到景区,所有车辆均沿同一路线往返.
(1)由于快车有其他接送任务,八年级(1)班学生乘慢车从学校出发时,快车才从景区出发前往学校接八年级(2)班学生,1.2小时后快车在前往学校的途中与慢车相遇.若快车每小时比慢车多行驶25km,求慢车的平均速度;
(2)有四名学生负责准备活动道具,在八年级(2)班学生乘快车出发0.5小时后,他们四人才完成准备工作,学校立即安排一辆小车送他们前往景区.为安全起见,快车接上学生返回景区时速度减慢,结果和小车同时抵达景区.若小车速度是快车返回景区的速度的1.25倍,求快车返回景区的平均速度.
23.如图,在矩形ABCD中AB=6,BC=4.动点P从点A出发,沿折线A→B→C运动(运动路线不包含点A、点C),当它到点C时停止,设点P运动的路程为x,连接AC、AP、PC.设△APC的面积为y.
(1)直接写出y与x的函数关系式,并注明x的取值范围,在x的取值范围内画出该函数图象;
(2)根据函数图象,写出该函数的一条性质;
(3)根据函数图象,直接写出当y=5时x的值(结果保留一位小数,误差范围±0.2).
24.想了一百种初夏的文案,也不及一场露营的美好,欢欢和乐乐两家人周末自驾去草原营地C露营.如图,两家人同时从点A出发,欢欢驾驶燃油车自西向东行驶到点B,再沿北偏东60°方向行驶到营地C,由于乐乐驾驶电动汽车,需先到位于点A东北方向的充电站D充电,充电时间为30分钟,完成充电后立即从点D出发,前往位于点D正东方向的营地C.已知AD=60千米,CD=90千米.(参考数据:,)
(1)求BC的长度(结果保留根号);
(2)欢欢到达营地C后立即开始搭帐篷,搭建过程需1个小时,已知欢欢驾驶燃油车的速度为90千米/时,乐乐驾驶电动汽车的速度为75千米/时,请计算说明欢欢能否在乐乐到达营地C前搭完帐篷.
25.如图,在平面直角坐标系中,抛物线y=ax2﹣x+c(a≠0)与x轴交于A(﹣1,0)、B(3,0)两点,直线AC与y轴交于点C,与抛物线交于点D,OA=OC.
(1)求该抛物线与直线AC的解析式;
(2)若点E是x轴下方抛物线上一动点,连接AE、CE.求△ACE面积的最大值及此时点E的坐标;
(3)将原抛物线沿射线AD方向平移2个单位长度,得到新抛物线:y1=a1x2+b1x+c1(a≠0),新抛物线与原抛物线交于点F,在直线AD上是否存在点P,使以点P、D、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.
26.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,连接AD,若CE=2,BD=3,∠C=45°,求△ADE的面积;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,若∠C=30°,将△BCE沿BE折叠,得到△BEF,且BF与AC交于点G,连接AD,DF,点E在AC边上运动的过程中,当BF⊥AC时,直接写出的值.
开州区文峰初中教育集团2024年春季九年级数学入学试题答案
一.选择题:
1-5:A D B C C 6-10:A C A D B
10.【解答】解:①∵A=x2﹣ax﹣2,B=x2﹣2x﹣3,
∴A﹣B=(x2﹣ax﹣2)﹣(x2﹣2x﹣3)=(2﹣a)x+1,∵A﹣B的值始终与x无关,
∴a=2,故①不符合题意;
②A+B=x2﹣ax﹣2+x2﹣2x﹣3=2x2﹣(a+2)x﹣5=0,∵Δ=(a+2)2+40>0,
∴关于x的方程A+B=0始终有两个不相等的实数根,故②符合题意;
③A B=(x2﹣ax﹣2) (x2﹣2x﹣3)=x4﹣(2+a)x3+(2a,﹣5)x2+(3a+4)x+6,
∵A B的结果不含x2的项,∴2a﹣5=0,解得a=;故③符合题意;
④当a=1时,A=x2﹣x﹣2,∴====1+,
∵的值为整数,∴x﹣3=±1,解得x=4或x=2,故④符合题意;
故选:B.
二.填空题
11. 1.5 12. 6 13. 14.
15. 16. 30 17. ﹣10 18. 117 351
17.【解答】解:关于x的不等式组整理得,∵关于x的不等式组有且仅有四个整数解,
∴1≤<2,∴﹣8<a≤﹣3,解分式方程得y=且≠2,
∵关于y的分式方程有整数解,且a为整数,∴符合条件的所有整数a为﹣7,﹣3,
∴符合条件的所有整数a的和为:﹣7﹣3=﹣10.
故答案为:﹣10.
18.【解答】解:(1)∵a+b+c=9,各个数位上的数字均不为0,这个三位数要最小,
∴百位上是1,十位上是1,∴个位是7,∴最小的“吉祥数”是 117;
(2)设m=100a+10b+c,其中a+b+c=9,则n=100c+10b+a,
∴F(m)=====101﹣9b,
∵a+b+c=9,且a,b,c均不为0,∴b=1,2,3......7,
∴a+c=4,∴,,,
∴m=153或252或351,∴满足条件的“吉祥数”m的最大值是315.
三.解答题
19.计算:(1)(a﹣2)2+(1+a)(1﹣a);(2)(m+2﹣)÷.
【解答】解:(1)原式=a2+4﹣4a+1﹣a2=5﹣4a;
(2)原式=(﹣) = =﹣.
20.【解答】(1)解:
(2),CF,∠FCD,AC=CD.
21.(1)填空:a= 86 ,b= 84 ,m= 30 ;
【解答】解:(1)由扇形统计图可得,八年级A等级的有10×20%=2(人),
把八年级10名同学的成绩从小到大排列,排在中间的数分别是84,88,故中位数a==86;
在74,75,84,84,84,86,86,95,95,97中,出现次数最多的是84,
∴众数b=84;m%=1﹣20%﹣=30%,即m=30,
(2)八年级的成绩更好,理由如下:因为八年级竞赛成绩众数88大于七年级竞赛成绩众数84;
(3)500×30%=150(名),答:估计八年级参赛学生中成绩为优秀的人数为150名.
声明:试题解析著作权属所有,未22.解:(1)设慢车的平均速度为x km/h,则快车的平均速度为(x+25)km/h,
根据题意得:1.2x+1.2(x+25)=150,解得:x=50.答:慢车的平均速度为50km/h;
(2)设快车返回景区的平均速度为y km/h,则小车的平均速度为1.25y km/h,
根据题意得:﹣=0.5,解得:y=60,经检验,y=60是所列方程的解,且符合题意.
答:快车返回景区的平均速度为60km/h.
23.解:(1)
在x的取值范围内画出y的函数图象如图.
(2)根据图象可知:当0
24.解:(1)过点A作AE⊥CD交CD延长线于点E,过点B作BF⊥CD于点F,
由题意知,AB∥CD,∴四边形ABFE是矩形,
∴AE=BF,AB=EF,
在Rt△ADE中,∵∠DAE=45°,AD=60千米,
cos∠DAE=,∴AE=AD cos∠DAE=60 cos45°=(千米),∴BF=千米,
在Rt△BCF中,∵BF=千米,∠CBF=60°,cos∠CBF=,
∴BC=(千米),
答:BC的长度为千米.
(2)在Rt△ADE中,∵∠DAE=45°,∴∠ADE=45°,
∴DE=AE=≈42.3(千米),
在Rt△BCF中,∵BF=千米,∠CBF=60°,
tan∠CBF=,cos∠CBF=,
∴CF=BF tan∠CBF= tan60°=≈73.5(千米),
BC===≈84.6(千米),
∴AB=EF=ED+CD﹣CF≈42.3+90﹣73.5=58.8(千米),
∴欢欢家从点A出发到点C所走的路程为:AB+BC=58.5+84.6=143.1(千米),
所用时间为:=1.59(小时),
乐乐从点A出发到点C所走的路程为:AD+DC=60+90=150(千米),
所用时间为:=2.5(小时),∵2.5﹣1.59=0.91<1,
∴欢欢不能在乐乐到达营地C前搭完帐篷.
25.如图,在平面直角坐标系中,抛物线y=ax2﹣x+c(a≠0)与x轴交于A(﹣1,0)、B(3,0)两点,直线AC与y轴交于点C,与抛物线交于点D,OA=OC.
(1)求该抛物线与直线AC的解析式;
(2)若点E是x轴下方抛物线上一动点,连接AE、CE.求△ACE面积的最大值及此时点E的坐标;
(3)将原抛物线沿射线AD方向平移2个单位长度,得到新抛物线:y1=a1x2+b1x+c1(a≠0),新抛物线与原抛物线交于点F,在直线AD上是否存在点P,使以点P、D、F为顶点的三角形是等腰三角形?若存在,直接写出点P的坐标;若不存在,请说明理由.x1
【解答】解:(1)把A(﹣1,0)、B(3,0)代入y=ax2﹣x+c,得,解得,
∴抛物线的解析式为y=x2﹣x﹣;∵OC=OA=1,∴C(0,1),
设直线AC的解析式为y=kx+1,则﹣k+1=0,解得k=1,∴直线AC的解析式为y=x+1.
(2)如图1,作EG⊥x轴交直线AC于点G,作EH⊥AD于点H.
设E(x,x2﹣x﹣)(﹣1<x<3),则G(x,x+1),∴EG=x+1﹣(x2﹣x﹣)=x2+2x+.
∵OA=OC=1,∠AOC=90°,∴∠OCA=45°,AC==,
∵∠HGE=∠OCA=45°,∴EH=EG sin45°=(x2+2x+),
∴S△ACE=××(x2+2x+)=x2+x+=(x﹣2)2+,
∵<0,且﹣1<2<3,∴当x=2时,S△ACE最大=,此时E(2,).
∴△ACE面积的最大值为,此时点E的坐标为(2,).
(3)存在.如图2,在直线AC上取一点A′,使它的横坐标为1,则A′(1,2),AA′==2,
∴点A′即为抛物线平移后点A的对应点,可知抛物线向右、向上各平移2个单位长度.
∵y=x2﹣x﹣=(x﹣1)2﹣2,∴平移后的抛物线为y=(x﹣3)2,其顶点坐标为(3,0);
∵原抛物线与新抛物线都经过点B(3,0),∴点B即为新抛物线与原抛物线的交点F.
作A′K⊥x轴于点K,则∠AKA′=∠FKA′=90°,AK=A′K=FK=2,
∴∠AA′K=∠FA′K=45°,∴∠AA′F=90°.由,得或(不符合题意,舍去),∴D(5,6),∴FD==2.
①当FP1=FD时,则点P1与点D关于点A′对称,∴P1(﹣3,﹣2);
②当P2D=FD=2时,∵CD=×5=5,∴CP2=5﹣2,
∴xp=×(5﹣2)=5,yp=5+1=6,P2(5,6);
③当DP3=FP3时,∵∠P3DF=∠FDP1,∠DFP3=∠DP1F,∴△P3DF∽△FDP1,
∴,∵DP1=×(5+3)=8,∴P3D===,
∴CP3=﹣=,∴xp=×=,yp==,∴P3(,);
④当P4D=FD=时,则CP4=+,
∴xp=×(+)=5+2,yp=5+2+1=6+2,
∴P4(5+,6+).
综上所述,点P的坐标为(﹣3,﹣2)或(5,6)或(,)或(5+,6+).
26.如图,已知在直角△ABC中,∠ABC=90°,E为AC边上一点,连接BE,过E作ED⊥AC,交BC边于点D.
(1)如图1,连接AD,若CE=2,BD=3,∠C=45°,求△ADE的面积;
(2)如图2,作∠ABC的角平分线交AC于点F,连接DF,若∠BDE=∠CDF,求证:AE+DE=BE;
(3)如图3,若∠C=30°,将△BCE沿BE折叠,得到△BEF,且BF与AC交于点G,连接AD,DF,点E在AC边上运动的过程中,当BF⊥AC时,直接写出的值.
【解答】(1)解:∵ED⊥AC,∠C=45°,∴∠EDC=∠C=45°,∴CE=DE=2,
∴,∵,∴,
在直角△ABC中,∠ABC=90°,∠C=45°,∴∠BAC=∠C=45°,∴,
∴,∴AE=AC﹣CE=8,;
(2)证明:如图2中,过点B作BT⊥BE交ED的延长线于点T.
∵∠BDE=∠CDF,∴∠CDE=∠BDF,∵DE⊥AC,
∴∠DEC=∠ABC=90°,∴∠A+∠C=∠EDC+∠C=90°,
∴∠EDC=∠A,∴∠A=∠BDF,∵∠ABF=∠DBF,BF=BF,
∴△ABF≌△DBF(SAS),∴AB=BD,∵∠ABC=∠EBT=90°,
∴∠ABE=∠DBT,∵∠BDT=∠CDE=∠A,∴△ABE≌△DBT(ASA),
∴BE=BT,AE=DT,∴AE+DE=DT+DE=ET,
∴△BET是等腰直角三角形,∴,∴;
(3)解:如图,
∵∠C=30°,∴∠BAC=60°,当BF⊥AC时,∠ABG=30°,
∵将△BCE沿BE折叠,得到△BEF,∴∠FBE=∠CBE=30°,
又∠C=∠EBC=30°,∴EB=EC,EB=EA,
∴△ABE是等边三角形,设AB=a,则AC=2a,
∴,∴BF=2BG=2×GE=AE=a,
∵BD=a,在Rt△ABD中,AD=2BD=a,如图,连接AF,
∵GE⊥BF,EF=EB,
∴∠AEF=∠AEB=60°,
∴△AFE是等边三角形,
∴AF=AE=AB,
∴∠FAD=∠FAE+∠EAD=60°+30°=90°,
∴DF===,
∴==.
同课章节目录
