2014-2015学年山东省泰安市高一(下)期末数学试卷(解析版)
文档属性
| 名称 | 2014-2015学年山东省泰安市高一(下)期末数学试卷(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 212.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-04 22:05:54 | ||
图片预览




文档简介
本资料来自于资源最齐全的21世纪教育网www.21cnjy.com
2014-2015学年山东省泰安市高一(下)期末数学试卷
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.2-1-c-n-j-y
1.(2015春 泰安期末)下列各角与角420°终边相同的是( )
A. 30° B. 60° C. 120° D. 300°
考点: 终边相同的角.
专题: 三角函数的求值.
分析: 利用终边相同的角的集合定理即可得出.
解答: 解:∵420°=360°+60°,
∴与角420°终边相同的是60°.
故选:B.
点评: 本题考查了终边相同的角的集合定理,属于基础题.
2.(2015春 泰安期末)从1,2,4,8这4个数中一次随机地取两个数,则所取两个数的乘积为8的概率是( )【来源:21cnj*y.co*m】
A. B. C. D.
考点: 列举法计算基本事件数及事件发生的概率.
专题: 概率与统计.
分析: 首先列举并求出“从1,2,4,8 ( http: / / www.21cnjy.com )这4个数中一次随机抽取2个数”的基本事件的个数再从中找到满足“所取2个数的乘积为8”的事件的个数,利用概率公式计算即可.
解答: 解:从1,2,4,8这4个数中一次 ( http: / / www.21cnjy.com )随机抽取2个数的所有基本事件有(1,2),(1,4),(1,8),(2,4),(2,8),(4,8)共6个,【版权所有:21教育】
所取2个数的乘积为8的基本事件有(1,8),(2,4)共2个,
故所求概率P==.
故选:C.
点评: 本题主要考查了古典概型的概率公式的应用,关键是一一列举出所有的基本事件.
3.(2012 湖南)设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x﹣85.71,则下列结论中不正确的是( )21教育名师原创作品
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(,)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重必为58.79kg
考点: 回归分析的初步应用.
专题: 阅读型.
分析: 根据回归方程为=0.85x﹣85.71,0.85>0,可知A,B,C均正确,对于D回归方程只能进行预测,但不可断定.
解答: 解:对于A,0.85>0,所以y与x具有正的线性相关关系,故正确;
对于B,回归直线过样本点的中心(,),故正确;
对于C,∵回归方程为=0.85x﹣85.71,∴该大学某女生身高增加1cm,则其体重约增加0.85kg,故正确;
对于D,x=170cm时,=0.85×170﹣85.71=58.79,但这是预测值,不可断定其体重为58.79kg,故不正确
故选D.
点评: 本题考查线性回归方程,考查学生对线性回归方程的理解,属于中档题.
4.(2015春 泰安期末)已知cosα=,α是第一象限角,则sin(π+α)的值为( )
A. B. ﹣ C. D. ﹣
考点: 同角三角函数基本关系的运用;运用诱导公式化简求值.
专题: 三角函数的求值.
分析: 由cosα的值及α的范围,利用同角三角函数间基本关系求出sinα的值,原式利用诱导公式化简将sinα的值代入计算即可求出值.
解答: 解:∵cosα=,α是第一象限角,
∴sinα==,
则sin(π+α)=﹣sinα=﹣,
故选:D.
点评: 此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键.
5.(2015春 泰安期末)已知向量=(1,k),=(9,k﹣6),若∥,则实数k的值为( )
A. ﹣ B. C. 3 D. 3+3
考点: 平面向量共线(平行)的坐标表示.
专题: 平面向量及应用.
分析: 利用向量平行得到坐标的等式解之.
解答: 解:因为向量=(1,k),=(9,k﹣6),∥,所以1×(k﹣6)=9k,8k+6=0,解得k=;
故选:A.
点评: 本题考查了平面向量的平行时的坐标关系;熟记向量平行的性质是关键.
6.(2015春 泰安期末)先将函数y=sin2x的图象向右平移个长度单位,然后将所得图象横坐标缩短到原来的,纵坐标不变,此时函数的解析式为( )
A. y=sin(4x﹣) B. y=sin(4x﹣) C. y=sin(x﹣) D. y=sin(x﹣) 21*cnjy*com
考点: 函数y=Asin(ωx+φ)的图象变换.
专题: 三角函数的图像与性质.
分析: 根据三角函数的平移变换,周期变换之间的关系即可得到结论.
解答: 解:将函数y=sin2x图象上所有点向右平移个单位,
所得图象的解析式为y=sin2(x﹣)=sin(2x﹣),
然后把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),
得到解析式为y=sin(4x﹣).
故选:A.
点评: 本题考查了y=Asin(ωx+φ)型函数图象的平移,注意变化顺序是关键,是中档题.
7.(2015春 泰安期末)已知菱形ABCD的边长为a,∠ABC=120°,则 =( )
A. ﹣a2 B. ﹣a2 C. a2 D. a2
考点: 平面向量数量积的运算.
专题: 平面向量及应用.
分析: 将所求利用菱形的相邻两边对应的向量表示,展开,利用菱形的性质转化为向量的计算.
解答: 解:菱形ABCD的边长为a,∠ABC=120°,则 =()==a2+a2cos120°=a2﹣a2=;
故选:C.
点评: 本题考查了菱形的性质运用以及平面向量的数量积、平行四边形法则的运用;关键是将所求转化为菱形相邻邻边为基底表示的向量.
8.(2013 重庆)以下茎叶图记录了甲、 ( http: / / www.21cnjy.com )乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )
( http: / / www.21cnjy.com )
A. 2,5 B. 5,5 C. 5,8 D. 8,8
考点: 茎叶图.
专题: 概率与统计.
分析: 求乙组数据的平均数 ( http: / / www.21cnjy.com )就是把所有乙组数据加起来,再除以5.找甲组数据的中位数要把甲组数据按从小到大的顺序排列,位于最中间的一个数为中位数.据此列式求解即可.
解答: 解:乙组数据平均数=(9+15+18+24+10+y)÷5=16.8;
∴y=8;
甲组数据可排列成:9,12,10+x,24,27.所以中位数为:10+x=15,
∴x=5.
故选:C.
点评: 本题考查了中位数和平均数的计算 ( http: / / www.21cnjy.com ).平均数是指在一组数据中所有数据之和再除以数据的个数.将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.
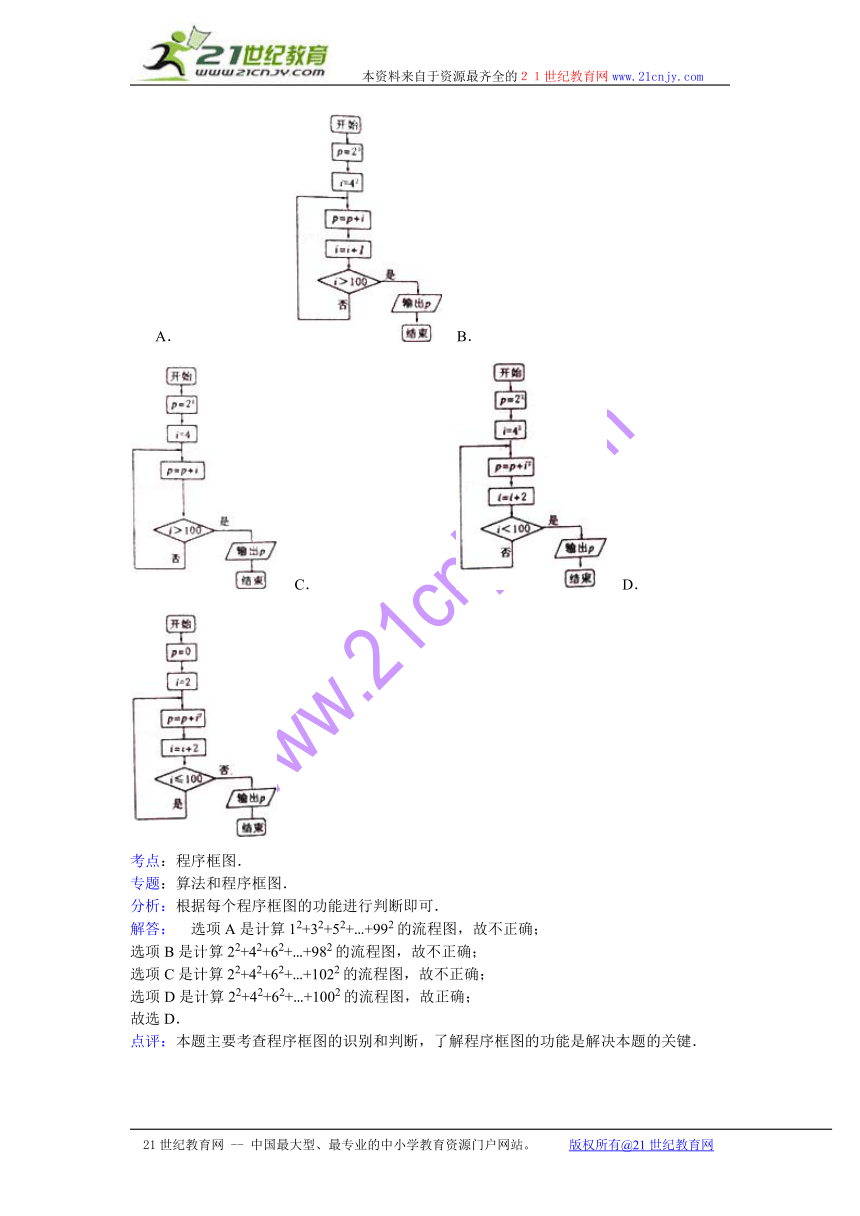
9.(2015春 泰安期末)计算22+42+62+…+1002的算法的程序框图是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
考点: 程序框图.
专题: 算法和程序框图.
分析: 根据每个程序框图的功能进行判断即可.
解答: 选项A是计算12+32+52+…+992的流程图,故不正确;
选项B是计算22+42+62+…+982的流程图,故不正确;
选项C是计算22+42+62+…+1022的流程图,故不正确;
选项D是计算22+42+62+…+1002的流程图,故正确;
故选D.
点评: 本题主要考查程序框图的识别和判断,了解程序框图的功能是解决本题的关键.
10.(2015春 泰安期末)已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点对称,且在区间上是单调函数,则ω的值为( )
A. B. C. D.
考点: y=Asin(ωx+φ)中参数的物理意义.
专题: 三角函数的图像与性质.
分析: 由f(x)是偶函数可得φ的值,利用图象关于点M对称,得f(﹣x)=﹣f(+x),可得ω的可能取值,结合单调函数可确定ω的值.
解答: 解:由f(x)是偶函数,得f(﹣x)=f(x),即sin(﹣ωx+ )=sin(ωx+ ),
所以﹣cosφsinωx=cosφsinωx,
对任意x都成立,且ω>0,所以得cosφ=0.
依题设0<φ<π,所以解得φ=,
由f(x)的图象关于点M对称,得f(﹣x)=﹣f(+x),
取x=0,得f()=sin(+)=cos,
∴f()=sin(+)=cos,∴cos=0,
又ω>0,得=+kπ,k=1,2,3,
∴ω=(2k+1),k=0,1,2,
当k=0时,ω=,f(x)=sin(x+)在[0,]上是减函数,满足题意;
当k=1时,ω=2,f(x)=sin(2x+)在[0,]上是减函数;
当k=2时,ω=,f(x)=(x+)在[0,]上不是单调函数;
所以,综合得ω=或2.
故选D.
点评: 本题主要考查三角函数的图象、单调性、奇偶性等基本知识,以及分析问题和推理计算能力,属于中档题.
二、填空题:本大题共5小题,每小题5分,共25分.
11.(2015春 泰安期末)若扇形的周长为6,面积为2,则扇形的圆心角的弧度数为 1或4 .
考点: 扇形面积公式.
专题: 计算题.
分析: 设扇形的圆心角的弧度数为α,圆的半径为r,利用扇形的周长为6,面积为2,即可求得扇形的圆心角的弧度数.【来源:21·世纪·教育·网】
解答: 解:设扇形的圆心角的弧度数为α,圆的半径为r,则
∴或
故答案为:1或4
点评: 本题考查扇形的周长与面积公式,解题的关键是建立方程组,属于基础题.
12.(2013 江西)设,为单位向量.且、的夹角为,若=+3,=2,则向量在方向上的射影为 .
考点: 平面向量数量积的运算.
专题: 平面向量及应用.
分析: 根据题意求得的值,从而求得的值,再根据在上的射影为 ,运算求得结果.
解答: 解:∵、为单位向量,且 和 的夹角θ等于,∴=1×1×cos=.
∵=+3,=2,∴=(+3) (2)=2+6=2+3=5.
∴在上的射影为 =,
故答案为 .
点评: 本题主要考查两个向量的数量积的运算,一个向量在另一个向量上的射影的定义,属于中档题.
13.(2013 福建)利用计算机产生0~1之间的均匀随机数a,则事件“3a﹣1>0”发生的概率为 .
考点: 几何概型.
专题: 概率与统计.
分析: 本题考查的知识点是几何概型 ( http: / / www.21cnjy.com )的意义,关键是要找出(0,1)上产生随机数a所对应图形的长度,及事件“3a﹣1>0”对应的图形的长度,并将其代入几何概型计算公式,进行求解.
解答: 解:3a﹣1>0即a>,
则事件“3a﹣1>0”发生的概率为P==.
故答案为:.
点评: 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.【出处:21教育名师】
14.(2015春 泰安期末)已知tanα=2,tanβ=,π<α<,0<β<π,则α﹣β的值为 .
考点: 两角和与差的正切函数.
专题: 三角函数的求值.
分析: 由题意可得α﹣β∈(0,),求得tan(α﹣β)==﹣1,可得α﹣β的值.
解答: 解:由题意可得α﹣β∈(0,),再根据tanα=2,tanβ=,求得tan(α﹣β)===﹣1,21*cnjy*com
∴α﹣β=,
故答案为:.
点评: 本题主要考查两角和差的正切公式,根据三角函数的值求角,属于基础题.
15.(2015春 泰安期末)连掷两次骰子分别得到点数m,n,向量=(m,n),=(﹣1,1),若△ABC中与同向,与反向,则∠ABC是钝角的概率是 .
考点: 几何概型.
专题: 平面向量及应用.
分析: 掷两次骰子分别得到的点数m ( http: / / www.21cnjy.com ),n,组成的向量(m,n)个数为36个,与向量(﹣1,1)的夹角θ>90°的这个事件包含的基本事件数须将其满足的条件进行转化,再进行研究
解答: 解:连掷两次骰子分别得到点数m,n,所组成的向量(m,n)的个数共有36种.
由于向量(m,n)与向量(﹣1,1)的夹角θ>90°时,
∴(m,n) (﹣1,1)<0,并且m+n≠0,满足题意的情况如下
当m=2时,n=1; 当m=3时,n=1,2;
当m=4时,n=1,2,3; 当m=5时,n=1,2,3,4;
当m=6时,n=1,2,3,4,5; 共有15种.
∠ABC是钝角,即向量(m,n)与向量(﹣1,1)的夹角θ>90°.
故所求事件的概率是 ;
故答案为:
点评: 本题考查古典概型概率求法,考查了概率与向量相结合,以及分类计数的技巧,有一定的综合性.
三、解答题:本大题共6个小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤.
16.(2015春 泰安期末)设计一个算法,求实数x的绝对值,并画出程序框图.
考点: 设计程序框图解决实际问题.
专题: 应用题;算法和程序框图.
分析: 利用条件语句可写出相应的算法,利用选择结构画出程序框图.
解答: (本题满分12分)
解:第一步,输入一个实数x,
第二步,判断x的符号,若x≥0,则输出x,否则,输出﹣x…6分
程序框图如下:
( http: / / www.21cnjy.com )…12分
点评: 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视,本题属于基础题.
17.(2015春 泰安期末) 已知函数f(x)=sin(2x﹣)
(1)用“五点法”在所给的直角坐标系中画出f(x)在[0,π]内的简图.
(2)求函数f(x)的周期和单调递增区间.
( http: / / www.21cnjy.com )
考点: 五点法作函数y=Asin(ωx+φ)的图象;正弦函数的图象.
分析: (1)利用列表法,结合五点作图法进行取值作图.
(2)根据三角函数的单调性的性质进行求解即可.
解答: 解:(1)
2x﹣ π
x 0 π
y 0 1 0 ﹣1
对应的图象为
(2)三角函数的周期T=,
由2kπ﹣≤2x﹣≤2kπ+,k∈Z,
解得kπ≤x≤2kπ+,k∈Z,
即函数f(x)的单调递增区间为[kπ,2kπ+],k∈Z.
( http: / / www.21cnjy.com )
点评: 本题主要考查三角函数的图象和性质,要求熟练掌握相应的三角函数的性质以及五点法作图.
18.(2015春 泰安期末)某中学调查了某班全部50名同学参加数学兴趣小组和物理兴趣小组的情况,数据如下表:(单位:人)21cnjy.com
参加数学兴趣小组 不参加数学兴趣小组
参加物理兴趣小组 7 10
不参加物理兴趣小组 7 26
(Ⅰ)从该班随机选一名同学,求该同学至少参加上述一个兴趣小组的概率;
(Ⅱ)在既参加数学兴趣小组,又参加物理兴趣小 ( http: / / www.21cnjy.com )组的7名同学中,有4名男同学A,B,C,D,3名女同学a,b,c,现从这4名男同学和3名女同学中各随机选1人,求A被选中且a未被选中的概率.www.21-cn-jy.com
考点: 列举法计算基本事件数及事件发生的概率.
专题: 概率与统计.
分析: (Ⅰ)先判断出这是 ( http: / / www.21cnjy.com )一个古典概型,所以求出基本事件总数,“至少参加上述一个兴趣小组”事件包含的基本事件个数,从而根据古典概型的概率计算公式计算即可;
(Ⅱ)列举所有的基本事件,然后根据古典概型的概率公式计算即可.
解答: 解:(Ⅰ)设“至少参加上述一个兴趣小组”为事件A;
从50名同学中任选一名有50种选法,
∴基本事件数为50﹣26=24;
∴P(A)==;
(Ⅱ)现从这4名男同学和 ( http: / / www.21cnjy.com )3名女同学中各随机选1人,其一切可能的结果组成的基本事件有:Aa,Ab,Ac,Ba,Bb,Bc,Ca,Cb,Cc.Da,Db,Dc,共12个,
“A被选中且a未被选中”所包含的基本事件有Ab,Ac,共2个,
故A被选中且a未被选中的概率P==.
点评: 考查古典概型的概念,以及古典概型的概率的求法,属于基础题.
19.(2015春 泰安期末)某所高中 ( http: / / www.21cnjy.com )为了调查本校高一年级学生一周内课外阅读的投入时间(单位:小时)的情况,学校教务处对该校高一1500名在校生进行了随机编号,从0001号到1500号,抽取编号最后一位数字为3的150名学生进行问卷调查,搜集得到了这150名学生一周课外阅读时间的数据,将数据分成8个组,分组区间为:[1,3),[3,5),[5,7),…,[13,15),[15,17],其频率分布直方图如图:
(Ⅰ)该校问卷调查环节抽取样本过程中,运用了哪种抽样方法;
(Ⅱ)求频率分布直方图中a的值;并求落在区间[9,11)中的学生人数b;
(Ⅲ)根据频率分布直方图,估计本校高一年级学生周课外阅读时间的平均数.
( http: / / www.21cnjy.com )
考点: 众数、中位数、平均数;频率分布直方图.
专题: 应用题;概率与统计.
分析: (Ⅰ)根据抽样方法的特征,得出抽样方法是系统抽样;
(Ⅱ)根据频率和为1,求出a的值,再计算落在区间[9,11)中的频率与频数;
(Ⅲ)根据频率分布直方图,计算样本平均数,由此估计总体平均数.
解答: 解:(Ⅰ)先对学生随机编号,从所编的号码中抽取编号最后一位数字为3的150名学生进行问卷调查,
符合系统抽样的方法特征,应是系统抽样;
(Ⅱ)由频率分布直方图知,
(2a+4a×2+5a+7a+8a+9a+11a)×2=1,
即100a=1,
解得a=0.01;
落在区间[9,11)中的频率为
11a×2=0.22,
落在该区间内的学生人数为
b=0.22×150=33;
(Ⅲ)根据频率分布直方图,估计样本中150名学生周课外阅读时间的平均数为
2×0.08+4×0.1+6×0.14+8×0.18+10×0.22+12×0.16+14×0.08+16×0.04
=0.16+0.4+0.84+1.44+2.2+1.92+1.12+0.64
=8.72,
由此估计本校高一年级学生周课外阅读时间的平均数为8.72小时.
点评: 本题考查了抽样方法的应用问题,也考查了频率分布直方图的应用问题,考查了平均数的计算问题,是基础题目.21教育网
20.(2015春 泰安期末)已知向量=(4sinx,1),=(cos(x+),1)
(Ⅰ)设函数f(x)= ,求函数f(x)在区间[0,]上的最大值和最小值;
(Ⅱ)若f()=,<A<π,求cos2A的值.
考点: 三角函数中的恒等变换应用;平面向量数量积的运算.
专题: 三角函数的求值;三角函数的图像与性质;平面向量及应用.
分析: (Ⅰ)由平面向量数量积的运算及三角函数中的恒等变换应用可得f(x)=2in(2x+),根据正弦函数的单调性即可求得函数f(x)在区间[0,]上的最大值和最小值;
(Ⅱ)由已知可得sin(A+)=,结合A的范围,可求cos(A+)=﹣,从而可求cosA=cos(A+﹣)的值,利用二倍角的余弦函数公式即可得解.
解答: 解:(Ⅰ)∵f(x)= =4sinxcos(x+)+1
=4sinx(cosx﹣sinx)+1
=(2sinxcosx)+(1﹣2sin2x)
=sin2x+cos2x
=2in(2x+),
∵f(x)=2in(2x+)在区间[0,]上为增函数,在区间[,]上为减函数,
又∵f(0)=1,f()=2,f()=﹣1,
∴函数f(x)在区间[0,]上的最大值为2,最小值为﹣1.…7分
(Ⅱ)∵f()=,
∴sin(A+)=,
又∵,
∴<A+<π,
∴cos(A+)=﹣,
∴cosA=cos(A+﹣)=cos(A+)cos+sin(A+)sin=,
∴cos2A=2cos2A﹣1
=2﹣1
=.…13分
点评: 本题主要考查了平面向量数量积的运算,三角函数中的恒等变换应用,正弦函数的单调性,二倍角的余弦函数公式的应用,属于基本知识的考查.21世纪教育网版权所有
21.(2015春 泰安期末)如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),=+.
(Ⅰ)若=x+y,其中x,y∈R,求x+y的最大值;
(Ⅱ)当 +sinθ≥+1时,求θ的取值范围.
( http: / / www.21cnjy.com )
考点: 平面向量数量积的运算;向量的线性运算性质及几何意义.
专题: 平面向量及应用.
分析: (Ⅰ)由已知,根据三角函数的定义得到A,B,P的坐标,将=x+y表示为以θ为参数的方程,x+y用θ的三角函数表示求最值;21·cn·jy·com
(Ⅱ)由(Ⅰ)得到 +sinθ用坐标表示后化简得到关于θ的三角函数值的范围,进而求θ的取值范围.2·1·c·n·j·y
解答: 解:(Ⅰ)由任意角的三角函数的定义得到A(1,0),B(),P(cosθ,sinθ),
因为=x+y,所以 ( http: / / www.21cnjy.com ),解得 ( http: / / www.21cnjy.com ),所以x+y=sinθ+cosθ=2sin(),
因为0<θ<π,所以当θ=时,x+y的最大值为2;
(Ⅱ)因为=+=(1+cosθ,sinθ),
所以 +sinθ=1+cosθ+sinθ=sin()+1≥+1,
整理得sin(),所以2kπ+≤≤2kπ+,k∈Z,所以2kπ+≤θ≤2kπ+,k∈Z,21·世纪*教育网
由于0<θ<π,所以,即.
点评: 本题考查了三角函数的坐标法定义的运用、平面向量的坐标运算以及三角函数的最值求法;关键是将问题坐标化.www-2-1-cnjy-com
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
2014-2015学年山东省泰安市高一(下)期末数学试卷
一、选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.2-1-c-n-j-y
1.(2015春 泰安期末)下列各角与角420°终边相同的是( )
A. 30° B. 60° C. 120° D. 300°
考点: 终边相同的角.
专题: 三角函数的求值.
分析: 利用终边相同的角的集合定理即可得出.
解答: 解:∵420°=360°+60°,
∴与角420°终边相同的是60°.
故选:B.
点评: 本题考查了终边相同的角的集合定理,属于基础题.
2.(2015春 泰安期末)从1,2,4,8这4个数中一次随机地取两个数,则所取两个数的乘积为8的概率是( )【来源:21cnj*y.co*m】
A. B. C. D.
考点: 列举法计算基本事件数及事件发生的概率.
专题: 概率与统计.
分析: 首先列举并求出“从1,2,4,8 ( http: / / www.21cnjy.com )这4个数中一次随机抽取2个数”的基本事件的个数再从中找到满足“所取2个数的乘积为8”的事件的个数,利用概率公式计算即可.
解答: 解:从1,2,4,8这4个数中一次 ( http: / / www.21cnjy.com )随机抽取2个数的所有基本事件有(1,2),(1,4),(1,8),(2,4),(2,8),(4,8)共6个,【版权所有:21教育】
所取2个数的乘积为8的基本事件有(1,8),(2,4)共2个,
故所求概率P==.
故选:C.
点评: 本题主要考查了古典概型的概率公式的应用,关键是一一列举出所有的基本事件.
3.(2012 湖南)设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x﹣85.71,则下列结论中不正确的是( )21教育名师原创作品
A. y与x具有正的线性相关关系
B. 回归直线过样本点的中心(,)
C. 若该大学某女生身高增加1cm,则其体重约增加0.85kg
D. 若该大学某女生身高为170cm,则可断定其体重必为58.79kg
考点: 回归分析的初步应用.
专题: 阅读型.
分析: 根据回归方程为=0.85x﹣85.71,0.85>0,可知A,B,C均正确,对于D回归方程只能进行预测,但不可断定.
解答: 解:对于A,0.85>0,所以y与x具有正的线性相关关系,故正确;
对于B,回归直线过样本点的中心(,),故正确;
对于C,∵回归方程为=0.85x﹣85.71,∴该大学某女生身高增加1cm,则其体重约增加0.85kg,故正确;
对于D,x=170cm时,=0.85×170﹣85.71=58.79,但这是预测值,不可断定其体重为58.79kg,故不正确
故选D.
点评: 本题考查线性回归方程,考查学生对线性回归方程的理解,属于中档题.
4.(2015春 泰安期末)已知cosα=,α是第一象限角,则sin(π+α)的值为( )
A. B. ﹣ C. D. ﹣
考点: 同角三角函数基本关系的运用;运用诱导公式化简求值.
专题: 三角函数的求值.
分析: 由cosα的值及α的范围,利用同角三角函数间基本关系求出sinα的值,原式利用诱导公式化简将sinα的值代入计算即可求出值.
解答: 解:∵cosα=,α是第一象限角,
∴sinα==,
则sin(π+α)=﹣sinα=﹣,
故选:D.
点评: 此题考查了同角三角函数基本关系的运用,以及运用诱导公式化简求值,熟练掌握基本关系是解本题的关键.
5.(2015春 泰安期末)已知向量=(1,k),=(9,k﹣6),若∥,则实数k的值为( )
A. ﹣ B. C. 3 D. 3+3
考点: 平面向量共线(平行)的坐标表示.
专题: 平面向量及应用.
分析: 利用向量平行得到坐标的等式解之.
解答: 解:因为向量=(1,k),=(9,k﹣6),∥,所以1×(k﹣6)=9k,8k+6=0,解得k=;
故选:A.
点评: 本题考查了平面向量的平行时的坐标关系;熟记向量平行的性质是关键.
6.(2015春 泰安期末)先将函数y=sin2x的图象向右平移个长度单位,然后将所得图象横坐标缩短到原来的,纵坐标不变,此时函数的解析式为( )
A. y=sin(4x﹣) B. y=sin(4x﹣) C. y=sin(x﹣) D. y=sin(x﹣) 21*cnjy*com
考点: 函数y=Asin(ωx+φ)的图象变换.
专题: 三角函数的图像与性质.
分析: 根据三角函数的平移变换,周期变换之间的关系即可得到结论.
解答: 解:将函数y=sin2x图象上所有点向右平移个单位,
所得图象的解析式为y=sin2(x﹣)=sin(2x﹣),
然后把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),
得到解析式为y=sin(4x﹣).
故选:A.
点评: 本题考查了y=Asin(ωx+φ)型函数图象的平移,注意变化顺序是关键,是中档题.
7.(2015春 泰安期末)已知菱形ABCD的边长为a,∠ABC=120°,则 =( )
A. ﹣a2 B. ﹣a2 C. a2 D. a2
考点: 平面向量数量积的运算.
专题: 平面向量及应用.
分析: 将所求利用菱形的相邻两边对应的向量表示,展开,利用菱形的性质转化为向量的计算.
解答: 解:菱形ABCD的边长为a,∠ABC=120°,则 =()==a2+a2cos120°=a2﹣a2=;
故选:C.
点评: 本题考查了菱形的性质运用以及平面向量的数量积、平行四边形法则的运用;关键是将所求转化为菱形相邻邻边为基底表示的向量.
8.(2013 重庆)以下茎叶图记录了甲、 ( http: / / www.21cnjy.com )乙两组各五名学生在一次英语听力测试中的成绩(单位:分).已知甲组数据的中位数为15,乙组数据的平均数为16.8,则x,y的值分别为( )
( http: / / www.21cnjy.com )
A. 2,5 B. 5,5 C. 5,8 D. 8,8
考点: 茎叶图.
专题: 概率与统计.
分析: 求乙组数据的平均数 ( http: / / www.21cnjy.com )就是把所有乙组数据加起来,再除以5.找甲组数据的中位数要把甲组数据按从小到大的顺序排列,位于最中间的一个数为中位数.据此列式求解即可.
解答: 解:乙组数据平均数=(9+15+18+24+10+y)÷5=16.8;
∴y=8;
甲组数据可排列成:9,12,10+x,24,27.所以中位数为:10+x=15,
∴x=5.
故选:C.
点评: 本题考查了中位数和平均数的计算 ( http: / / www.21cnjy.com ).平均数是指在一组数据中所有数据之和再除以数据的个数.将一组数据从小到大依次排列,把中间数据(或中间两数据的平均数)叫做中位数.
9.(2015春 泰安期末)计算22+42+62+…+1002的算法的程序框图是( )
A. ( http: / / www.21cnjy.com ) B. ( http: / / www.21cnjy.com ) C. ( http: / / www.21cnjy.com ) D. ( http: / / www.21cnjy.com )
考点: 程序框图.
专题: 算法和程序框图.
分析: 根据每个程序框图的功能进行判断即可.
解答: 选项A是计算12+32+52+…+992的流程图,故不正确;
选项B是计算22+42+62+…+982的流程图,故不正确;
选项C是计算22+42+62+…+1022的流程图,故不正确;
选项D是计算22+42+62+…+1002的流程图,故正确;
故选D.
点评: 本题主要考查程序框图的识别和判断,了解程序框图的功能是解决本题的关键.
10.(2015春 泰安期末)已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)是R上的偶函数,其图象关于点对称,且在区间上是单调函数,则ω的值为( )
A. B. C. D.
考点: y=Asin(ωx+φ)中参数的物理意义.
专题: 三角函数的图像与性质.
分析: 由f(x)是偶函数可得φ的值,利用图象关于点M对称,得f(﹣x)=﹣f(+x),可得ω的可能取值,结合单调函数可确定ω的值.
解答: 解:由f(x)是偶函数,得f(﹣x)=f(x),即sin(﹣ωx+ )=sin(ωx+ ),
所以﹣cosφsinωx=cosφsinωx,
对任意x都成立,且ω>0,所以得cosφ=0.
依题设0<φ<π,所以解得φ=,
由f(x)的图象关于点M对称,得f(﹣x)=﹣f(+x),
取x=0,得f()=sin(+)=cos,
∴f()=sin(+)=cos,∴cos=0,
又ω>0,得=+kπ,k=1,2,3,
∴ω=(2k+1),k=0,1,2,
当k=0时,ω=,f(x)=sin(x+)在[0,]上是减函数,满足题意;
当k=1时,ω=2,f(x)=sin(2x+)在[0,]上是减函数;
当k=2时,ω=,f(x)=(x+)在[0,]上不是单调函数;
所以,综合得ω=或2.
故选D.
点评: 本题主要考查三角函数的图象、单调性、奇偶性等基本知识,以及分析问题和推理计算能力,属于中档题.
二、填空题:本大题共5小题,每小题5分,共25分.
11.(2015春 泰安期末)若扇形的周长为6,面积为2,则扇形的圆心角的弧度数为 1或4 .
考点: 扇形面积公式.
专题: 计算题.
分析: 设扇形的圆心角的弧度数为α,圆的半径为r,利用扇形的周长为6,面积为2,即可求得扇形的圆心角的弧度数.【来源:21·世纪·教育·网】
解答: 解:设扇形的圆心角的弧度数为α,圆的半径为r,则
∴或
故答案为:1或4
点评: 本题考查扇形的周长与面积公式,解题的关键是建立方程组,属于基础题.
12.(2013 江西)设,为单位向量.且、的夹角为,若=+3,=2,则向量在方向上的射影为 .
考点: 平面向量数量积的运算.
专题: 平面向量及应用.
分析: 根据题意求得的值,从而求得的值,再根据在上的射影为 ,运算求得结果.
解答: 解:∵、为单位向量,且 和 的夹角θ等于,∴=1×1×cos=.
∵=+3,=2,∴=(+3) (2)=2+6=2+3=5.
∴在上的射影为 =,
故答案为 .
点评: 本题主要考查两个向量的数量积的运算,一个向量在另一个向量上的射影的定义,属于中档题.
13.(2013 福建)利用计算机产生0~1之间的均匀随机数a,则事件“3a﹣1>0”发生的概率为 .
考点: 几何概型.
专题: 概率与统计.
分析: 本题考查的知识点是几何概型 ( http: / / www.21cnjy.com )的意义,关键是要找出(0,1)上产生随机数a所对应图形的长度,及事件“3a﹣1>0”对应的图形的长度,并将其代入几何概型计算公式,进行求解.
解答: 解:3a﹣1>0即a>,
则事件“3a﹣1>0”发生的概率为P==.
故答案为:.
点评: 几何概型的概率估算公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.【出处:21教育名师】
14.(2015春 泰安期末)已知tanα=2,tanβ=,π<α<,0<β<π,则α﹣β的值为 .
考点: 两角和与差的正切函数.
专题: 三角函数的求值.
分析: 由题意可得α﹣β∈(0,),求得tan(α﹣β)==﹣1,可得α﹣β的值.
解答: 解:由题意可得α﹣β∈(0,),再根据tanα=2,tanβ=,求得tan(α﹣β)===﹣1,21*cnjy*com
∴α﹣β=,
故答案为:.
点评: 本题主要考查两角和差的正切公式,根据三角函数的值求角,属于基础题.
15.(2015春 泰安期末)连掷两次骰子分别得到点数m,n,向量=(m,n),=(﹣1,1),若△ABC中与同向,与反向,则∠ABC是钝角的概率是 .
考点: 几何概型.
专题: 平面向量及应用.
分析: 掷两次骰子分别得到的点数m ( http: / / www.21cnjy.com ),n,组成的向量(m,n)个数为36个,与向量(﹣1,1)的夹角θ>90°的这个事件包含的基本事件数须将其满足的条件进行转化,再进行研究
解答: 解:连掷两次骰子分别得到点数m,n,所组成的向量(m,n)的个数共有36种.
由于向量(m,n)与向量(﹣1,1)的夹角θ>90°时,
∴(m,n) (﹣1,1)<0,并且m+n≠0,满足题意的情况如下
当m=2时,n=1; 当m=3时,n=1,2;
当m=4时,n=1,2,3; 当m=5时,n=1,2,3,4;
当m=6时,n=1,2,3,4,5; 共有15种.
∠ABC是钝角,即向量(m,n)与向量(﹣1,1)的夹角θ>90°.
故所求事件的概率是 ;
故答案为:
点评: 本题考查古典概型概率求法,考查了概率与向量相结合,以及分类计数的技巧,有一定的综合性.
三、解答题:本大题共6个小题,共75分,解答应写出必要的文字说明、证明过程或演算步骤.
16.(2015春 泰安期末)设计一个算法,求实数x的绝对值,并画出程序框图.
考点: 设计程序框图解决实际问题.
专题: 应用题;算法和程序框图.
分析: 利用条件语句可写出相应的算法,利用选择结构画出程序框图.
解答: (本题满分12分)
解:第一步,输入一个实数x,
第二步,判断x的符号,若x≥0,则输出x,否则,输出﹣x…6分
程序框图如下:
( http: / / www.21cnjy.com )…12分
点评: 算法是新课程中的新增加的内容,也必然是新高考中的一个热点,应高度重视,本题属于基础题.
17.(2015春 泰安期末) 已知函数f(x)=sin(2x﹣)
(1)用“五点法”在所给的直角坐标系中画出f(x)在[0,π]内的简图.
(2)求函数f(x)的周期和单调递增区间.
( http: / / www.21cnjy.com )
考点: 五点法作函数y=Asin(ωx+φ)的图象;正弦函数的图象.
分析: (1)利用列表法,结合五点作图法进行取值作图.
(2)根据三角函数的单调性的性质进行求解即可.
解答: 解:(1)
2x﹣ π
x 0 π
y 0 1 0 ﹣1
对应的图象为
(2)三角函数的周期T=,
由2kπ﹣≤2x﹣≤2kπ+,k∈Z,
解得kπ≤x≤2kπ+,k∈Z,
即函数f(x)的单调递增区间为[kπ,2kπ+],k∈Z.
( http: / / www.21cnjy.com )
点评: 本题主要考查三角函数的图象和性质,要求熟练掌握相应的三角函数的性质以及五点法作图.
18.(2015春 泰安期末)某中学调查了某班全部50名同学参加数学兴趣小组和物理兴趣小组的情况,数据如下表:(单位:人)21cnjy.com
参加数学兴趣小组 不参加数学兴趣小组
参加物理兴趣小组 7 10
不参加物理兴趣小组 7 26
(Ⅰ)从该班随机选一名同学,求该同学至少参加上述一个兴趣小组的概率;
(Ⅱ)在既参加数学兴趣小组,又参加物理兴趣小 ( http: / / www.21cnjy.com )组的7名同学中,有4名男同学A,B,C,D,3名女同学a,b,c,现从这4名男同学和3名女同学中各随机选1人,求A被选中且a未被选中的概率.www.21-cn-jy.com
考点: 列举法计算基本事件数及事件发生的概率.
专题: 概率与统计.
分析: (Ⅰ)先判断出这是 ( http: / / www.21cnjy.com )一个古典概型,所以求出基本事件总数,“至少参加上述一个兴趣小组”事件包含的基本事件个数,从而根据古典概型的概率计算公式计算即可;
(Ⅱ)列举所有的基本事件,然后根据古典概型的概率公式计算即可.
解答: 解:(Ⅰ)设“至少参加上述一个兴趣小组”为事件A;
从50名同学中任选一名有50种选法,
∴基本事件数为50﹣26=24;
∴P(A)==;
(Ⅱ)现从这4名男同学和 ( http: / / www.21cnjy.com )3名女同学中各随机选1人,其一切可能的结果组成的基本事件有:Aa,Ab,Ac,Ba,Bb,Bc,Ca,Cb,Cc.Da,Db,Dc,共12个,
“A被选中且a未被选中”所包含的基本事件有Ab,Ac,共2个,
故A被选中且a未被选中的概率P==.
点评: 考查古典概型的概念,以及古典概型的概率的求法,属于基础题.
19.(2015春 泰安期末)某所高中 ( http: / / www.21cnjy.com )为了调查本校高一年级学生一周内课外阅读的投入时间(单位:小时)的情况,学校教务处对该校高一1500名在校生进行了随机编号,从0001号到1500号,抽取编号最后一位数字为3的150名学生进行问卷调查,搜集得到了这150名学生一周课外阅读时间的数据,将数据分成8个组,分组区间为:[1,3),[3,5),[5,7),…,[13,15),[15,17],其频率分布直方图如图:
(Ⅰ)该校问卷调查环节抽取样本过程中,运用了哪种抽样方法;
(Ⅱ)求频率分布直方图中a的值;并求落在区间[9,11)中的学生人数b;
(Ⅲ)根据频率分布直方图,估计本校高一年级学生周课外阅读时间的平均数.
( http: / / www.21cnjy.com )
考点: 众数、中位数、平均数;频率分布直方图.
专题: 应用题;概率与统计.
分析: (Ⅰ)根据抽样方法的特征,得出抽样方法是系统抽样;
(Ⅱ)根据频率和为1,求出a的值,再计算落在区间[9,11)中的频率与频数;
(Ⅲ)根据频率分布直方图,计算样本平均数,由此估计总体平均数.
解答: 解:(Ⅰ)先对学生随机编号,从所编的号码中抽取编号最后一位数字为3的150名学生进行问卷调查,
符合系统抽样的方法特征,应是系统抽样;
(Ⅱ)由频率分布直方图知,
(2a+4a×2+5a+7a+8a+9a+11a)×2=1,
即100a=1,
解得a=0.01;
落在区间[9,11)中的频率为
11a×2=0.22,
落在该区间内的学生人数为
b=0.22×150=33;
(Ⅲ)根据频率分布直方图,估计样本中150名学生周课外阅读时间的平均数为
2×0.08+4×0.1+6×0.14+8×0.18+10×0.22+12×0.16+14×0.08+16×0.04
=0.16+0.4+0.84+1.44+2.2+1.92+1.12+0.64
=8.72,
由此估计本校高一年级学生周课外阅读时间的平均数为8.72小时.
点评: 本题考查了抽样方法的应用问题,也考查了频率分布直方图的应用问题,考查了平均数的计算问题,是基础题目.21教育网
20.(2015春 泰安期末)已知向量=(4sinx,1),=(cos(x+),1)
(Ⅰ)设函数f(x)= ,求函数f(x)在区间[0,]上的最大值和最小值;
(Ⅱ)若f()=,<A<π,求cos2A的值.
考点: 三角函数中的恒等变换应用;平面向量数量积的运算.
专题: 三角函数的求值;三角函数的图像与性质;平面向量及应用.
分析: (Ⅰ)由平面向量数量积的运算及三角函数中的恒等变换应用可得f(x)=2in(2x+),根据正弦函数的单调性即可求得函数f(x)在区间[0,]上的最大值和最小值;
(Ⅱ)由已知可得sin(A+)=,结合A的范围,可求cos(A+)=﹣,从而可求cosA=cos(A+﹣)的值,利用二倍角的余弦函数公式即可得解.
解答: 解:(Ⅰ)∵f(x)= =4sinxcos(x+)+1
=4sinx(cosx﹣sinx)+1
=(2sinxcosx)+(1﹣2sin2x)
=sin2x+cos2x
=2in(2x+),
∵f(x)=2in(2x+)在区间[0,]上为增函数,在区间[,]上为减函数,
又∵f(0)=1,f()=2,f()=﹣1,
∴函数f(x)在区间[0,]上的最大值为2,最小值为﹣1.…7分
(Ⅱ)∵f()=,
∴sin(A+)=,
又∵,
∴<A+<π,
∴cos(A+)=﹣,
∴cosA=cos(A+﹣)=cos(A+)cos+sin(A+)sin=,
∴cos2A=2cos2A﹣1
=2﹣1
=.…13分
点评: 本题主要考查了平面向量数量积的运算,三角函数中的恒等变换应用,正弦函数的单调性,二倍角的余弦函数公式的应用,属于基本知识的考查.21世纪教育网版权所有
21.(2015春 泰安期末)如图,点A是单位圆与x轴正半轴的交点,点B是单位圆上一个定点,点P是一个动点,且∠AOB=120°,∠AOP=θ(0<θ<π),=+.
(Ⅰ)若=x+y,其中x,y∈R,求x+y的最大值;
(Ⅱ)当 +sinθ≥+1时,求θ的取值范围.
( http: / / www.21cnjy.com )
考点: 平面向量数量积的运算;向量的线性运算性质及几何意义.
专题: 平面向量及应用.
分析: (Ⅰ)由已知,根据三角函数的定义得到A,B,P的坐标,将=x+y表示为以θ为参数的方程,x+y用θ的三角函数表示求最值;21·cn·jy·com
(Ⅱ)由(Ⅰ)得到 +sinθ用坐标表示后化简得到关于θ的三角函数值的范围,进而求θ的取值范围.2·1·c·n·j·y
解答: 解:(Ⅰ)由任意角的三角函数的定义得到A(1,0),B(),P(cosθ,sinθ),
因为=x+y,所以 ( http: / / www.21cnjy.com ),解得 ( http: / / www.21cnjy.com ),所以x+y=sinθ+cosθ=2sin(),
因为0<θ<π,所以当θ=时,x+y的最大值为2;
(Ⅱ)因为=+=(1+cosθ,sinθ),
所以 +sinθ=1+cosθ+sinθ=sin()+1≥+1,
整理得sin(),所以2kπ+≤≤2kπ+,k∈Z,所以2kπ+≤θ≤2kπ+,k∈Z,21·世纪*教育网
由于0<θ<π,所以,即.
点评: 本题考查了三角函数的坐标法定义的运用、平面向量的坐标运算以及三角函数的最值求法;关键是将问题坐标化.www-2-1-cnjy-com
21世纪教育网 -- 中国最大型、最专业的中小学教育资源门户网站。 版权所有@21世纪教育网
同课章节目录
