18.1勾股定理
图片预览






文档简介
课件24张PPT。第十八章 勾股定理
18.1 勾股定理行唐二中 刘华 勾股定理证
明应
用小
结猜
想练
习史
话观察思考 相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。同学们,我们也来观察下图中的地面,看看能发现些什么?
得出结论:
以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
即
在等腰直角三角形中,两直角边的平方和等于斜边的平方.一起探究 等腰直角三角形三边之间有上述性质,那么其他的直角三角形三边是否也具有上述性质呢?
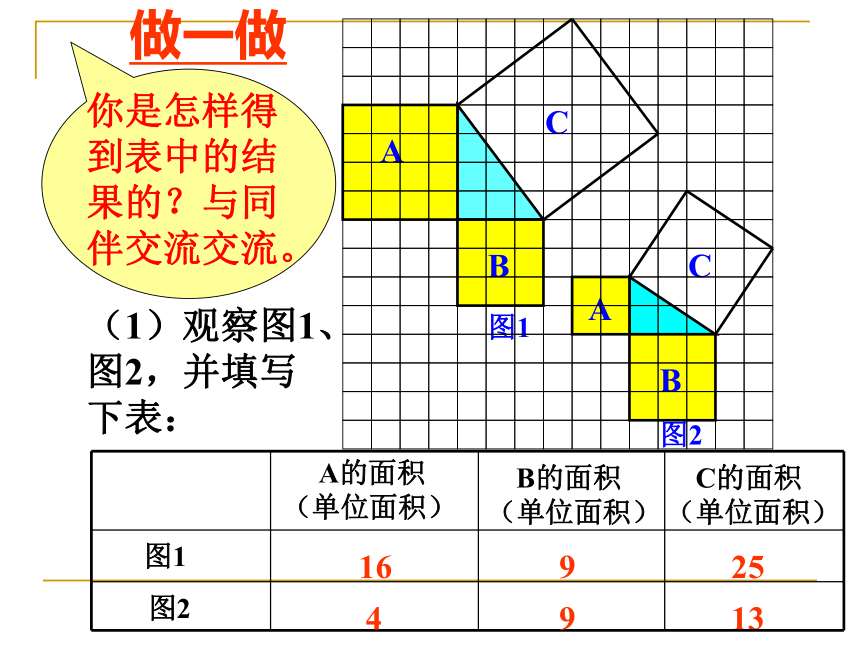
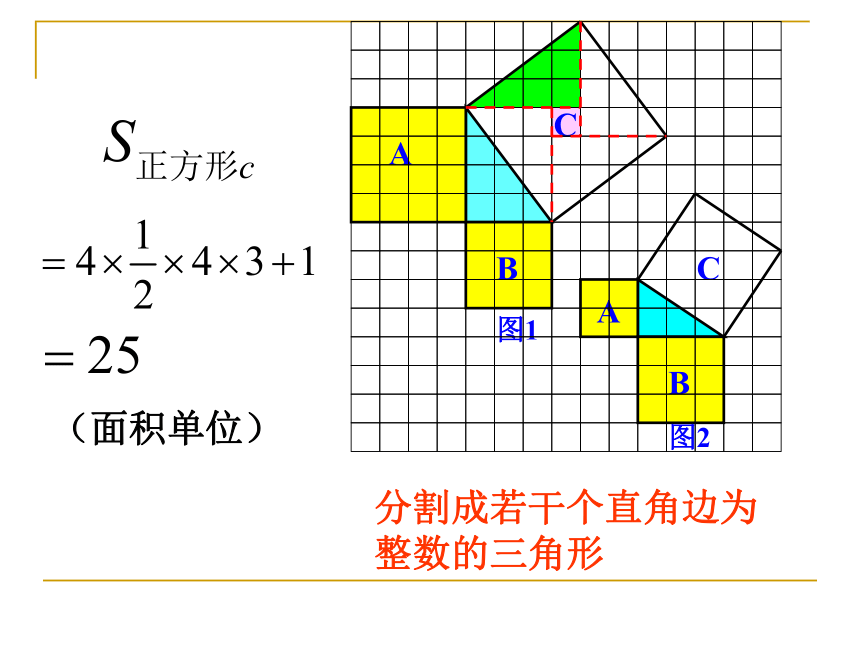
请用网格纸动手画一画,量一量,和同桌交流想法. C的面积(单位面积)1325(1)观察图1、图2,并填写下表: A的面积(单位面积) B的面积(单位面积) 图1 图216949做一做分割成若干个直角边为整数的三角形(面积单位)(2)三个正方形A,B,C的面积之间有什么关系?SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积 命题1 如果直角三角形的两直角边长分别为a、b,斜边长为c,那么: 猜想:左图的面积为 右图的面积为
a2+b2 c2
可知 a2+b2=C2
试一试 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.所以命题1叫勾股定理. 经过证明被确认正确的命题叫定理. 如果直角三角形的两直角边长分别为a、b,斜边长为c,那么: 勾a股b弦 c勾股定理(gou-gu theorem) 在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”即:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。故称之为“勾股定理”或“商高定理”史话勾股定理 在西方,希腊数学家欧几里德(Euclid,公元前三百年左右)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了。 毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。 相传,毕达哥拉斯学派找到了勾股定理的证明后,欣喜若狂,杀了一百头牛祭神,由此,又有“百牛定理”之称。拓广应用1. 一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?分析:
连结AC,在Rt△ABC中,根据勾股定理:
因此,
因为AC大于木板的宽,所以木板能从门框内通过。拓广应用2.
一个3m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.5m.如果梯子顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
分析:在Rt△ABC中,
在Rt△DCE中,
所以梯子的顶端沿墙下滑0.5m,梯子底端将外移0.58m.练习 1. 小明的妈妈买了一台29(74厘米)的电视机,小明量了电视机的荧屏后,发现荧屏只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?2. 如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m, AC =20m.你能求出A、B两点间的距离吗(结果保留整数)?
练习小结内容总结: 探索直角三角形两直角边的 平方和等于斜边的平方;利用勾股定理解决实际问题。方法总结: 用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形,再验证自己的发现。说说这节课你有什么收获? 勾股定理证
明应
用小
结练
习史
话猜
想作业 P77 习题1-4题,10题
再 见!
明应
用小
结猜
想练
习史
话观察思考 相传2500年前,毕达哥拉斯有一次在朋友家做客时,发现朋友家的用砖铺成的地面中反映了直角三角形三边的某种数量关系。同学们,我们也来观察下图中的地面,看看能发现些什么?
得出结论:
以等腰直角三角形两直角边为边长的小正方形的面积的和,等于以斜边为边长的正方形的面积.
即
在等腰直角三角形中,两直角边的平方和等于斜边的平方.一起探究 等腰直角三角形三边之间有上述性质,那么其他的直角三角形三边是否也具有上述性质呢?
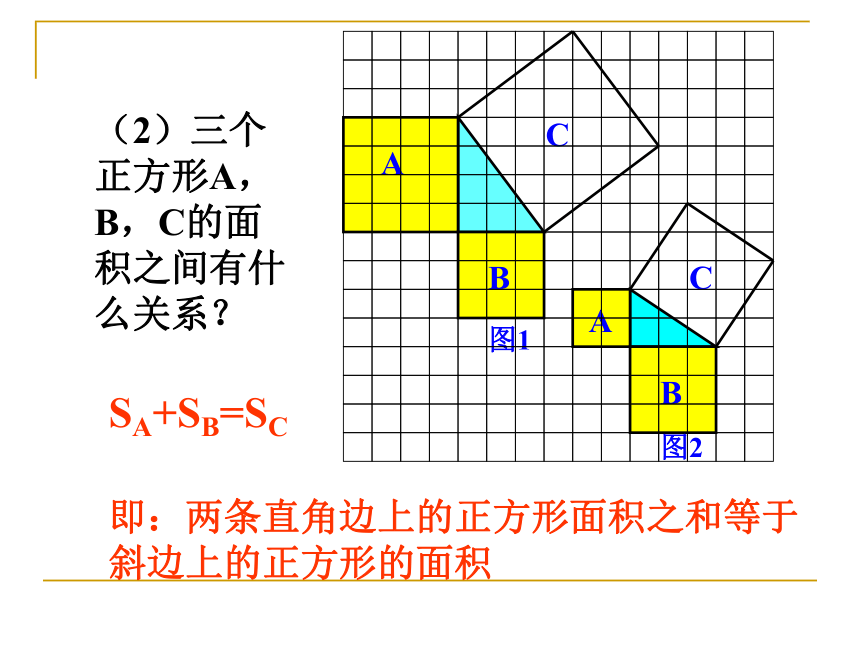
请用网格纸动手画一画,量一量,和同桌交流想法. C的面积(单位面积)1325(1)观察图1、图2,并填写下表: A的面积(单位面积) B的面积(单位面积) 图1 图216949做一做分割成若干个直角边为整数的三角形(面积单位)(2)三个正方形A,B,C的面积之间有什么关系?SA+SB=SC
即:两条直角边上的正方形面积之和等于 斜边上的正方形的面积 命题1 如果直角三角形的两直角边长分别为a、b,斜边长为c,那么: 猜想:左图的面积为 右图的面积为
a2+b2 c2
可知 a2+b2=C2
试一试 我国古代把直角三角形中较短的直角边称为勾,较长的直角边称为股,斜边称为弦.所以命题1叫勾股定理. 经过证明被确认正确的命题叫定理. 如果直角三角形的两直角边长分别为a、b,斜边长为c,那么: 勾a股b弦 c勾股定理(gou-gu theorem) 在中国古代大约是战国时期西汉的数学著作《周髀算经》中记录着商高同周公的一段对话。商高说:“…故折矩,勾广三,股修四,经隅五。”即:当直角三角形的两条直角边分别为3(短边)和4(长边)时,径隅(弦)则为5。以后人们就简单地把这个事实说成“勾三股四弦五”。故称之为“勾股定理”或“商高定理”史话勾股定理 在西方,希腊数学家欧几里德(Euclid,公元前三百年左右)在编著《几何原本》时,认为这个定理是毕达哥达斯最早发现的,所以他就把这个定理称为“毕达哥拉斯定理”,以后就流传开了。 毕达哥拉斯(Pythagoras)是古希腊数学家,他是公元前五世纪的人,比商高晚出生五百多年。 相传,毕达哥拉斯学派找到了勾股定理的证明后,欣喜若狂,杀了一百头牛祭神,由此,又有“百牛定理”之称。拓广应用1. 一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?分析:
连结AC,在Rt△ABC中,根据勾股定理:
因此,
因为AC大于木板的宽,所以木板能从门框内通过。拓广应用2.
一个3m长的梯子AB斜靠在一竖直的墙AC上,这时AC的距离为2.5m.如果梯子顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
分析:在Rt△ABC中,
在Rt△DCE中,
所以梯子的顶端沿墙下滑0.5m,梯子底端将外移0.58m.练习 1. 小明的妈妈买了一台29(74厘米)的电视机,小明量了电视机的荧屏后,发现荧屏只有58厘米长和46厘米宽,他觉得一定是售货员搞错了。你同意他的想法吗?你能解释这是为什么吗?2. 如图,池塘边有两点A、B,点C是与BA方向成直角的AC方向上一点,测得CB=60m, AC =20m.你能求出A、B两点间的距离吗(结果保留整数)?
练习小结内容总结: 探索直角三角形两直角边的 平方和等于斜边的平方;利用勾股定理解决实际问题。方法总结: 用直角三角形三边表示三个正方形面积——观察归纳发现勾股定理——任意画一个直角三角形,再验证自己的发现。说说这节课你有什么收获? 勾股定理证
明应
用小
结练
习史
话猜
想作业 P77 习题1-4题,10题
再 见!
