2023-2024学年初中数学人教版七年级下册5.3.1 平行线的性质 课时练习 (含答案)
文档属性
| 名称 | 2023-2024学年初中数学人教版七年级下册5.3.1 平行线的性质 课时练习 (含答案) | 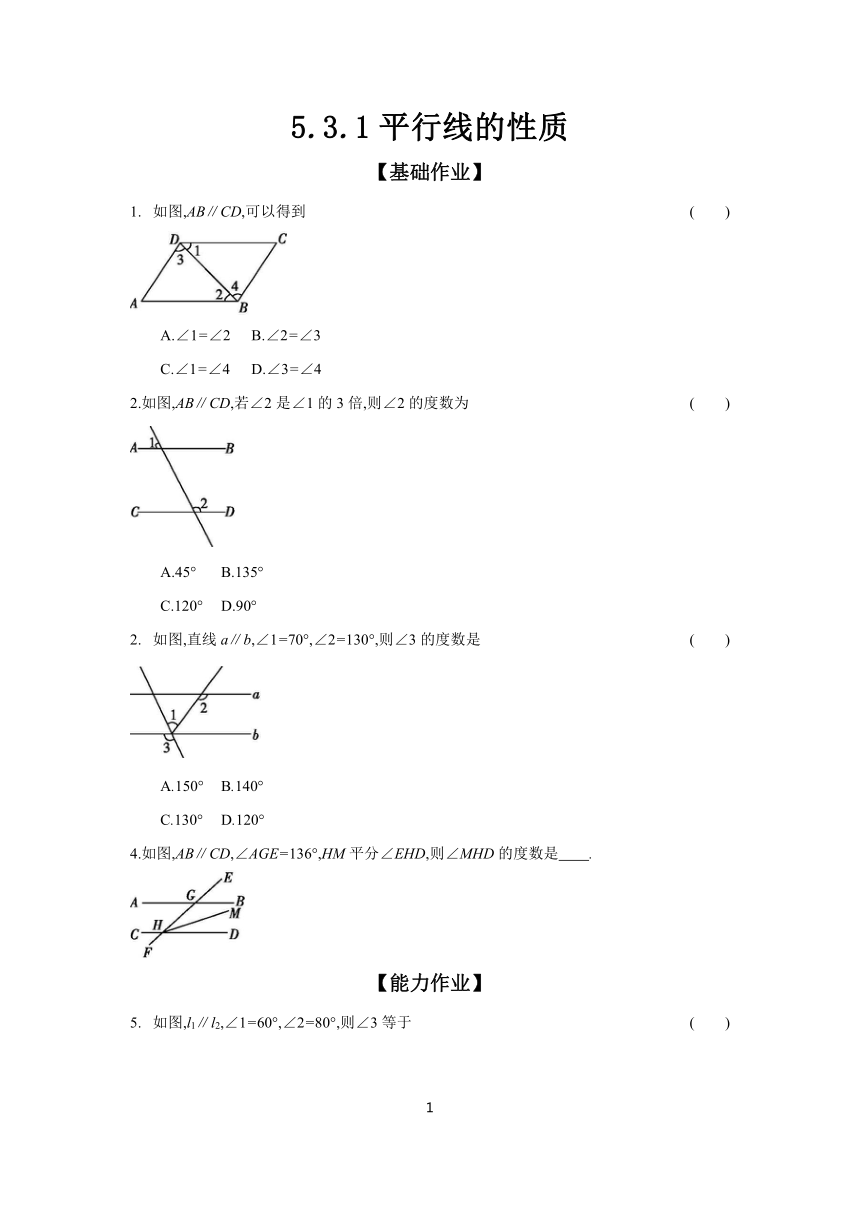 | |
| 格式 | docx | ||
| 文件大小 | 268.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 20:28:06 | ||
图片预览



文档简介
5.3.1平行线的性质
【基础作业】
如图,AB∥CD,可以得到 ( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
2.如图,AB∥CD,若∠2是∠1的3倍,则∠2的度数为 ( )
A.45° B.135°
C.120° D.90°
如图,直线a∥b,∠1=70°,∠2=130°,则∠3的度数是 ( )
A.150° B.140°
C.130° D.120°
4.如图,AB∥CD,∠AGE=136°,HM平分∠EHD,则∠MHD的度数是 .
【能力作业】
如图,l1∥l2,∠1=60°,∠2=80°,则∠3等于 ( )
A.10° B.20°
C.30° D.40°
如图,将对边平行的纸带按如图所示进行折叠,已知∠1=65°,则∠2的大小为 ( )
A.115° B.65°
C.55° D.50°
7.如图,AB∥CD,EF分别与AB、CD相交于点E,F,EP⊥EF,∠EFD的平分线FP与EP相交于点P,且∠BEP=40°,则∠EPF= .
8.如图,这是一张躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,当∠EOF=90°,∠ODC=30°时,人躺着最舒服,求此时扶手AB与支架OE的夹角∠AOE和扶手AB与靠背DM的夹角∠ANM的度数.
【素养作业】
9.如图,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,求∠BOF的度数.
10.如图,已知AB∥CD,试说明∠B+∠E=∠C+180°.
11.小聪把一副三角尺ABC,DCE按图1所示的方式摆放,其中边BC,DC在同一条直线上,如图2,过点A向右作射线AP∥DE.(∠ABC=∠DCE=90°,∠E=60°,∠D=30°,∠BAC=∠ACB=45°)
(1)求∠PAC的度数.
(2)如图3,Q是线段BC上一点,若∠AQB=∠PAQ,求∠QAB的度数.
参考答案
1.A 2.B 3.D
4.22° 5.B 6.D 7.65°
8.解:∵扶手AB与底座CD都平行于地面,
∴AB∥CD,
∴∠ODC=∠BOD=30°.
又∵∠EOF=90°,
∴∠AOE=60°.
∵DM∥OE,
∴∠AND=∠AOE=60°,
∴∠ANM=180°-∠AND=120°.
9.解:∵CD∥AB,∴∠D+∠AOD=180°.∵∠D=50°,∴∠AOD=130°.
∵OE平分∠AOD,∴∠EOA=65°.∵OF⊥OE,
∴∠EOF=90°,∴∠AOF=155°,∴∠BOF=25°.
10.解:如图,过点E作直线EF,使得EF∥AB.
∵EF∥AB,
∴∠B+∠BEF=180°(两直线平行,同旁内角互补).
又∵AB∥CD,
∴EF∥CD(平行于同一直线的两条直线平行),
∴∠FEC=∠C(两直线平行,内错角相等).
∵∠BEC=∠BEF+∠FEC,
∴∠B+∠BEC=∠B+∠BEF+∠FEC,
故∠B+∠BEC=180°+∠C(等量代换).
11.解:(1)∵AP∥DE,
易得∠PAB+∠D=∠ABD.
∵∠D=30°,∠ABD=90°,∠BAC=45°,
∴∠PAC=15°.
(2)∵AP∥DE,
易得∠PAQ+∠D=∠AQB.
∵∠AQB=∠PAQ,
设∠PAQ=x,则∠AQB=x,
∴x+30°=x,
解得x=45°,
由(1)可知∠PAB=∠BAC+∠PAC=45°+15°=60°,
∴∠QAB=∠PAB-∠PAQ=60°-45°=15°.
2
【基础作业】
如图,AB∥CD,可以得到 ( )
A.∠1=∠2 B.∠2=∠3
C.∠1=∠4 D.∠3=∠4
2.如图,AB∥CD,若∠2是∠1的3倍,则∠2的度数为 ( )
A.45° B.135°
C.120° D.90°
如图,直线a∥b,∠1=70°,∠2=130°,则∠3的度数是 ( )
A.150° B.140°
C.130° D.120°
4.如图,AB∥CD,∠AGE=136°,HM平分∠EHD,则∠MHD的度数是 .
【能力作业】
如图,l1∥l2,∠1=60°,∠2=80°,则∠3等于 ( )
A.10° B.20°
C.30° D.40°
如图,将对边平行的纸带按如图所示进行折叠,已知∠1=65°,则∠2的大小为 ( )
A.115° B.65°
C.55° D.50°
7.如图,AB∥CD,EF分别与AB、CD相交于点E,F,EP⊥EF,∠EFD的平分线FP与EP相交于点P,且∠BEP=40°,则∠EPF= .
8.如图,这是一张躺椅及其简化结构示意图,扶手AB与底座CD都平行于地面,靠背DM与支架OE平行,前支架OE与后支架OF分别与CD交于点G和点D,AB与DM交于点N,当∠EOF=90°,∠ODC=30°时,人躺着最舒服,求此时扶手AB与支架OE的夹角∠AOE和扶手AB与靠背DM的夹角∠ANM的度数.
【素养作业】
9.如图,CD∥AB,OE平分∠AOD,OF⊥OE,∠D=50°,求∠BOF的度数.
10.如图,已知AB∥CD,试说明∠B+∠E=∠C+180°.
11.小聪把一副三角尺ABC,DCE按图1所示的方式摆放,其中边BC,DC在同一条直线上,如图2,过点A向右作射线AP∥DE.(∠ABC=∠DCE=90°,∠E=60°,∠D=30°,∠BAC=∠ACB=45°)
(1)求∠PAC的度数.
(2)如图3,Q是线段BC上一点,若∠AQB=∠PAQ,求∠QAB的度数.
参考答案
1.A 2.B 3.D
4.22° 5.B 6.D 7.65°
8.解:∵扶手AB与底座CD都平行于地面,
∴AB∥CD,
∴∠ODC=∠BOD=30°.
又∵∠EOF=90°,
∴∠AOE=60°.
∵DM∥OE,
∴∠AND=∠AOE=60°,
∴∠ANM=180°-∠AND=120°.
9.解:∵CD∥AB,∴∠D+∠AOD=180°.∵∠D=50°,∴∠AOD=130°.
∵OE平分∠AOD,∴∠EOA=65°.∵OF⊥OE,
∴∠EOF=90°,∴∠AOF=155°,∴∠BOF=25°.
10.解:如图,过点E作直线EF,使得EF∥AB.
∵EF∥AB,
∴∠B+∠BEF=180°(两直线平行,同旁内角互补).
又∵AB∥CD,
∴EF∥CD(平行于同一直线的两条直线平行),
∴∠FEC=∠C(两直线平行,内错角相等).
∵∠BEC=∠BEF+∠FEC,
∴∠B+∠BEC=∠B+∠BEF+∠FEC,
故∠B+∠BEC=180°+∠C(等量代换).
11.解:(1)∵AP∥DE,
易得∠PAB+∠D=∠ABD.
∵∠D=30°,∠ABD=90°,∠BAC=45°,
∴∠PAC=15°.
(2)∵AP∥DE,
易得∠PAQ+∠D=∠AQB.
∵∠AQB=∠PAQ,
设∠PAQ=x,则∠AQB=x,
∴x+30°=x,
解得x=45°,
由(1)可知∠PAB=∠BAC+∠PAC=45°+15°=60°,
∴∠QAB=∠PAB-∠PAQ=60°-45°=15°.
2
