第五章 相交线与平行线 复习课 课时练习 (含答案)2023-2024学年初中数学人教版七年级下册
文档属性
| 名称 | 第五章 相交线与平行线 复习课 课时练习 (含答案)2023-2024学年初中数学人教版七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 285.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 21:09:54 | ||
图片预览



文档简介
第五章 相交线与平行线 复习课
【基础作业】
如图,若∠AOC增大50°,则∠BOD ( )
A.减少50° B.不变
C.增大50° D.增大130°
2.如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,则∠3的度数为 ( )
A.40° B.50° C.60° D.70°
3.如图,给出了过直线外一点画已知直线的平行线的方法,其依据是 ( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
4.如图,在铁路旁边有一李庄,现要建一个火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),理由: .
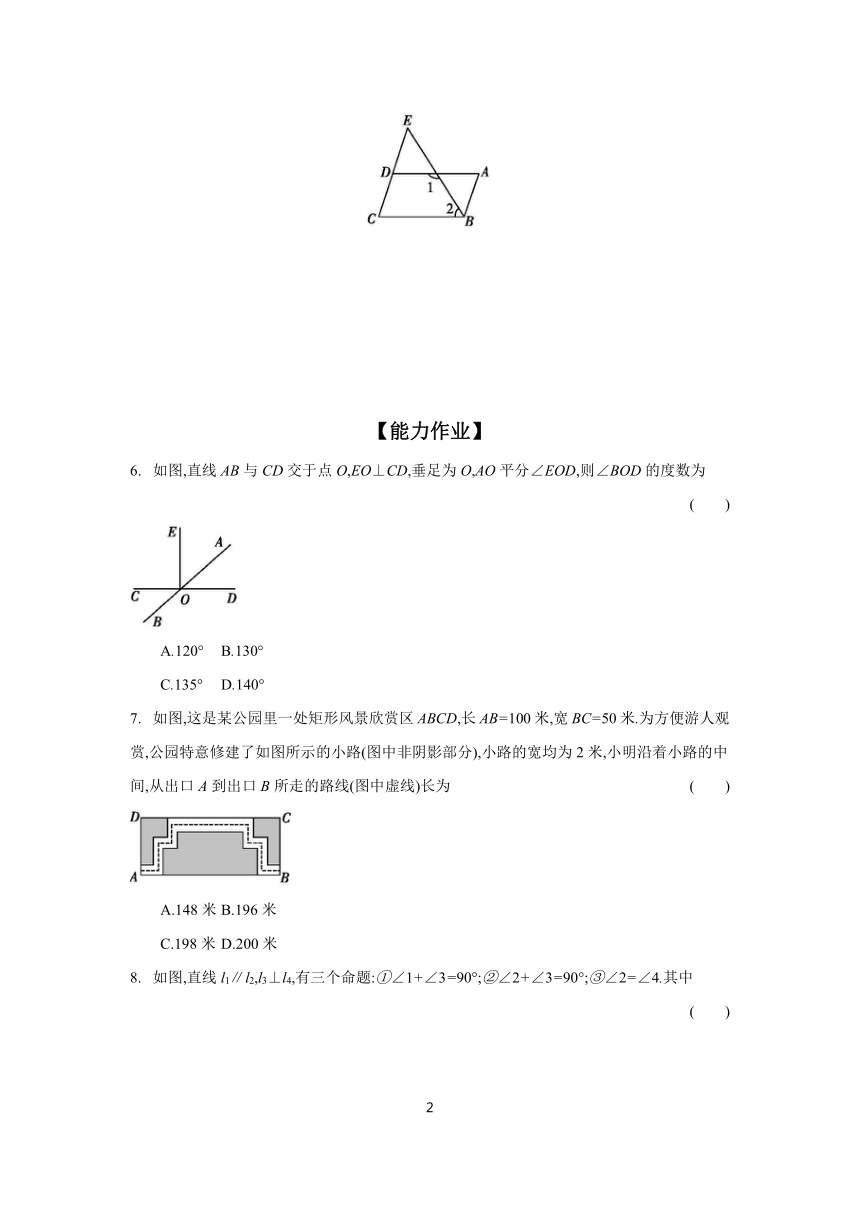
5.如图,已知∠A=∠C,∠1=125°,∠2=55°,试猜想AB与CD之间有怎样的位置关系 并说明理由.
【能力作业】
如图,直线AB与CD交于点O,EO⊥CD,垂足为O,AO平分∠EOD,则∠BOD的度数为 ( )
A.120° B.130°
C.135° D.140°
如图,这是某公园里一处矩形风景欣赏区ABCD,长AB=100米,宽BC=50米.为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为2米,小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为 ( )
A.148米 B.196米
C.198米 D.200米
如图,直线l1∥l2,l3⊥l4,有三个命题:①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4.其中 ( )
A.只有①正确 B.只有②正确
C.①和③正确 D.①②③都正确
9.如图,一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为 ( )
A.45° B.60° C.75° D.80°
10.平移变换不仅和几何图形密切联系,在汉字中也存在着平移变换现象,如:“林”“田”“众”.请你开动脑筋,写出三个可由平移变换得到的汉字: .
11.要说明命题“互补的角是同旁内角”是假命题,可举反例 .
12.如图,∠ADE=∠B,∠1+∠2=180°,CD⊥AB,请填写理由,说明GF⊥AB.
13.如图,为了解决A、B、C、D四个小区的缺水问题,市政府准备投资修建一个水厂.
(1)不考虑其他因素,请你画图确定水厂H的位置,使之与四个小区的距离之和最小.
(2)另外,计划把河流EF中的水引入水厂H中,使之到H的距离最短,请你画图确定铺设引水管道的位置,并说明理由.
14.如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=30°,求∠BOE及∠AOG的度数.
【素养作业】
15.将一副三角板中的两块直角三角尺的直角顶点C按如图1的方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.
(1)若∠1=25°,则∠2的度数为 .
(2)∠1与∠3的数量关系为 .
(3)∠2与∠ACB的数量关系为 .
(4)如图2,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两块三角尺的顶点C重合,∠ACE<180°且点E在直线AC的上方,这两块三角尺是否存在一组边互相平行 请直接写出∠ACE所有可能的值.
参考答案
1.C 2.D 3.A
4.垂线段最短
5解:AB∥CD.
理由:∵∠1=125°,∠2=55°,
∴∠1+∠2=180°,
∴AD∥BC,
∴∠C=∠EDA.
∵∠A=∠C,
∴∠A=∠EDA,
∴AB∥CD.
6.C 7.B 8.A 9.A
10.答案不唯一,如羽、朋、圭
11.答案不唯一,如邻补角互补,但它们不是同旁内角
12.同位角相等,两直线平行 两直线平行,内错角相等 等量代换 CD FG 同旁内角互补,两直线平行 两直线平行,同位角相等
13.解:(1)如图,连接AC、BD交于点H,则点H即为修建水厂的位置.
(2)如图,过点H作HG⊥EF,垂足为G,则沿HG铺设引水管道,可满足题意,理由:垂线段最短.
14.解:∵∠FOD=30°,∠COE与∠FOD是对顶角,
∴∠EOC=30°.
∵AB⊥CD,
∴∠BOC=90°,∠BOE=∠BOC-∠EOC=60°.
∵∠AOE=90°+∠EOC=120°且OG平分∠AOE,
∴∠AOG=60°.
15.解:(1)65°.
(2)∵∠1+∠2=∠ACD=90°,∠2+∠3=∠BCE=90°,
∴∠1+∠2=∠2+∠3,
∴∠1=∠3,
故答案为∠1=∠3.
(3)∵∠ACD=∠BCE=90°,
∴∠ACB+∠2
=∠1+∠2+∠3+∠2
=∠ACD+∠BCE
=180°,
即∠2+∠ACB=180°,
故答案为∠2+∠ACB=180°.
(4)存在.
①当BC∥AD时,∠BCD=∠D=30°,
∴∠ACB=90°+30°=120°,
∴
∠ACE=∠ACB-∠BCE=120°-90°=30°;
②当BE∥AC时,如图1,∠ACE=∠E=45°;
③当AD∥CE时,如图2,∠DCE=∠D=30°,
∴∠ACE=90°+30°=120°;
④当BE∥CD时,如图3,
∠DCE=∠E=45°,
∴∠ACE=∠ACD+∠DCE=135°;
⑤当BE∥AD时,如图4,
过点C作CF∥AD,∴BE∥AD∥CF,
∴∠ECF=∠E=45°,∠DCF=∠D=30°,
∴∠DCE=30°+45°=75°,
∴∠ACE=90°+75°=165°.
综上所述,当∠ACE为30°或45°或120°或135°或165°时,有一组边互相平行.
2
【基础作业】
如图,若∠AOC增大50°,则∠BOD ( )
A.减少50° B.不变
C.增大50° D.增大130°
2.如图,直线AC和直线BD相交于点O,OE平分∠BOC.若∠1+∠2=80°,则∠3的度数为 ( )
A.40° B.50° C.60° D.70°
3.如图,给出了过直线外一点画已知直线的平行线的方法,其依据是 ( )
A.同位角相等,两直线平行
B.内错角相等,两直线平行
C.同旁内角互补,两直线平行
D.两直线平行,同位角相等
4.如图,在铁路旁边有一李庄,现要建一个火车站,为了使李庄人乘火车最方便(即距离最近),请你在铁路旁选一点来建火车站(位置已选好),理由: .
5.如图,已知∠A=∠C,∠1=125°,∠2=55°,试猜想AB与CD之间有怎样的位置关系 并说明理由.
【能力作业】
如图,直线AB与CD交于点O,EO⊥CD,垂足为O,AO平分∠EOD,则∠BOD的度数为 ( )
A.120° B.130°
C.135° D.140°
如图,这是某公园里一处矩形风景欣赏区ABCD,长AB=100米,宽BC=50米.为方便游人观赏,公园特意修建了如图所示的小路(图中非阴影部分),小路的宽均为2米,小明沿着小路的中间,从出口A到出口B所走的路线(图中虚线)长为 ( )
A.148米 B.196米
C.198米 D.200米
如图,直线l1∥l2,l3⊥l4,有三个命题:①∠1+∠3=90°;②∠2+∠3=90°;③∠2=∠4.其中 ( )
A.只有①正确 B.只有②正确
C.①和③正确 D.①②③都正确
9.如图,一束光线垂直照射水平地面,在地面上放一个平面镜,欲使这束光线经平面镜反射后成水平光线,则平面镜与地面所成锐角的度数为 ( )
A.45° B.60° C.75° D.80°
10.平移变换不仅和几何图形密切联系,在汉字中也存在着平移变换现象,如:“林”“田”“众”.请你开动脑筋,写出三个可由平移变换得到的汉字: .
11.要说明命题“互补的角是同旁内角”是假命题,可举反例 .
12.如图,∠ADE=∠B,∠1+∠2=180°,CD⊥AB,请填写理由,说明GF⊥AB.
13.如图,为了解决A、B、C、D四个小区的缺水问题,市政府准备投资修建一个水厂.
(1)不考虑其他因素,请你画图确定水厂H的位置,使之与四个小区的距离之和最小.
(2)另外,计划把河流EF中的水引入水厂H中,使之到H的距离最短,请你画图确定铺设引水管道的位置,并说明理由.
14.如图,直线AB、CD、EF相交于点O,AB⊥CD,OG平分∠AOE,∠FOD=30°,求∠BOE及∠AOG的度数.
【素养作业】
15.将一副三角板中的两块直角三角尺的直角顶点C按如图1的方式叠放在一起,其中∠A=60°,∠D=30°,∠E=∠B=45°.
(1)若∠1=25°,则∠2的度数为 .
(2)∠1与∠3的数量关系为 .
(3)∠2与∠ACB的数量关系为 .
(4)如图2,将三角尺ACD固定不动,改变三角尺BCE的位置,但始终保持两块三角尺的顶点C重合,∠ACE<180°且点E在直线AC的上方,这两块三角尺是否存在一组边互相平行 请直接写出∠ACE所有可能的值.
参考答案
1.C 2.D 3.A
4.垂线段最短
5解:AB∥CD.
理由:∵∠1=125°,∠2=55°,
∴∠1+∠2=180°,
∴AD∥BC,
∴∠C=∠EDA.
∵∠A=∠C,
∴∠A=∠EDA,
∴AB∥CD.
6.C 7.B 8.A 9.A
10.答案不唯一,如羽、朋、圭
11.答案不唯一,如邻补角互补,但它们不是同旁内角
12.同位角相等,两直线平行 两直线平行,内错角相等 等量代换 CD FG 同旁内角互补,两直线平行 两直线平行,同位角相等
13.解:(1)如图,连接AC、BD交于点H,则点H即为修建水厂的位置.
(2)如图,过点H作HG⊥EF,垂足为G,则沿HG铺设引水管道,可满足题意,理由:垂线段最短.
14.解:∵∠FOD=30°,∠COE与∠FOD是对顶角,
∴∠EOC=30°.
∵AB⊥CD,
∴∠BOC=90°,∠BOE=∠BOC-∠EOC=60°.
∵∠AOE=90°+∠EOC=120°且OG平分∠AOE,
∴∠AOG=60°.
15.解:(1)65°.
(2)∵∠1+∠2=∠ACD=90°,∠2+∠3=∠BCE=90°,
∴∠1+∠2=∠2+∠3,
∴∠1=∠3,
故答案为∠1=∠3.
(3)∵∠ACD=∠BCE=90°,
∴∠ACB+∠2
=∠1+∠2+∠3+∠2
=∠ACD+∠BCE
=180°,
即∠2+∠ACB=180°,
故答案为∠2+∠ACB=180°.
(4)存在.
①当BC∥AD时,∠BCD=∠D=30°,
∴∠ACB=90°+30°=120°,
∴
∠ACE=∠ACB-∠BCE=120°-90°=30°;
②当BE∥AC时,如图1,∠ACE=∠E=45°;
③当AD∥CE时,如图2,∠DCE=∠D=30°,
∴∠ACE=90°+30°=120°;
④当BE∥CD时,如图3,
∠DCE=∠E=45°,
∴∠ACE=∠ACD+∠DCE=135°;
⑤当BE∥AD时,如图4,
过点C作CF∥AD,∴BE∥AD∥CF,
∴∠ECF=∠E=45°,∠DCF=∠D=30°,
∴∠DCE=30°+45°=75°,
∴∠ACE=90°+75°=165°.
综上所述,当∠ACE为30°或45°或120°或135°或165°时,有一组边互相平行.
2
