6.4 多边形的内角和与外角和 课件(共26张PPT)
文档属性
| 名称 | 6.4 多边形的内角和与外角和 课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-29 08:36:00 | ||
图片预览







文档简介
(共26张PPT)
第6章 平行四边形
6.4 多边形的内角和与外角和
1.掌握多边形内角和定理与外角和定理,进一步了解转化的数学思想
2.经历质疑、猜想、归纳等活动,发展学生的合情推理能力
1.多边形内角和、外角和定理的探索和应用
2.多边形定义的理解;多边形内角和公式的推导
教学目标
重难点
导入新课
三角形是如何定义的?
三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形.
仿照三角形定义,你能学着给四边形.五边形……n边形下定义吗?
学习新知
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形.
.
.
.
.
.
顶点
对角线
边
内角
外角
探究新知
问题2 你知道长方形和正方形的内角和是多少度?
问题1 三角形的内角和是多少度?
三角形内角和是180°.
都是 360°.
问题3 猜想任意四边形的内角和是多少度.
探究新知
健身广场中心的边缘是一个五边形(如图),你能类比求四边形内角和的方法求出它的五个内角的和吗?
探究新知
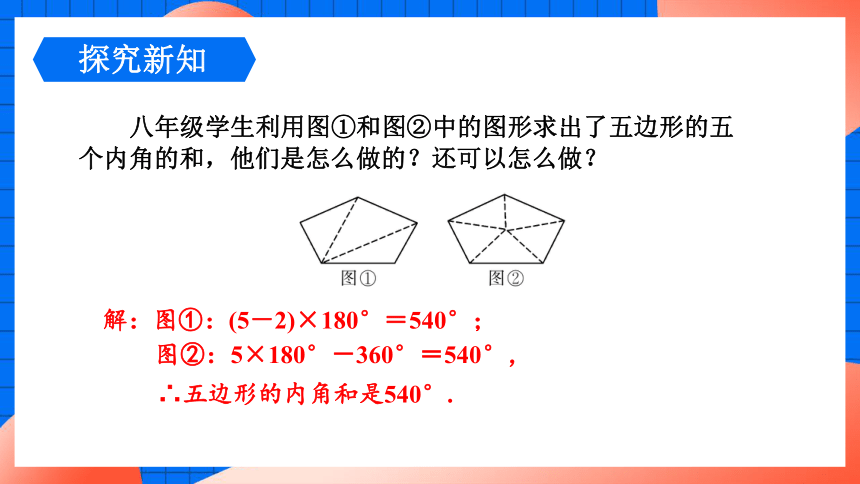
八年级学生利用图①和图②中的图形求出了五边形的五个内角的和,他们是怎么做的?还可以怎么做?
解:图①:(5-2)×180°=540°;
图②:5×180°-360°=540°,
∴五边形的内角和是540°.
探究新知
按照上边的方法,六边形能分成多少个三角形?n边形呢?你能确定n边形的内角和吗?
4个
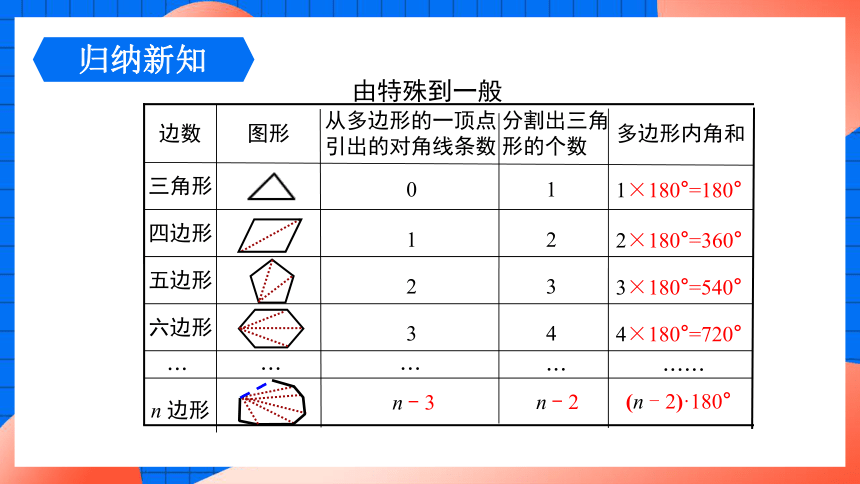
归纳新知
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
···
0
n - 3
1
2
3
1
2
3
4
n - 2
(n - 2)·180°
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
···
···
······
···
由特殊到一般
归纳小结
从n边形的一个顶点可以引出(n-3)条对角线,把n边形分成(n-2)个三角形.从而得出多边形内角和定理:n边形的内角和等于(n-2)·180°.
小牛试刀
1.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成7个三角形,则n的值是( )
A.6 B.7 C.8 D.9
2.从n边形的一个顶点出发可以连接6条对角线,则n的值为( )
A.8 B.9 C.10 D.11
D
B
典型例题
例.如图,四边形ABCD中,已知∠ABC,∠BCD的平分线相交于点O,∠A+∠D=200°,求∠BOC的度数.
【分析】由四边形的内角和为(4-2)×180°=360°,可求出∠ABC+∠BCD的度数,进而根据题目条件转化到△BOC中,利用三角形内角和定理求出∠BOC的大小.
典型例题
解:在四边形ABCD中,∠A+∠ABC+∠BCD+∠D=360°.
∵∠BOC+∠OBC+∠OCB=180°,
∵∠A+∠D=200°,
∴∠ABC+∠BCD=360°-200°=160°.
∵BO,CO分别是∠ABC,∠BCD的平分线,
∴∠OBC= ∠ABC,∠OCB= ∠BCD,
∴∠OBC+∠OCB= (∠ABC+∠BCD)= ×160°=80°.
∴∠BOC=180°-80°=100°.
即∠BOC的度数为100°.
探究新知
如图,小刚每跑完一圈,身体转过的角度之和是多少?
探究新知
小刚是这样思考的:如图,跑步方向改变的角分别是∠1,∠2,∠3,∠4,∠5.
学习新知
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
如图,∠A 的外角是∠1.
E
B
C
D
1
2
3
4
5
A
在多边形每个顶点处各取一个外角,它们的和叫做这个多边形的外角和.
探究新知
∵∠1+∠EAB=180°,∠2+∠ABC=180°,
∠3+∠BCD=180°,∠4+∠CDE=180°,
∠5+∠DEA=180°,
∴∠1+∠EAB+∠2+∠ABC+∠3+∠BCD+
∠4+∠CDE+∠5+∠DEA=900°
∵五边形的内角和为(5-2)×180°=540°,
即∠EAB+∠ABC+∠BCD+∠CDE+∠DEA=540°
∴∠1+∠2+∠3+∠4+∠5=360°
探究新知
n 边形的外角和
n 边形的外角和等于 360°.
-(n-2) × 180°
= 360°.
= n 个平角- n 边形的内角和
= n×180°
An
A2
A3
A4
1
2
3
4
n
A1
思考:n 边形的外角和又是多少呢?
与边数无关
探究新知
思考:回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:(1) 若一个正多边形的内角是 120°,那么这是
正____边形.
(2) 已知某正多边形的每个外角都是 45°,则这个多边形
是______边形.
六
正八
随堂练习
1.一个多边形的边数是12,这个多边形的内角和是
( )
A.1 800° B.1 440°
C.1 980° D.540°
2.一个多边形的内角和等于1 080°,则它的边数是
( )
A.5 B.6 C.8 D.12
A
C
随堂练习
3.下列角度不可能是多边形的内角和的是( )
A.1 260° B.960° C.1 440° D.540°
4.若一个正多边形的每一个内角都是150°,这个正多边形的边数是______.
12
B
随堂练习
5.内角和等于外角和2倍的多边形是( )
A.五边形 B.六边形
C.七边形 D.八边形
6.六边形的内角和等于______度.
7.正十边形的每一个内角的度数等于______,每一个外角的度数等于______.
B
720
144°
36°
随堂练习
8. 一个多边形的内角和为 1800°,截去一个角后,求得到的多边形的内角和.
解:∵ 1800÷180 = 10,
∴ 原多边形边数为10+2 = 12.
∵ 一个多边形截去一个内角后,边数可能减 1,可能不变,也可能加 1,
即新多边形的边数可能是 11,12,13,
∴ 新多边形的内角和可能是 1620°,1800°,1980°.
课堂小结
多边形的内角和
内角和计算公式
(n - 2) ×180°(n≥3的整数)
外角和
多边形的外角和等于 360°.
特别注意:与边数无关.
正多
边形
内角= ,外角=
课后作业
完成教材习题6.7
这节课你学到了什么?谈谈你的收获,
小结与反思
第6章 平行四边形
6.4 多边形的内角和与外角和
1.掌握多边形内角和定理与外角和定理,进一步了解转化的数学思想
2.经历质疑、猜想、归纳等活动,发展学生的合情推理能力
1.多边形内角和、外角和定理的探索和应用
2.多边形定义的理解;多边形内角和公式的推导
教学目标
重难点
导入新课
三角形是如何定义的?
三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形.
仿照三角形定义,你能学着给四边形.五边形……n边形下定义吗?
学习新知
在平面内,由若干不在同一直线上的线段首尾顺次连接组成的封闭图形叫做多边形.
.
.
.
.
.
顶点
对角线
边
内角
外角
探究新知
问题2 你知道长方形和正方形的内角和是多少度?
问题1 三角形的内角和是多少度?
三角形内角和是180°.
都是 360°.
问题3 猜想任意四边形的内角和是多少度.
探究新知
健身广场中心的边缘是一个五边形(如图),你能类比求四边形内角和的方法求出它的五个内角的和吗?
探究新知
八年级学生利用图①和图②中的图形求出了五边形的五个内角的和,他们是怎么做的?还可以怎么做?
解:图①:(5-2)×180°=540°;
图②:5×180°-360°=540°,
∴五边形的内角和是540°.
探究新知
按照上边的方法,六边形能分成多少个三角形?n边形呢?你能确定n边形的内角和吗?
4个
归纳新知
n 边形
六边形
五边形
四边形
三角形
多边形内角和
分割出三角形的个数
从多边形的一顶点引出的对角线条数
图形
边数
···
0
n - 3
1
2
3
1
2
3
4
n - 2
(n - 2)·180°
1×180°=180°
2×180°=360°
3×180°=540°
4×180°=720°
···
···
······
···
由特殊到一般
归纳小结
从n边形的一个顶点可以引出(n-3)条对角线,把n边形分成(n-2)个三角形.从而得出多边形内角和定理:n边形的内角和等于(n-2)·180°.
小牛试刀
1.从一个n边形的同一个顶点出发,分别连接这个顶点与其余各顶点,若把这个多边形分割成7个三角形,则n的值是( )
A.6 B.7 C.8 D.9
2.从n边形的一个顶点出发可以连接6条对角线,则n的值为( )
A.8 B.9 C.10 D.11
D
B
典型例题
例.如图,四边形ABCD中,已知∠ABC,∠BCD的平分线相交于点O,∠A+∠D=200°,求∠BOC的度数.
【分析】由四边形的内角和为(4-2)×180°=360°,可求出∠ABC+∠BCD的度数,进而根据题目条件转化到△BOC中,利用三角形内角和定理求出∠BOC的大小.
典型例题
解:在四边形ABCD中,∠A+∠ABC+∠BCD+∠D=360°.
∵∠BOC+∠OBC+∠OCB=180°,
∵∠A+∠D=200°,
∴∠ABC+∠BCD=360°-200°=160°.
∵BO,CO分别是∠ABC,∠BCD的平分线,
∴∠OBC= ∠ABC,∠OCB= ∠BCD,
∴∠OBC+∠OCB= (∠ABC+∠BCD)= ×160°=80°.
∴∠BOC=180°-80°=100°.
即∠BOC的度数为100°.
探究新知
如图,小刚每跑完一圈,身体转过的角度之和是多少?
探究新知
小刚是这样思考的:如图,跑步方向改变的角分别是∠1,∠2,∠3,∠4,∠5.
学习新知
多边形内角的一边与另一边的反向延长线所组成的角叫做这个多边形的外角.
如图,∠A 的外角是∠1.
E
B
C
D
1
2
3
4
5
A
在多边形每个顶点处各取一个外角,它们的和叫做这个多边形的外角和.
探究新知
∵∠1+∠EAB=180°,∠2+∠ABC=180°,
∠3+∠BCD=180°,∠4+∠CDE=180°,
∠5+∠DEA=180°,
∴∠1+∠EAB+∠2+∠ABC+∠3+∠BCD+
∠4+∠CDE+∠5+∠DEA=900°
∵五边形的内角和为(5-2)×180°=540°,
即∠EAB+∠ABC+∠BCD+∠CDE+∠DEA=540°
∴∠1+∠2+∠3+∠4+∠5=360°
探究新知
n 边形的外角和
n 边形的外角和等于 360°.
-(n-2) × 180°
= 360°.
= n 个平角- n 边形的内角和
= n×180°
An
A2
A3
A4
1
2
3
4
n
A1
思考:n 边形的外角和又是多少呢?
与边数无关
探究新知
思考:回想正多边形的性质,你知道正多边形的每个内角是多少度吗?每个外角呢?为什么?
每个内角的度数是
每个外角的度数是
练一练:(1) 若一个正多边形的内角是 120°,那么这是
正____边形.
(2) 已知某正多边形的每个外角都是 45°,则这个多边形
是______边形.
六
正八
随堂练习
1.一个多边形的边数是12,这个多边形的内角和是
( )
A.1 800° B.1 440°
C.1 980° D.540°
2.一个多边形的内角和等于1 080°,则它的边数是
( )
A.5 B.6 C.8 D.12
A
C
随堂练习
3.下列角度不可能是多边形的内角和的是( )
A.1 260° B.960° C.1 440° D.540°
4.若一个正多边形的每一个内角都是150°,这个正多边形的边数是______.
12
B
随堂练习
5.内角和等于外角和2倍的多边形是( )
A.五边形 B.六边形
C.七边形 D.八边形
6.六边形的内角和等于______度.
7.正十边形的每一个内角的度数等于______,每一个外角的度数等于______.
B
720
144°
36°
随堂练习
8. 一个多边形的内角和为 1800°,截去一个角后,求得到的多边形的内角和.
解:∵ 1800÷180 = 10,
∴ 原多边形边数为10+2 = 12.
∵ 一个多边形截去一个内角后,边数可能减 1,可能不变,也可能加 1,
即新多边形的边数可能是 11,12,13,
∴ 新多边形的内角和可能是 1620°,1800°,1980°.
课堂小结
多边形的内角和
内角和计算公式
(n - 2) ×180°(n≥3的整数)
外角和
多边形的外角和等于 360°.
特别注意:与边数无关.
正多
边形
内角= ,外角=
课后作业
完成教材习题6.7
这节课你学到了什么?谈谈你的收获,
小结与反思
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
