间接证明(反证法)
图片预览



文档简介
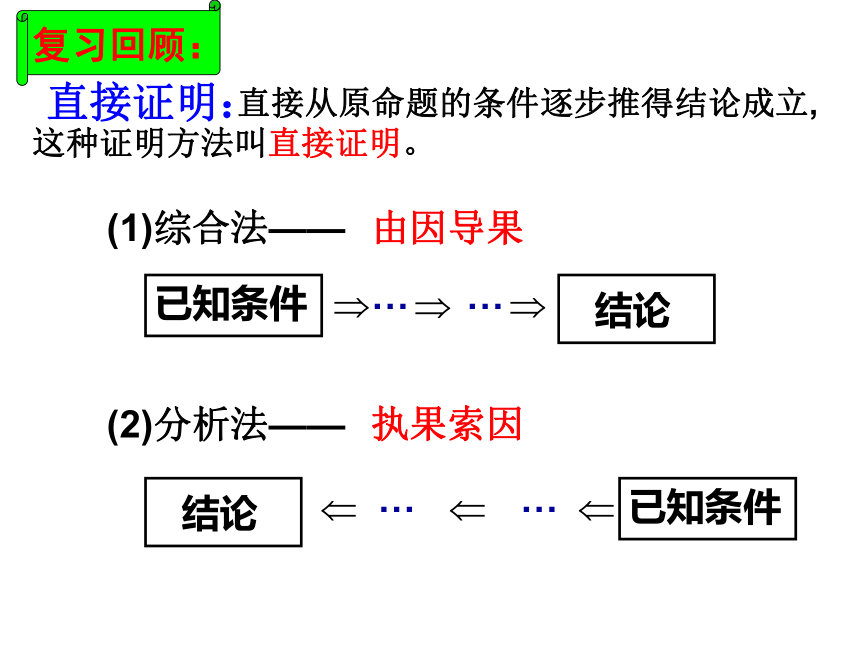
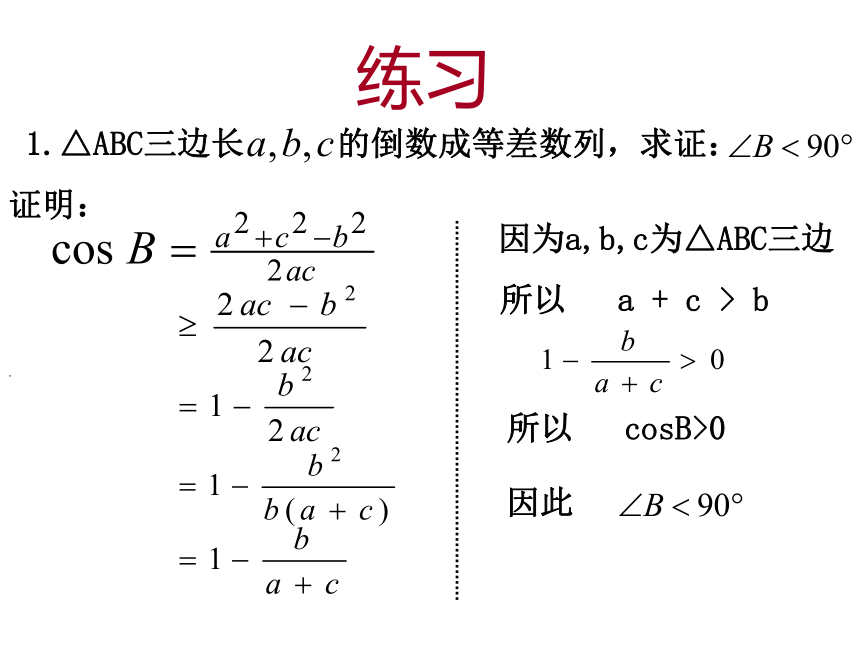
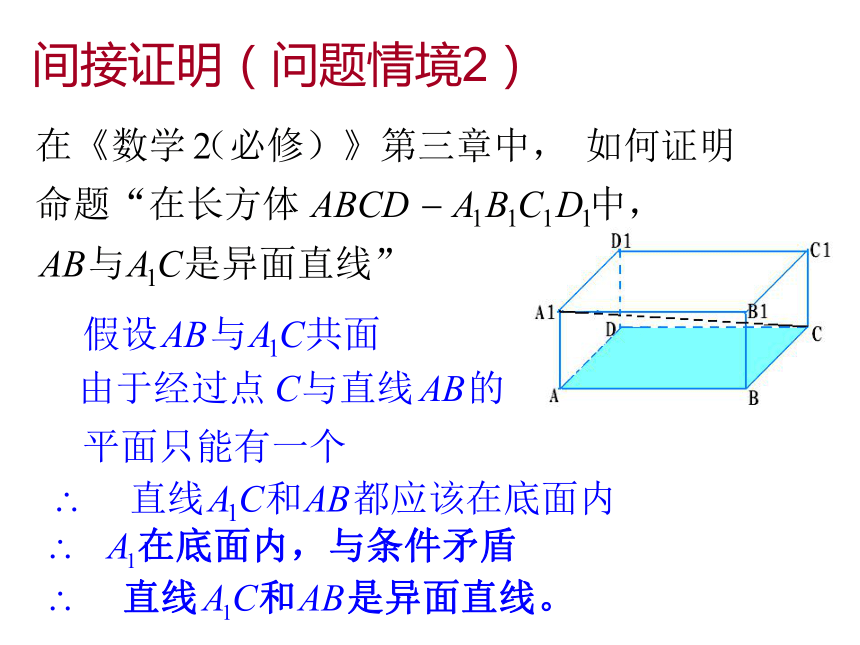
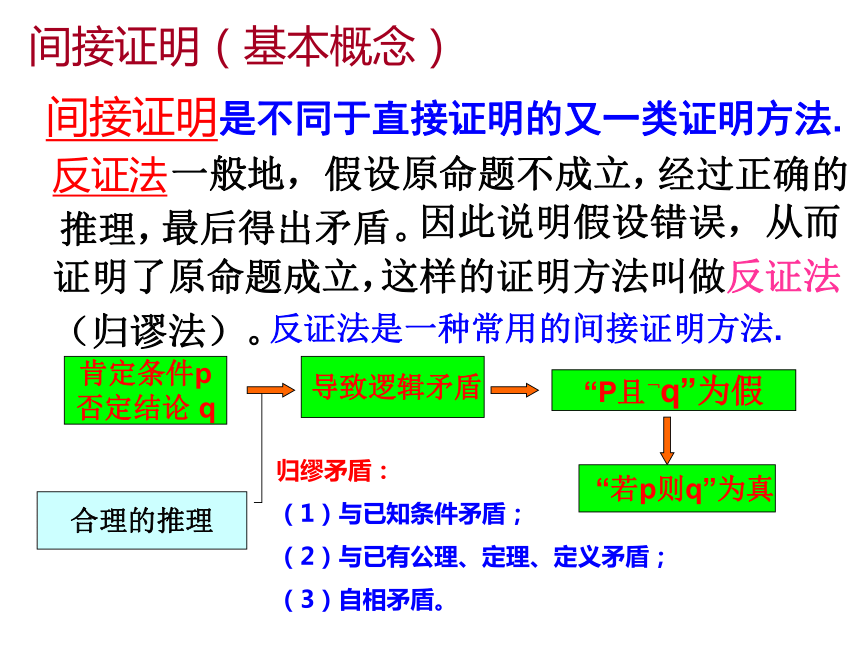
课件17张PPT。直接证明:(1)综合法——(2)分析法——由因导果执果索因 直接从原命题的条件逐步推得结论成立,这种证明方法叫直接证明。复习回顾:练习1.△ABC三边长的倒数成等差数列,求证:. 证明:因为a,b,c为△ABC三边 所以 a + c > b 所以 cosB>0 因此间接证明反证法 A、B、C三个人,A说B撒谎,B说C撒谎,C说A、B都撒谎。则C必定是在撒谎,为什么?分析:假设C没有撒谎, 则C真. - - 那么A假且B假;由A假, 知B真. 这与B假矛盾.那么假设C没有撒谎不成立,则C必定是在撒谎.间接证明(问题情境1)间接证明(问题情境2)间接证明(基本概念)间接证明是不同于直接证明的又一类证明方法.反证法 经过正确的推理, 因此说明假设错误,从而证明了原命题成立, 这样的证明方法叫做反证法(归谬法)。 一般地,假设原命题不成立,最后得出矛盾。反证法是一种常用的间接证明方法.肯定条件p
否定结论 q 导致逻辑矛盾 “P且﹁q”为假 “若p则q”为真 合理的推理 归缪矛盾:
(1)与已知条件矛盾;
(2)与已有公理、定理、定义矛盾;
(3)自相矛盾。间接证明(基本概念)反证法的过程包括以下三个步骤:(1) 反设——假设命题的结论不成立,即假定原命题的反面为真;(2) 归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3) 存真——由矛盾结果,断定反设不真,从而肯定原结论成立. 适宜使用反证法的情况:
(1)结论以否定形式出现;
(2)结论以“至多-------,” ,“至少------”
形式出现;
( 3)唯一性、存在性问题;
(4) 结论的反面比原结论更具体更容易
研究的命题。正难则反!间接证明(例题1)先求出周期 思路 用反证法证明 是最小正周期.间接证明(例题1)假设T是正弦函数的周期则对任意实数x都有:解:令x=0,得即从而对任意实数x都应有这与矛盾.因此,原命题成立.间接证明(例题2)已知:求证:(2)中至少有一个不小于.(1)求证: 是无理数。间接证明(例题3)间接证明(习题1)1.求证:若一个整数的平方是偶数,则这个数也是偶数.假设这个数是奇数,可以设为2k+1,证:则有而不是偶数这与原命题条件矛盾.2、用反证法证明:
如果a>b>0,那么3、已知a≠0,求证关于x的方程ax=b有且只有一个根。已知:在⊙O中,弦AB、CD相交于P,且AB、CD不全是直径;
求证:AB、CD不能互相平分。ABCD3. 设函数,求证:中至少有一个不小于1.4、求证:圆的两条不全是直径的相交弦不能互相平分.间接证明(回顾小结)间接证明 反证法 同一法 枚举法 完全归纳法
否定结论 q 导致逻辑矛盾 “P且﹁q”为假 “若p则q”为真 合理的推理 归缪矛盾:
(1)与已知条件矛盾;
(2)与已有公理、定理、定义矛盾;
(3)自相矛盾。间接证明(基本概念)反证法的过程包括以下三个步骤:(1) 反设——假设命题的结论不成立,即假定原命题的反面为真;(2) 归谬——从反设和已知条件出发,经过一系列正确的逻辑推理,得出矛盾结果;(3) 存真——由矛盾结果,断定反设不真,从而肯定原结论成立. 适宜使用反证法的情况:
(1)结论以否定形式出现;
(2)结论以“至多-------,” ,“至少------”
形式出现;
( 3)唯一性、存在性问题;
(4) 结论的反面比原结论更具体更容易
研究的命题。正难则反!间接证明(例题1)先求出周期 思路 用反证法证明 是最小正周期.间接证明(例题1)假设T是正弦函数的周期则对任意实数x都有:解:令x=0,得即从而对任意实数x都应有这与矛盾.因此,原命题成立.间接证明(例题2)已知:求证:(2)中至少有一个不小于.(1)求证: 是无理数。间接证明(例题3)间接证明(习题1)1.求证:若一个整数的平方是偶数,则这个数也是偶数.假设这个数是奇数,可以设为2k+1,证:则有而不是偶数这与原命题条件矛盾.2、用反证法证明:
如果a>b>0,那么3、已知a≠0,求证关于x的方程ax=b有且只有一个根。已知:在⊙O中,弦AB、CD相交于P,且AB、CD不全是直径;
求证:AB、CD不能互相平分。ABCD3. 设函数,求证:中至少有一个不小于1.4、求证:圆的两条不全是直径的相交弦不能互相平分.间接证明(回顾小结)间接证明 反证法 同一法 枚举法 完全归纳法
