鲁教版九年级数学上册第二单元直角三角形的边角关系2.5三角函数的应用学案(第2课时)
文档属性
| 名称 | 鲁教版九年级数学上册第二单元直角三角形的边角关系2.5三角函数的应用学案(第2课时) |
|
|
| 格式 | zip | ||
| 文件大小 | 230.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-08-04 22:21:37 | ||
图片预览


文档简介
鲁教版九年级数学上册第二单元直角三角形的边角关系2.5三角函数的应用(第2课时)
学习目标:
1、了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
2、逐步培养分析问题、解决问题的能力.
学习重难点:
1、将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
2、学习实际问题转化成数学模型。
学习过程
一、预习提纲
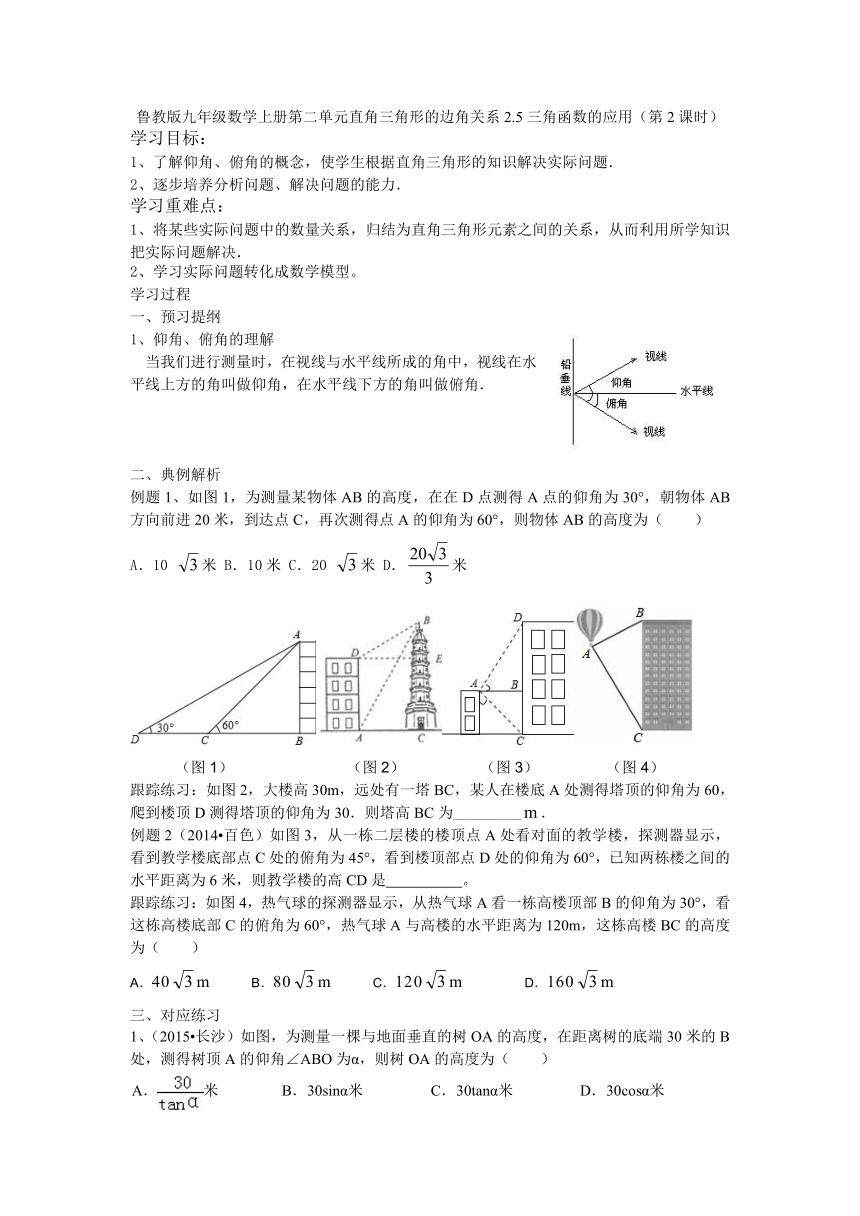
1、仰角、俯角的理解
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
二、典例解析
例题1、如图1,为测量某物体AB的高度,在在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10 米 B.10米 C.20 米 D.米
(图1) (图2) (图3) (图4)
跟踪练习:如图2,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60,爬到楼顶D测得塔顶的仰角为30.则塔高BC为_________.
例题2(2014 百色)如图3,从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是 。
跟踪练习:如图4,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
A.40m B.80m C.120m D.160m
三、对应练习
1、(2015 长沙)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B. 30sinα米 C. 30tanα米 D. 30cosα米
(1题图) (2题图) (3题图)
2、(2015 衡阳)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B. 51 C. 50+1 D. 101
3、(2015 河北模拟)2014年12月28日,亚航QZ8501客机失联,客机上共载有162人.媒体称2014年堪称航空史上的黑暗年,至少有6架次客机发生事故.某直升飞机在某次太平洋上参加救援时,飞机在距离海平面150米的上空点M处,发现A,B两块客机残骸(N,A,B在同一条直线上),此时从点M处测得A的俯角为30°,B的俯角为60°,如图所示,则A,B两块飞机残骸的距离为( )
A.150米 B. 100米 C.(150﹣75)米 D. 50米
4、(2015 潍坊模拟)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是 m.
(4题图) (5题图) (6题图) (7题图)
5、(2015 安徽)如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(=1.7).
四、中考演练
6、(2015 门头沟区)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度 m.
7、(2015 潜江)热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
8、(2015 潍坊)观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
9、(2015 宁波)如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是 m(结果保留根号)
10、(2015 德州)如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度均为 m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
11、(2015 新乡二模)图①中的铁塔位于我省开封市的铁塔公园,素有“天下第一塔”之称.为了测得铁塔EF的高度,小明利用自制的测角仪AC在C点测得塔顶E的仰角为45°,从点A向正前方行进23米到B赴,再用测角仪在D点测得塔顶E的仰角为60°.已知测角仪AC和BD的高度均为1.5米,AB所在的水平线AB⊥EF于点F(如图②),求铁塔EF的高度(结果精确到0.1米,≈1.73).
鲁教版九年级数学上册第二单元直角三角形的边角关系2.5三角函数的应用(第2课时)
参考答案
C.2、C.3、B.4、10.
5、解:如图,过点B作BE⊥CD于点E,根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,∴四边形ABEC为矩形.∴CE=AB=12m.
在Rt△CBE中,cot∠CBE=,∴BE=CE cot30°=12×=12.
在Rt△BDE中,由∠DBE=45°,得DE=BE=12.
∴CD=CE+DE=12(+1)≈32.4.
答:楼房CD的高度约为32.4m.
(5题图) (7题图)
6、解:设DB=xm,在Rt△ADB中,AB=xtan60°=xm,
在Rt△ACB中,=tan30°,整理得,=,解得,3x=x+10,x=5,
则AB=5m.故答案为5.
7、解:过A作AE⊥BC,交CB的延长线于点E,在Rt△ACD中,
∵∠CAD=30°,AD=420米,∴CD=AD tan30°=420×=140(米),∴AE=CD=140米.
在Rt△ABE中,∵∠BAE=30°,AE=140米,∴BE=AE tan30°=140×=140(米),
∴BC=AD﹣BE=420﹣140=280(米),答:这栋楼的高度为280米.
8、解:∵爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,∴∠ADB=30°,
在Rt△ABD中,tan30°=,解得,=,∴AD=45,
∵在一楼房的底端A点处观测观光塔顶端C处的仰角是60°,∴在Rt△ACD中,
CD=AD tan60°=45×=135米.故答案为135米.
9、 解:在Rt△ACD中,∵tan∠ACD=,∴tan30°=,∴=,∴AD=3m,
在Rt△BCD中,∵∠BCD=45°,∴BD=CD=9m,
∴AB=AD+BD=3+9(m).故答案为:3+9.
10、解:根据题意得:EF⊥AC,CD∥FE,∴四边形CDEF是矩形,
已知底部B的仰角为45°即∠BEF=45°,∴∠EBF=45°,∴CD=EF=FB=38,
在Rt△AEF中,AF=EF tan50°=38×1.19≈45.22∴AB=AF﹣BF=45.22﹣38≈7.2,
∴旗杆的高约为7米.
故答案为:7.2.
11、解:设EG=x米,则CG=x米,DG=(x﹣23)米,
在Rt△EDG中,=tan60°,∴=,解得x≈54.395,
EF≈54.395+1.5≈55.9米.
答:铁塔EF高为55.9米.
学习目标:
1、了解仰角、俯角的概念,使学生根据直角三角形的知识解决实际问题.
2、逐步培养分析问题、解决问题的能力.
学习重难点:
1、将某些实际问题中的数量关系,归结为直角三角形元素之间的关系,从而利用所学知识把实际问题解决.
2、学习实际问题转化成数学模型。
学习过程
一、预习提纲
1、仰角、俯角的理解
当我们进行测量时,在视线与水平线所成的角中,视线在水平线上方的角叫做仰角,在水平线下方的角叫做俯角.
二、典例解析
例题1、如图1,为测量某物体AB的高度,在在D点测得A点的仰角为30°,朝物体AB方向前进20米,到达点C,再次测得点A的仰角为60°,则物体AB的高度为( )
A.10 米 B.10米 C.20 米 D.米
(图1) (图2) (图3) (图4)
跟踪练习:如图2,大楼高30m,远处有一塔BC,某人在楼底A处测得塔顶的仰角为60,爬到楼顶D测得塔顶的仰角为30.则塔高BC为_________.
例题2(2014 百色)如图3,从一栋二层楼的楼顶点A处看对面的教学楼,探测器显示,看到教学楼底部点C处的俯角为45°,看到楼顶部点D处的仰角为60°,已知两栋楼之间的水平距离为6米,则教学楼的高CD是 。
跟踪练习:如图4,热气球的探测器显示,从热气球A看一栋高楼顶部B的仰角为30°,看这栋高楼底部C的俯角为60°,热气球A与高楼的水平距离为120m,这栋高楼BC的高度为( )
A.40m B.80m C.120m D.160m
三、对应练习
1、(2015 长沙)如图,为测量一棵与地面垂直的树OA的高度,在距离树的底端30米的B处,测得树顶A的仰角∠ABO为α,则树OA的高度为( )
A.米 B. 30sinα米 C. 30tanα米 D. 30cosα米
(1题图) (2题图) (3题图)
2、(2015 衡阳)如图,为了测得电视塔的高度AB,在D处用高为1米的测角仪CD,测得电视塔顶端A的仰角为30°,再向电视塔方向前进100米达到F处,又测得电视塔顶端A的仰角为60°,则这个电视塔的高度AB(单位:米)为( )
A.50 B. 51 C. 50+1 D. 101
3、(2015 河北模拟)2014年12月28日,亚航QZ8501客机失联,客机上共载有162人.媒体称2014年堪称航空史上的黑暗年,至少有6架次客机发生事故.某直升飞机在某次太平洋上参加救援时,飞机在距离海平面150米的上空点M处,发现A,B两块客机残骸(N,A,B在同一条直线上),此时从点M处测得A的俯角为30°,B的俯角为60°,如图所示,则A,B两块飞机残骸的距离为( )
A.150米 B. 100米 C.(150﹣75)米 D. 50米
4、(2015 潍坊模拟)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进20m到达点D处,又测得点 A的仰角为60°,则建筑物AB的高度是 m.
(4题图) (5题图) (6题图) (7题图)
5、(2015 安徽)如图,平台AB高为12m,在B处测得楼房CD顶部点D的仰角为45°,底部点C的俯角为30°,求楼房CD的高度(=1.7).
四、中考演练
6、(2015 门头沟区)某中学初三年级的学生开展测量物体高度的实践活动,他们要测量一幢建筑物AB的高度.如图,他们先在点C处测得建筑物AB的顶点A的仰角为30°,然后向建筑物AB前进10m到达点D处,又测得点A的仰角为60°,那么建筑物AB的高度 m.
7、(2015 潜江)热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处于地面距离为420米,求这栋楼的高度.
8、(2015 潍坊)观光塔是潍坊市区的标志性建筑,为测量其高度,如图,一人先在附近一楼房的底端A点处观测观光塔顶端C处的仰角是60°,然后爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°.已知楼房高AB约是45m,根据以上观测数据可求观光塔的高CD是 m.
9、(2015 宁波)如图,在数学活动课中,小敏为了测量校园内旗杆AB的高度.站在教学楼的C处测得旗杆底端B的俯角为45°,测得旗杆顶端A的仰角为30°.若旗杆与教学楼的距离为9m,则旗杆AB的高度是 m(结果保留根号)
10、(2015 德州)如图,某建筑物BC上有一旗杆AB,从与BC相距38m的D处观测旗杆顶部A的仰角为50°,观测旗杆底部B的仰角为45°,则旗杆的高度均为 m.(结果精确到0.1m,参考数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
11、(2015 新乡二模)图①中的铁塔位于我省开封市的铁塔公园,素有“天下第一塔”之称.为了测得铁塔EF的高度,小明利用自制的测角仪AC在C点测得塔顶E的仰角为45°,从点A向正前方行进23米到B赴,再用测角仪在D点测得塔顶E的仰角为60°.已知测角仪AC和BD的高度均为1.5米,AB所在的水平线AB⊥EF于点F(如图②),求铁塔EF的高度(结果精确到0.1米,≈1.73).
鲁教版九年级数学上册第二单元直角三角形的边角关系2.5三角函数的应用(第2课时)
参考答案
C.2、C.3、B.4、10.
5、解:如图,过点B作BE⊥CD于点E,根据题意,∠DBE=45°,∠CBE=30°.
∵AB⊥AC,CD⊥AC,∴四边形ABEC为矩形.∴CE=AB=12m.
在Rt△CBE中,cot∠CBE=,∴BE=CE cot30°=12×=12.
在Rt△BDE中,由∠DBE=45°,得DE=BE=12.
∴CD=CE+DE=12(+1)≈32.4.
答:楼房CD的高度约为32.4m.
(5题图) (7题图)
6、解:设DB=xm,在Rt△ADB中,AB=xtan60°=xm,
在Rt△ACB中,=tan30°,整理得,=,解得,3x=x+10,x=5,
则AB=5m.故答案为5.
7、解:过A作AE⊥BC,交CB的延长线于点E,在Rt△ACD中,
∵∠CAD=30°,AD=420米,∴CD=AD tan30°=420×=140(米),∴AE=CD=140米.
在Rt△ABE中,∵∠BAE=30°,AE=140米,∴BE=AE tan30°=140×=140(米),
∴BC=AD﹣BE=420﹣140=280(米),答:这栋楼的高度为280米.
8、解:∵爬到该楼房顶端B点处观测观光塔底部D处的俯角是30°,∴∠ADB=30°,
在Rt△ABD中,tan30°=,解得,=,∴AD=45,
∵在一楼房的底端A点处观测观光塔顶端C处的仰角是60°,∴在Rt△ACD中,
CD=AD tan60°=45×=135米.故答案为135米.
9、 解:在Rt△ACD中,∵tan∠ACD=,∴tan30°=,∴=,∴AD=3m,
在Rt△BCD中,∵∠BCD=45°,∴BD=CD=9m,
∴AB=AD+BD=3+9(m).故答案为:3+9.
10、解:根据题意得:EF⊥AC,CD∥FE,∴四边形CDEF是矩形,
已知底部B的仰角为45°即∠BEF=45°,∴∠EBF=45°,∴CD=EF=FB=38,
在Rt△AEF中,AF=EF tan50°=38×1.19≈45.22∴AB=AF﹣BF=45.22﹣38≈7.2,
∴旗杆的高约为7米.
故答案为:7.2.
11、解:设EG=x米,则CG=x米,DG=(x﹣23)米,
在Rt△EDG中,=tan60°,∴=,解得x≈54.395,
EF≈54.395+1.5≈55.9米.
答:铁塔EF高为55.9米.
