6.2.2 解一元一次方程 第1课时 课件 2023-2024学年初中数学华东师大版七年级下册(共17张PPT)
文档属性
| 名称 | 6.2.2 解一元一次方程 第1课时 课件 2023-2024学年初中数学华东师大版七年级下册(共17张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 216.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-20 22:26:17 | ||
图片预览





文档简介
(共17张PPT)
第六章 一元一次方程
6.2.2 解一元一次方程
第1课时
学习导航
学习目标
典型例题
课堂总结
概念剖析
当堂检测
新课导入
一、学习目标
1.了解一元一次方程的概念,能判断一个方程是不是一元一次方程;(重点)
2.熟练掌握解含有括号的一元一次方程;(难点)
二、新课导入
生活中,我们在吃鸡蛋等带壳的食物的时候,要先去壳;而在我们的数学中,解形如 6x – 3(x+2) = 3 这样带“壳”的方程的时候也要先去掉这层壳,方便我们“大快朵颐”,怎么来去“壳”呢?
6x – 3(x+2) = 3
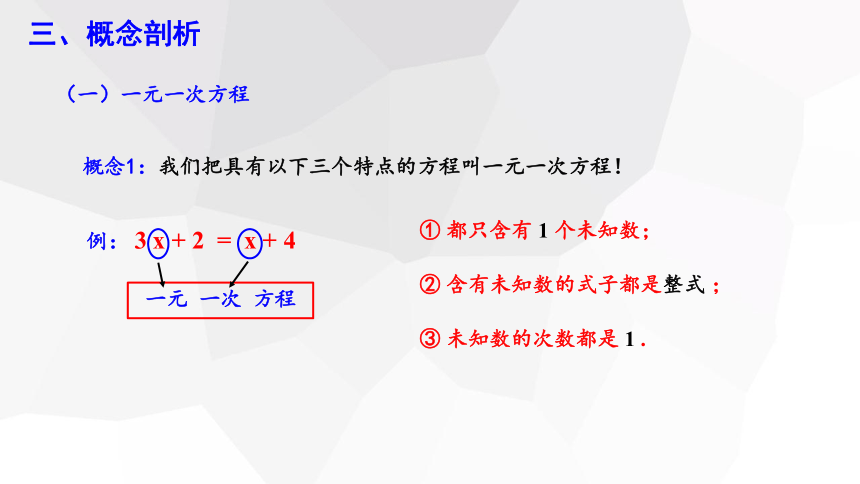
例: 3 x + 2 = x + 4
一元 一次 方程
① 都只含有 1 个未知数;
② 含有未知数的式子都是整式 ;
③ 未知数的次数都是 1 .
三、概念剖析
(一)一元一次方程
概念1:我们把具有以下三个特点的方程叫一元一次方程!
概念2:方程、方程的解、一元一次方程
方程:含有未知数的等式叫做方程;
方程的解:能使方程两边相等的未知数的值,叫做方程的解;
一元一次方程:只含有1个未知数,并且含有未知数的式子都是整式,未知数的次数都是1的方程叫做一元一次方程.
三、概念剖析
概念3:含括号的一元一次方程的解法
① 方程中含有括号时,一般先去括号; ② 再移项、合并同类项;
③ 将未知数的系数化为1.
三、概念剖析
(二)含括号的一元一次方程的解法
例:解方程:2(x+1) = 10 – (x – 1);
分析:先去括号,再移项、合并同类项,最后将未知数系数化为1即可;
解:方程 2(x+1) = 10 – (x – 1) :
去括号得 2x + 2 = 10 – x + 1;
移项得 2x+x= 10 + 1 – 2 ;
合并同类项得 3x = 9; 解得x = 3 .
例1:已知 2x3m+4 + 4= 0 是关于x的一元一次方程,求m和x的值?
分析:根据一元一次方程的概念可知:
(1)未知数的次数为1,即:3m + 4 = 1,得 m = -1;
(2)方程2x + 4 = 0:移项得 2x = -4;系数化为1得 x = -2;
解:2x3m+4 + 4 = 0 是关于x的一元一次方程,解得 m = -1,x = -2.
(一)一元一次方程及其解
四、典型例题
总结:依据一元一次方程的概念,找出隐含的等量关系,如 3m + 4 = 1.
1. 已知 是关于x的一元一次方程,求m的值并判断x=2是否为该方程的解.
分析:找出题中一元一次方程隐含的等量关系: 即可解答;
解:由上述等量关系,解得 m = 1;
将m = 1代入方程得:2x = 4;
再由题意将 x = 2 代入方程 2x = 4 ,解得方程左边 = 右边;
故x = 2是方程的解.
【当堂检测】
2. 下列方程中,是一元一次方程的是 ( )
A. x–1= y B. x2–1 = 0 C. 2x–y = 3 D. x–3 = 2
分析:A选项有两个未知数,不属于一元一次方程;B选项是二次方程;C选项有两个未知数;D选项为一元一次方程 . 故选D.
D
【当堂检测】
例2:请去除下列式子的括号:
(1)a2 – ( 3a – 2b + 4c ) ;(2)4a2 + ( – 3a + 2b ) ;(3)2x2 – 3( x – 1 ) ;
四、典型例题
(二)解含有括号的一元一次方程
分析:按去括号法则解答即可;
解:(1)a2 – ( 3a – 2b + 4c ) = a2 – 3a + 2b – 4c ;
(2)4a2 + ( – 3a + 2b ) = 4a2 – 3a + 2b ;
(3)2x2 – 3( x – 1 ) = 2x2 – 3x + 3 .
总结:去括号注意事项:
① 如果括号前面是“ + ”号,括号里各项不变号;
② 如果括号前面是“ – ”号,括号里各项都改变符号;
③ 在去括号时,括号前面的因数要与括号里面的每一项都要相乘.
四、典型例题
例3:解下列方程:
(1)3(2–x) = 2(3+x); (2)2(1–3y) – 5(y+2) = 3;
四、典型例题
解:(1) 3 (2–x) = 2 (3+x):
去括号得 6–3x = 6+2x ;
移项得 –2x–3x = 0;
合并同类项得–5x = 0;
解得 x = 0 ;
(2) 2(1–3y) – 5(y+2) = 3:
去括号得 2 – 6y – 5y – 10 = 3 ;
移项得 – 6y – 5y = 3 – 2 + 10 ;
合并同类项得 – 11y = 11;
解得 x = – 1 ;
分析:先去括号,再移项、合并同类项,最后将未知数系数化为1即可;
四、典型例题
去括号解一元一次方程的一般步骤及注意事项:
步骤 注意事项
去括号 注意符号,防止漏乘;
移项 移项要变号,防止漏项;
合并同类项 系数为1或-1时,记得省略1;
系数化为1 方程两边都除以系数.
3. 将方程3( x – 1 ) – 2( x – 3 ) = 5( 1 – x )去括号得 ( )
A. 3x – 1 – 2x – 3 = 5 – x B. 3x – 1 – 2x + 3 = 5 – x
C. 3x – 3 – 2x – 6 = 5 – 5x D. 3x – 3 – 2x + 6 = 5 – 5x
D
分析:去括号得:3x – 3 – ( 2x – 6 ) = 5 – 5x,则3x – 3 – 2x + 6 = 5 – 5x.
【当堂检测】
【当堂检测】
4. 解下列方程:
(1)6x=-2(3x-5)+10; (2)-2(x+5)=3(x-5)-6
解:(1)去括号,得:
6x=-6x+10+10
移项,得:6x+6x=10+10
合并同类项,得:12x=20
(2)去括号,得:
-2x-10=3x-15-6
移项,得:-2x-3x=-15-6+10
合并同类项,得:-5x=-11
系数化为1,得:
系数化为1,得:
五、课堂总结
第六章 一元一次方程
6.2.2 解一元一次方程
第1课时
学习导航
学习目标
典型例题
课堂总结
概念剖析
当堂检测
新课导入
一、学习目标
1.了解一元一次方程的概念,能判断一个方程是不是一元一次方程;(重点)
2.熟练掌握解含有括号的一元一次方程;(难点)
二、新课导入
生活中,我们在吃鸡蛋等带壳的食物的时候,要先去壳;而在我们的数学中,解形如 6x – 3(x+2) = 3 这样带“壳”的方程的时候也要先去掉这层壳,方便我们“大快朵颐”,怎么来去“壳”呢?
6x – 3(x+2) = 3
例: 3 x + 2 = x + 4
一元 一次 方程
① 都只含有 1 个未知数;
② 含有未知数的式子都是整式 ;
③ 未知数的次数都是 1 .
三、概念剖析
(一)一元一次方程
概念1:我们把具有以下三个特点的方程叫一元一次方程!
概念2:方程、方程的解、一元一次方程
方程:含有未知数的等式叫做方程;
方程的解:能使方程两边相等的未知数的值,叫做方程的解;
一元一次方程:只含有1个未知数,并且含有未知数的式子都是整式,未知数的次数都是1的方程叫做一元一次方程.
三、概念剖析
概念3:含括号的一元一次方程的解法
① 方程中含有括号时,一般先去括号; ② 再移项、合并同类项;
③ 将未知数的系数化为1.
三、概念剖析
(二)含括号的一元一次方程的解法
例:解方程:2(x+1) = 10 – (x – 1);
分析:先去括号,再移项、合并同类项,最后将未知数系数化为1即可;
解:方程 2(x+1) = 10 – (x – 1) :
去括号得 2x + 2 = 10 – x + 1;
移项得 2x+x= 10 + 1 – 2 ;
合并同类项得 3x = 9; 解得x = 3 .
例1:已知 2x3m+4 + 4= 0 是关于x的一元一次方程,求m和x的值?
分析:根据一元一次方程的概念可知:
(1)未知数的次数为1,即:3m + 4 = 1,得 m = -1;
(2)方程2x + 4 = 0:移项得 2x = -4;系数化为1得 x = -2;
解:2x3m+4 + 4 = 0 是关于x的一元一次方程,解得 m = -1,x = -2.
(一)一元一次方程及其解
四、典型例题
总结:依据一元一次方程的概念,找出隐含的等量关系,如 3m + 4 = 1.
1. 已知 是关于x的一元一次方程,求m的值并判断x=2是否为该方程的解.
分析:找出题中一元一次方程隐含的等量关系: 即可解答;
解:由上述等量关系,解得 m = 1;
将m = 1代入方程得:2x = 4;
再由题意将 x = 2 代入方程 2x = 4 ,解得方程左边 = 右边;
故x = 2是方程的解.
【当堂检测】
2. 下列方程中,是一元一次方程的是 ( )
A. x–1= y B. x2–1 = 0 C. 2x–y = 3 D. x–3 = 2
分析:A选项有两个未知数,不属于一元一次方程;B选项是二次方程;C选项有两个未知数;D选项为一元一次方程 . 故选D.
D
【当堂检测】
例2:请去除下列式子的括号:
(1)a2 – ( 3a – 2b + 4c ) ;(2)4a2 + ( – 3a + 2b ) ;(3)2x2 – 3( x – 1 ) ;
四、典型例题
(二)解含有括号的一元一次方程
分析:按去括号法则解答即可;
解:(1)a2 – ( 3a – 2b + 4c ) = a2 – 3a + 2b – 4c ;
(2)4a2 + ( – 3a + 2b ) = 4a2 – 3a + 2b ;
(3)2x2 – 3( x – 1 ) = 2x2 – 3x + 3 .
总结:去括号注意事项:
① 如果括号前面是“ + ”号,括号里各项不变号;
② 如果括号前面是“ – ”号,括号里各项都改变符号;
③ 在去括号时,括号前面的因数要与括号里面的每一项都要相乘.
四、典型例题
例3:解下列方程:
(1)3(2–x) = 2(3+x); (2)2(1–3y) – 5(y+2) = 3;
四、典型例题
解:(1) 3 (2–x) = 2 (3+x):
去括号得 6–3x = 6+2x ;
移项得 –2x–3x = 0;
合并同类项得–5x = 0;
解得 x = 0 ;
(2) 2(1–3y) – 5(y+2) = 3:
去括号得 2 – 6y – 5y – 10 = 3 ;
移项得 – 6y – 5y = 3 – 2 + 10 ;
合并同类项得 – 11y = 11;
解得 x = – 1 ;
分析:先去括号,再移项、合并同类项,最后将未知数系数化为1即可;
四、典型例题
去括号解一元一次方程的一般步骤及注意事项:
步骤 注意事项
去括号 注意符号,防止漏乘;
移项 移项要变号,防止漏项;
合并同类项 系数为1或-1时,记得省略1;
系数化为1 方程两边都除以系数.
3. 将方程3( x – 1 ) – 2( x – 3 ) = 5( 1 – x )去括号得 ( )
A. 3x – 1 – 2x – 3 = 5 – x B. 3x – 1 – 2x + 3 = 5 – x
C. 3x – 3 – 2x – 6 = 5 – 5x D. 3x – 3 – 2x + 6 = 5 – 5x
D
分析:去括号得:3x – 3 – ( 2x – 6 ) = 5 – 5x,则3x – 3 – 2x + 6 = 5 – 5x.
【当堂检测】
【当堂检测】
4. 解下列方程:
(1)6x=-2(3x-5)+10; (2)-2(x+5)=3(x-5)-6
解:(1)去括号,得:
6x=-6x+10+10
移项,得:6x+6x=10+10
合并同类项,得:12x=20
(2)去括号,得:
-2x-10=3x-15-6
移项,得:-2x-3x=-15-6+10
合并同类项,得:-5x=-11
系数化为1,得:
系数化为1,得:
五、课堂总结
