9.1.1 认识三角形 课件(共26张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 9.1.1 认识三角形 课件(共26张PPT) 2023-2024学年初中数学华东师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 07:44:23 | ||
图片预览






文档简介
(共26张PPT)
第九章 多边形
9.1 三角形
9.1.1 认识三角形
一、学习目标
1.掌握三角形的有关概念,会识别等腰三角形和等边三角形;
2.能按照边长关系和角的大小对三角形进行分类;了解三角形的角平分线、中线、高的概念. (重点)
二、新课导入
生活中的三角形
山峰
金字塔
现代建筑
各类标志
你还能举出其他例子吗?
三、概念剖析
(一)三角形的概念
问题1:生活中处处都有三角形的身影,请观察下面三角形的形成过程,说一说什么叫三角形?
A
B
C
定义:不在同一条直线上的三条线段首尾相接所构成的图形叫做三角形.
三、概念剖析
问题2:三角形有什么特点?
边:线段 AB,BC,CA是三角形的三条边;
顶点:点 A,B,C是三角形的三个顶点;
内角:∠A,∠B,∠ACB叫作三角形的内角,简称三角形的角;
外角:∠ACD 叫做这个三角形的外角.
总结:一个三角形有三个顶点,三条边,三个角(内角).
A
B
C
边
内角
顶点
外角
D
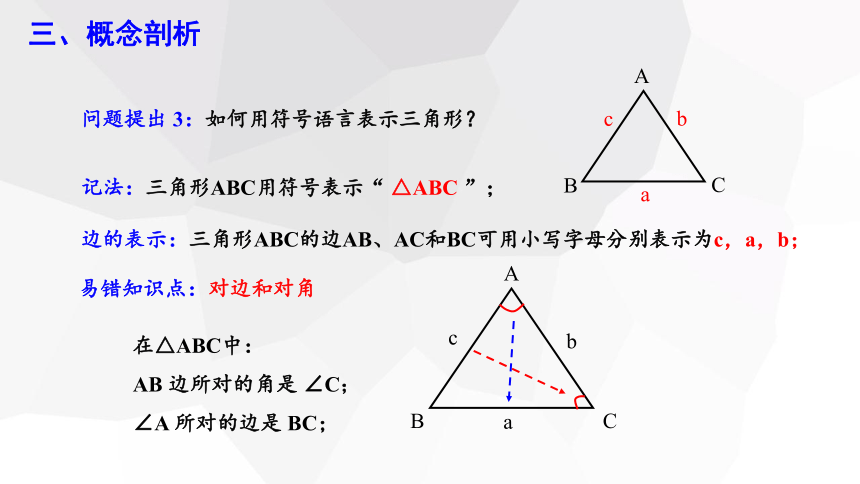
问题提出 3:如何用符号语言表示三角形?
记法:三角形ABC用符号表示“ △ABC ”;
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表示为c,a,b;
c
b
a
C
A
B
易错知识点:对边和对角
c
b
a
C
A
B
在△ABC中:
AB 边所对的角是 ∠C;
∠A 所对的边是 BC;
三、概念剖析
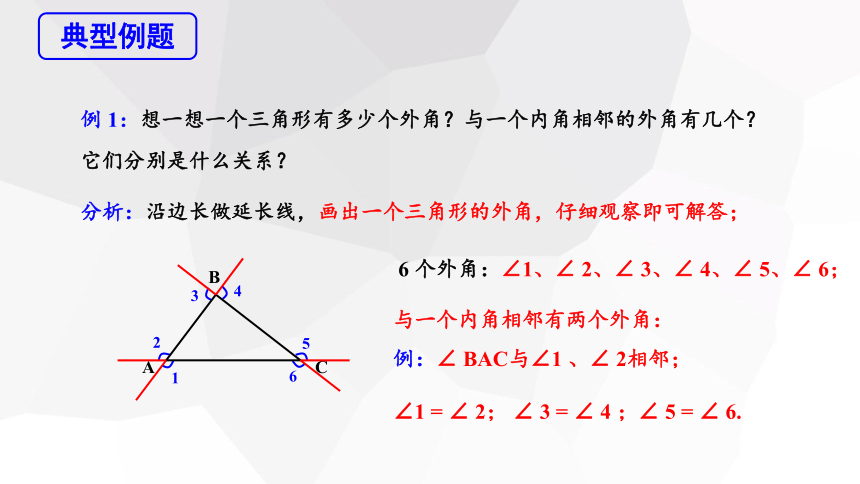
例 1:想一想一个三角形有多少个外角?与一个内角相邻的外角有几个?它们分别是什么关系?
典型例题
分析:沿边长做延长线,画出一个三角形的外角,仔细观察即可解答;
1
2
3
4
5
6
6 个外角:∠1、∠ 2、∠ 3、∠ 4、∠ 5、∠ 6;
与一个内角相邻有两个外角:
例:∠ BAC与∠1 、∠ 2相邻;
B
C
A
∠1 = ∠ 2; ∠ 3 = ∠ 4 ;∠ 5 = ∠ 6.
【当堂检测】
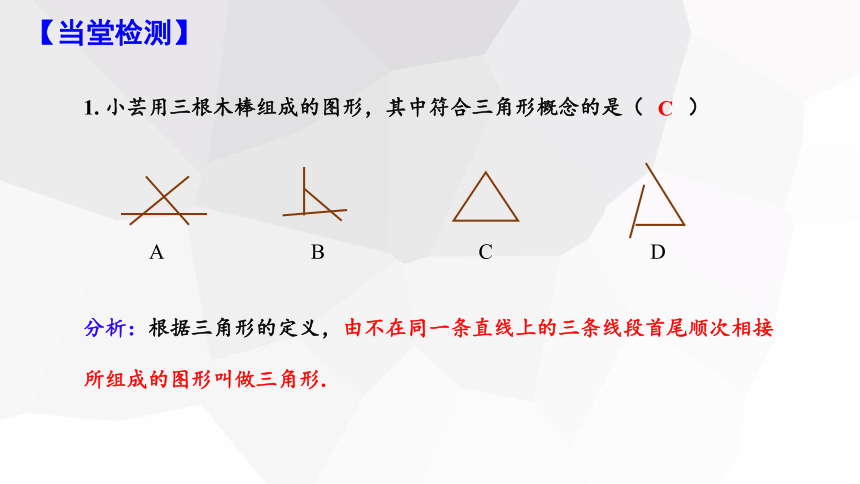
1. 小芸用三根木棒组成的图形,其中符合三角形概念的是( )
C
B
A
C
D
分析:根据三角形的定义,由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
三、概念剖析
(二)三角形的分类
在小学我们已经学习了钝角、锐角、直角.
那么在三角形中,三个角都是锐角的三角形叫做锐角三角形;
有一个角是直角的三角形叫做直角三角形;
有一个角是钝角的三角形叫做钝角三角形.
锐角三角形
钝角三角形
直角三角形
(1)按角分类:
三、概念剖析
三角形按角的大小,可分为:
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
直角三角形
锐角
三角形
钝角
三角形
也可分为:
思考:根据以上的内容,谈谈你对三角形按角分类的想法.
三、概念剖析
(2)按边分类:
三边都相等的三角形叫等边三角形(正三角形);
有两边相等的三角形叫做等腰三角形;相等的两边叫做等腰三角形的腰;
除了上面两类三角形,其余的三角形都是不等边三角形.
等边三角形
不等边三角形
等腰三角形
腰
底边
顶角
底角
三、概念剖析
按边分
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
讨论:根据上面的内容将三角形按边进行分类.
注:等边三角形是一种特殊的等腰三角形;即底边和腰相等的等腰三角形.
例 2:找一找,图中有多少个三角形,并把它们按角进行分类.
典型例题
解:图中有5个三角形,分别是:
△ABE,△DCE, △BEC,△ABC,△DCB;
锐角三角形:△ABE,△DCE;
钝角三角形:△BEC,△ABC,△DCB.
2. 下列说法正确的有 .
(1)等边三角形是特殊的等腰三角形.
(2)等腰三角形的腰和底一定不相等.
(3)等边三角形三条边相等.
【当堂检测】
(1) (3)
(三) 三角形的角平分线、中线、高
如图,在△ABC中作∠A的角平分线交BC于D点,则线段AD为△ABC的一条角平分线;这时就有:∠BAD = ∠CAD = ∠BAC.
△ABC的角平分线有三条,都是线段;
而角的平分线是射线;
总结:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做这个三角形的角平分线.
A
B
C
D
三、概念剖析
(1)三角形的角平分线:
D
三、概念剖析
试一试:任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么
发现:三角形的三条角平分线相交于一点,交点在三角形的内部.
A
B
C
F
E
三、概念剖析
(2)三角形的中线:
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线 .
A
B
C
D
一个三角形有三条中线,用同样的方法,我们还可以画出三角形的另外两条中线.
总结:在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线.
三、概念剖析
试一试:画出任意一个三角形的三条中线,我们会发现三角形的三条中线也相交于一点;我们把这个交点叫做三角形的重心.
A
B
C
D
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
F
E
三、概念剖析
我们已经知道:过直线外的一点做该直线的垂线,只能做出1条垂线.
那如果在△ABC中,我们也可以过顶点A画出对边BC的垂线,如图:
A
B
C
D
线段 AD 就是△ABC的一条高.
一个三角形有三条高,我们还可以画出三角形的另外两条高.
(3)三角形的高:
三、概念剖析
总结:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
如图,线段AD是BC边上的高.
注意:标明垂直的记号和垂足的字母.
A
B
C
D
思考:前面已经知道了三角形的角平分线和中线均会交于一点,那么三角形的高也会交于一点吗?
三、概念剖析
探究交流1:先画出一个锐角三角形,再画出这个锐角三角形的三条高;
最后观察三条高的位置关系,得出结论.
结论:
1. 锐角三角形的三条高交于同一点;
2. 锐角三角形的三条高的交点和三条高都在三角形的内部.
三、概念剖析
探究交流2:先画出一个直角三角形,再画出这个直角三角形的三条高;
最后观察三条高的位置关系,得出结论.
结论:
1. 直角三角形的三条高交于直角顶点;
2. 直角三角形的有两条高为直角边.
A
B
C
D
三、概念剖析
探究交流3:先画出一个钝角三角形,再画出这个钝角三角形的三条高;
最后观察三条高的位置关系,得出结论.
结论:
1. 钝角三角形的三条高不相交于一点;
2. 钝角三角形的三条高所在直线交于一点.
A
B
C
D
E
F
例 3:在三角形ABC中,AD为BC边上的中线,则△ABD与△ADC面积有什么关系?为什么?
典型例题
分析:根据三角形面积公式:S = ×底×高解答即可;
A
B
C
D
解:已知:AD为BC边上的中线;
所以:BD = CD;
如图,过点 A 做 BC 的垂线,即 AE ⊥ BC;
E
则:△ABD 的面积为 ×BD×AE;
△ACD 的面积为 ×CD×AE;
因为:BD = CD;
所以:△ABD 与 △ADC 面积相等;
总结:三角形的中线平分该三角形的面积.
【当堂检测】
3. 不一定在三角形内部的线段是( )
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 三角形的中位线
C
五、课堂总结
三角形
概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形;
三角形的分类
按边分:不等边三角形、 等腰三角形;
按角分:锐角三角形、直角三角形和钝角三角形;
高、中线、角平分线
三条角平分线交于三角形内部;
三条中线交于三角形内部;
三条高根据不同三角形区分;
第九章 多边形
9.1 三角形
9.1.1 认识三角形
一、学习目标
1.掌握三角形的有关概念,会识别等腰三角形和等边三角形;
2.能按照边长关系和角的大小对三角形进行分类;了解三角形的角平分线、中线、高的概念. (重点)
二、新课导入
生活中的三角形
山峰
金字塔
现代建筑
各类标志
你还能举出其他例子吗?
三、概念剖析
(一)三角形的概念
问题1:生活中处处都有三角形的身影,请观察下面三角形的形成过程,说一说什么叫三角形?
A
B
C
定义:不在同一条直线上的三条线段首尾相接所构成的图形叫做三角形.
三、概念剖析
问题2:三角形有什么特点?
边:线段 AB,BC,CA是三角形的三条边;
顶点:点 A,B,C是三角形的三个顶点;
内角:∠A,∠B,∠ACB叫作三角形的内角,简称三角形的角;
外角:∠ACD 叫做这个三角形的外角.
总结:一个三角形有三个顶点,三条边,三个角(内角).
A
B
C
边
内角
顶点
外角
D
问题提出 3:如何用符号语言表示三角形?
记法:三角形ABC用符号表示“ △ABC ”;
边的表示:三角形ABC的边AB、AC和BC可用小写字母分别表示为c,a,b;
c
b
a
C
A
B
易错知识点:对边和对角
c
b
a
C
A
B
在△ABC中:
AB 边所对的角是 ∠C;
∠A 所对的边是 BC;
三、概念剖析
例 1:想一想一个三角形有多少个外角?与一个内角相邻的外角有几个?它们分别是什么关系?
典型例题
分析:沿边长做延长线,画出一个三角形的外角,仔细观察即可解答;
1
2
3
4
5
6
6 个外角:∠1、∠ 2、∠ 3、∠ 4、∠ 5、∠ 6;
与一个内角相邻有两个外角:
例:∠ BAC与∠1 、∠ 2相邻;
B
C
A
∠1 = ∠ 2; ∠ 3 = ∠ 4 ;∠ 5 = ∠ 6.
【当堂检测】
1. 小芸用三根木棒组成的图形,其中符合三角形概念的是( )
C
B
A
C
D
分析:根据三角形的定义,由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形.
三、概念剖析
(二)三角形的分类
在小学我们已经学习了钝角、锐角、直角.
那么在三角形中,三个角都是锐角的三角形叫做锐角三角形;
有一个角是直角的三角形叫做直角三角形;
有一个角是钝角的三角形叫做钝角三角形.
锐角三角形
钝角三角形
直角三角形
(1)按角分类:
三、概念剖析
三角形按角的大小,可分为:
三角形
直角三角形
斜三角形
锐角三角形
钝角三角形
直角三角形
锐角
三角形
钝角
三角形
也可分为:
思考:根据以上的内容,谈谈你对三角形按角分类的想法.
三、概念剖析
(2)按边分类:
三边都相等的三角形叫等边三角形(正三角形);
有两边相等的三角形叫做等腰三角形;相等的两边叫做等腰三角形的腰;
除了上面两类三角形,其余的三角形都是不等边三角形.
等边三角形
不等边三角形
等腰三角形
腰
底边
顶角
底角
三、概念剖析
按边分
三边都不相等的三角形
等腰三角形
底边和腰不相等的等腰三角形
等边三角形
讨论:根据上面的内容将三角形按边进行分类.
注:等边三角形是一种特殊的等腰三角形;即底边和腰相等的等腰三角形.
例 2:找一找,图中有多少个三角形,并把它们按角进行分类.
典型例题
解:图中有5个三角形,分别是:
△ABE,△DCE, △BEC,△ABC,△DCB;
锐角三角形:△ABE,△DCE;
钝角三角形:△BEC,△ABC,△DCB.
2. 下列说法正确的有 .
(1)等边三角形是特殊的等腰三角形.
(2)等腰三角形的腰和底一定不相等.
(3)等边三角形三条边相等.
【当堂检测】
(1) (3)
(三) 三角形的角平分线、中线、高
如图,在△ABC中作∠A的角平分线交BC于D点,则线段AD为△ABC的一条角平分线;这时就有:∠BAD = ∠CAD = ∠BAC.
△ABC的角平分线有三条,都是线段;
而角的平分线是射线;
总结:在三角形中,一个内角的角平分线与它的对边相交,这个角的顶点与交点之间的线段叫做这个三角形的角平分线.
A
B
C
D
三、概念剖析
(1)三角形的角平分线:
D
三、概念剖析
试一试:任意画一个三角形,然后利用量角器画出这个三角形三个角的角平分线,你发现了什么
发现:三角形的三条角平分线相交于一点,交点在三角形的内部.
A
B
C
F
E
三、概念剖析
(2)三角形的中线:
如图,连接△ABC的顶点A和它所对的边BC的中点D,所得线段AD叫做△ABC的边BC上的中线 .
A
B
C
D
一个三角形有三条中线,用同样的方法,我们还可以画出三角形的另外两条中线.
总结:在三角形中,连接一个顶点与它对边中点的线段,叫做这个三角形这边上的中线.
三、概念剖析
试一试:画出任意一个三角形的三条中线,我们会发现三角形的三条中线也相交于一点;我们把这个交点叫做三角形的重心.
A
B
C
D
取一块质地均匀的三角形木板,顶住三条中线的交点,木板会保持平衡,这个平衡点就是这块三角形木板的重心.
F
E
三、概念剖析
我们已经知道:过直线外的一点做该直线的垂线,只能做出1条垂线.
那如果在△ABC中,我们也可以过顶点A画出对边BC的垂线,如图:
A
B
C
D
线段 AD 就是△ABC的一条高.
一个三角形有三条高,我们还可以画出三角形的另外两条高.
(3)三角形的高:
三、概念剖析
总结:从三角形的一个顶点向它的对边所在直线作垂线,顶点和垂足之间的线段叫做三角形这边上的高,简称三角形的高.
如图,线段AD是BC边上的高.
注意:标明垂直的记号和垂足的字母.
A
B
C
D
思考:前面已经知道了三角形的角平分线和中线均会交于一点,那么三角形的高也会交于一点吗?
三、概念剖析
探究交流1:先画出一个锐角三角形,再画出这个锐角三角形的三条高;
最后观察三条高的位置关系,得出结论.
结论:
1. 锐角三角形的三条高交于同一点;
2. 锐角三角形的三条高的交点和三条高都在三角形的内部.
三、概念剖析
探究交流2:先画出一个直角三角形,再画出这个直角三角形的三条高;
最后观察三条高的位置关系,得出结论.
结论:
1. 直角三角形的三条高交于直角顶点;
2. 直角三角形的有两条高为直角边.
A
B
C
D
三、概念剖析
探究交流3:先画出一个钝角三角形,再画出这个钝角三角形的三条高;
最后观察三条高的位置关系,得出结论.
结论:
1. 钝角三角形的三条高不相交于一点;
2. 钝角三角形的三条高所在直线交于一点.
A
B
C
D
E
F
例 3:在三角形ABC中,AD为BC边上的中线,则△ABD与△ADC面积有什么关系?为什么?
典型例题
分析:根据三角形面积公式:S = ×底×高解答即可;
A
B
C
D
解:已知:AD为BC边上的中线;
所以:BD = CD;
如图,过点 A 做 BC 的垂线,即 AE ⊥ BC;
E
则:△ABD 的面积为 ×BD×AE;
△ACD 的面积为 ×CD×AE;
因为:BD = CD;
所以:△ABD 与 △ADC 面积相等;
总结:三角形的中线平分该三角形的面积.
【当堂检测】
3. 不一定在三角形内部的线段是( )
A. 三角形的角平分线 B. 三角形的中线
C. 三角形的高 D. 三角形的中位线
C
五、课堂总结
三角形
概念:由不在同一条直线上的三条线段首尾顺次相接所组成的图形;
三角形的分类
按边分:不等边三角形、 等腰三角形;
按角分:锐角三角形、直角三角形和钝角三角形;
高、中线、角平分线
三条角平分线交于三角形内部;
三条中线交于三角形内部;
三条高根据不同三角形区分;
