9.1.2 三角形的内角和与外角和 第1课时 课件(共16张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 9.1.2 三角形的内角和与外角和 第1课时 课件(共16张PPT) 2023-2024学年初中数学华东师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 368.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 07:45:36 | ||
图片预览




文档简介
(共16张PPT)
第九章 多边形
9.1 三角形
9.1.2 三角形的内角和与外角和 第1课时
一、学习目标
1.能利用平行线的性质证明三角形内角和定理,并能推出直角三角形的两锐角互余;(重点)
3.能利用三角形的内角和定理解决一些简单问题;
二、新课导入
回顾:
A
B
C
内角
1. 三角形内角的定义:
在一个三角形中,相邻两边组成的角叫做三角形的内角.
2. 三角形的内角和:
我们在小学已经知道,任意一个三角形的内角和等于180°.
思考:你能通过科学的方法验证三角形的内角和等于180°吗?
三、概念剖析
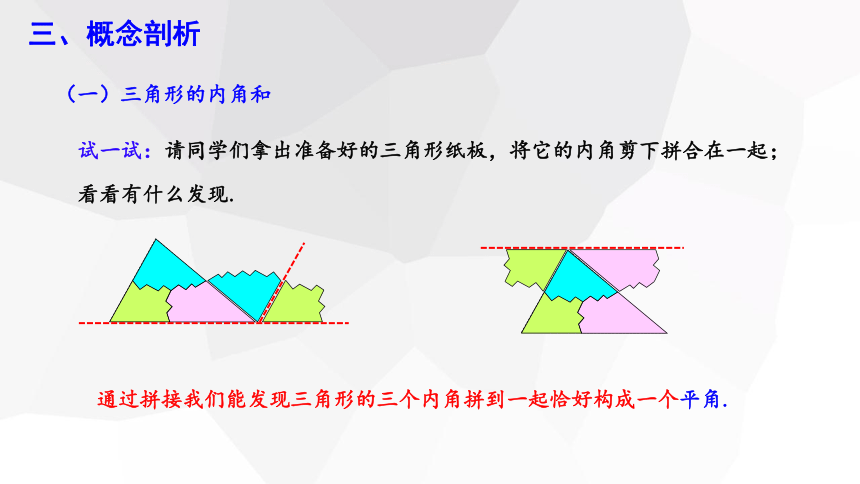
(一)三角形的内角和
试一试:请同学们拿出准备好的三角形纸板,将它的内角剪下拼合在一起;
看看有什么发现.
通过拼接我们能发现三角形的三个内角拼到一起恰好构成一个平角.
三、概念剖析
三角形有无数个,我们不可能用上述方法进行一一验证.
发现:上面拼接过程中出现了一条过三角形
顶点的直线(上图红线);
这条直线与三角形底边平行.
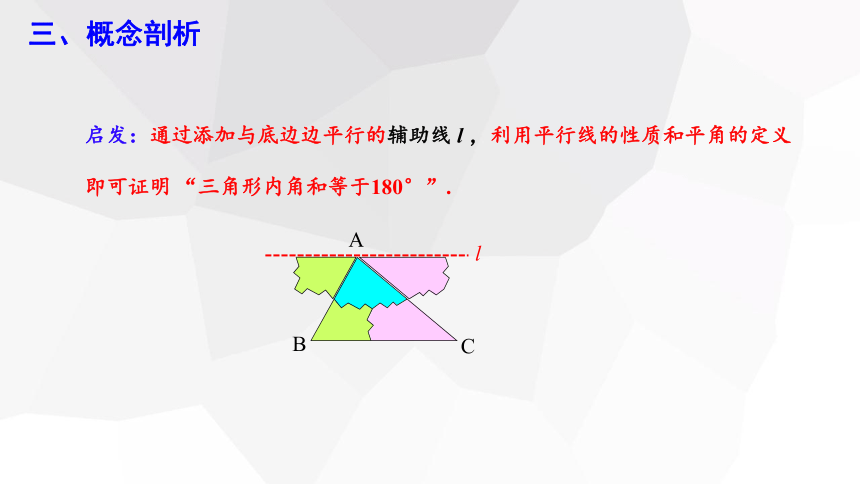
问题1:这条直线与三角形底边有什么位置关系?
思考:那有没有更加合理的方法证明呢?
三、概念剖析
启发:通过添加与底边边平行的辅助线 l ,利用平行线的性质和平角的定义即可证明 “三角形内角和等于180°”.
l
A
B
C
三、概念剖析
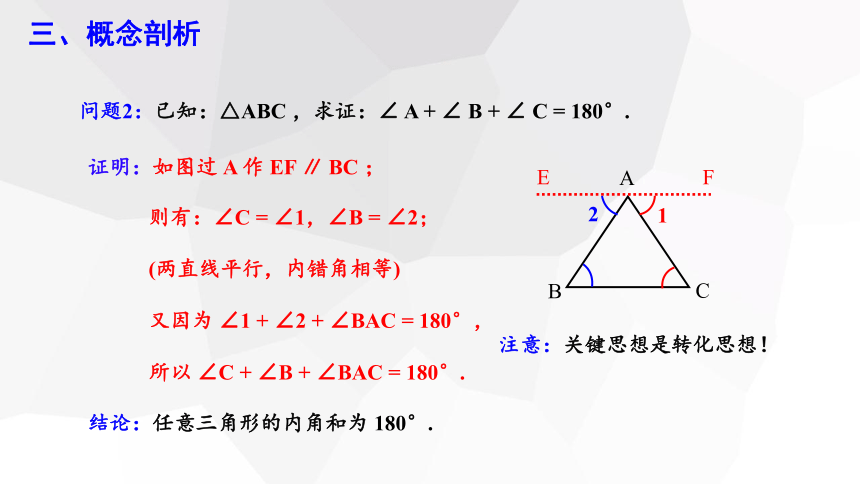
问题2:已知:△ABC ,求证:∠ A + ∠ B + ∠ C = 180°.
C
A
B
证明:如图过 A 作 EF ∥ BC ;
则有:∠C = ∠1,∠B = ∠2;
(两直线平行,内错角相等)
又因为 ∠1 + ∠2 + ∠BAC = 180°,
所以 ∠C + ∠B + ∠BAC = 180°.
F
E
1
2
结论:任意三角形的内角和为 180°.
注意:关键思想是转化思想!
三、概念剖析
归纳总结:
(1)三角形内角和定理:三角形的内角和为180°;
(2)在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线;
注:在平面几何里,辅助线通常画成虚线.
C
A
B
F
E
1
2
辅助线
例 1:一个三角形三个内角度数的比是 3:5:4 ,那么这个三角形是锐角三角形、直角三角形、钝角三角形中的哪种?
典型例题
分析:三角形内角和等于180°,已知三个内角比例关系可列方程求解.
解:依题意,设三角形的三个内角分别为:3x,5x,4x;
∴ 3x + 5x + 4x = 180°,解得 x = 15°;
∴ 这个三角形三个角分别是:45°、75°、60°;
∴ 这个三角形是锐角三角形.
【当堂检测】
1. 填空.
(1)在△ABC中,∠A = 35°,∠B = 40 °,则 △ABC 是 三角形;
(2)在△ABC中,∠A : ∠B : ∠C = 1 : 2 : 3,则 △ABC 是 三角形.
分析:根据三角形内角和定理解答即可;
钝角
直角
三、概念剖析
(二)直角三角形的性质
问题1:下图是是我们常用的直角三角尺,请计算它们的两个锐角之和.
30°+ 60°= 90°
45°+ 45°= 90°
思考:是不是所有的直角三角形的两个锐角都满足上面关系呢?
三、概念剖析
问题2:如图,在直角△ABC中, ∠C = 90°,你能求出∠A,∠B 的度数吗?为什么?你能求出 ∠A + ∠B 的度数吗
A
C
B
解:由三角形内角和定理得:∠A + ∠B + ∠C = 180°;
∵ ∠C = 90°,∴ ∠A + ∠B = 180°– 90°= 90°.
分析:题目中只给出∠C的度数,所以我们无法直接求得 ∠A、∠B 的度数.
但根据三角形内角和定理,我们可以求出∠A +∠B 的度数.
思考:通过以上两个问题,你能得出怎样的结论?
三、概念剖析
应用格式:在Rt△ABC 中,
∵ ∠C = 90°,
∴ ∠A + ∠B = 90°.
归纳总结:
(1)直角三角形的两个锐角互余;
(2)直角三角形可以用符号“ Rt △ ”表示;
如:直角三角形 ABC 可以写成 Rt△ ABC.
A
C
B
例 2:在直角三角形中,有一个锐角是另一个锐角的4倍,求这个直角三角形各个角的度数.
典型例题
分析:根据三角形的内角和定理列方程求解即可.
解:设一个锐角为 x 度,则另一个锐角为 4x 度;
那么根据三角形内角和定理:三角形内角之和为180°;
所以 x + 4x + 90°= 180°;
解得 x = 18°,则 4x = 72°;
答:三个角分别为 18°,72°,90°.
2. 如图,∠C = ∠D = 90°,AD交BC于点E.∠CAE与∠DBE有什么关系?为什么?
【当堂检测】
解:∠CAE与∠DBE相等;理由如下:
∵ 在△CAE,△DBE中:
∠C = ∠D = 90°, ∠CEA = ∠DEB;
∴ ∠CAE = 90°– ∠CEA,∠DBE = 90°– ∠DEB,
即:∠CAE = ∠DBE.
A
B
C
E
D
三角形的内角和定理
定理:三角形的内角和为 180°;
推论:直角三角形的两锐角之和为 90°.
五、课堂总结
第九章 多边形
9.1 三角形
9.1.2 三角形的内角和与外角和 第1课时
一、学习目标
1.能利用平行线的性质证明三角形内角和定理,并能推出直角三角形的两锐角互余;(重点)
3.能利用三角形的内角和定理解决一些简单问题;
二、新课导入
回顾:
A
B
C
内角
1. 三角形内角的定义:
在一个三角形中,相邻两边组成的角叫做三角形的内角.
2. 三角形的内角和:
我们在小学已经知道,任意一个三角形的内角和等于180°.
思考:你能通过科学的方法验证三角形的内角和等于180°吗?
三、概念剖析
(一)三角形的内角和
试一试:请同学们拿出准备好的三角形纸板,将它的内角剪下拼合在一起;
看看有什么发现.
通过拼接我们能发现三角形的三个内角拼到一起恰好构成一个平角.
三、概念剖析
三角形有无数个,我们不可能用上述方法进行一一验证.
发现:上面拼接过程中出现了一条过三角形
顶点的直线(上图红线);
这条直线与三角形底边平行.
问题1:这条直线与三角形底边有什么位置关系?
思考:那有没有更加合理的方法证明呢?
三、概念剖析
启发:通过添加与底边边平行的辅助线 l ,利用平行线的性质和平角的定义即可证明 “三角形内角和等于180°”.
l
A
B
C
三、概念剖析
问题2:已知:△ABC ,求证:∠ A + ∠ B + ∠ C = 180°.
C
A
B
证明:如图过 A 作 EF ∥ BC ;
则有:∠C = ∠1,∠B = ∠2;
(两直线平行,内错角相等)
又因为 ∠1 + ∠2 + ∠BAC = 180°,
所以 ∠C + ∠B + ∠BAC = 180°.
F
E
1
2
结论:任意三角形的内角和为 180°.
注意:关键思想是转化思想!
三、概念剖析
归纳总结:
(1)三角形内角和定理:三角形的内角和为180°;
(2)在这里,为了证明的需要,在原来的图形上添画的线叫做辅助线;
注:在平面几何里,辅助线通常画成虚线.
C
A
B
F
E
1
2
辅助线
例 1:一个三角形三个内角度数的比是 3:5:4 ,那么这个三角形是锐角三角形、直角三角形、钝角三角形中的哪种?
典型例题
分析:三角形内角和等于180°,已知三个内角比例关系可列方程求解.
解:依题意,设三角形的三个内角分别为:3x,5x,4x;
∴ 3x + 5x + 4x = 180°,解得 x = 15°;
∴ 这个三角形三个角分别是:45°、75°、60°;
∴ 这个三角形是锐角三角形.
【当堂检测】
1. 填空.
(1)在△ABC中,∠A = 35°,∠B = 40 °,则 △ABC 是 三角形;
(2)在△ABC中,∠A : ∠B : ∠C = 1 : 2 : 3,则 △ABC 是 三角形.
分析:根据三角形内角和定理解答即可;
钝角
直角
三、概念剖析
(二)直角三角形的性质
问题1:下图是是我们常用的直角三角尺,请计算它们的两个锐角之和.
30°+ 60°= 90°
45°+ 45°= 90°
思考:是不是所有的直角三角形的两个锐角都满足上面关系呢?
三、概念剖析
问题2:如图,在直角△ABC中, ∠C = 90°,你能求出∠A,∠B 的度数吗?为什么?你能求出 ∠A + ∠B 的度数吗
A
C
B
解:由三角形内角和定理得:∠A + ∠B + ∠C = 180°;
∵ ∠C = 90°,∴ ∠A + ∠B = 180°– 90°= 90°.
分析:题目中只给出∠C的度数,所以我们无法直接求得 ∠A、∠B 的度数.
但根据三角形内角和定理,我们可以求出∠A +∠B 的度数.
思考:通过以上两个问题,你能得出怎样的结论?
三、概念剖析
应用格式:在Rt△ABC 中,
∵ ∠C = 90°,
∴ ∠A + ∠B = 90°.
归纳总结:
(1)直角三角形的两个锐角互余;
(2)直角三角形可以用符号“ Rt △ ”表示;
如:直角三角形 ABC 可以写成 Rt△ ABC.
A
C
B
例 2:在直角三角形中,有一个锐角是另一个锐角的4倍,求这个直角三角形各个角的度数.
典型例题
分析:根据三角形的内角和定理列方程求解即可.
解:设一个锐角为 x 度,则另一个锐角为 4x 度;
那么根据三角形内角和定理:三角形内角之和为180°;
所以 x + 4x + 90°= 180°;
解得 x = 18°,则 4x = 72°;
答:三个角分别为 18°,72°,90°.
2. 如图,∠C = ∠D = 90°,AD交BC于点E.∠CAE与∠DBE有什么关系?为什么?
【当堂检测】
解:∠CAE与∠DBE相等;理由如下:
∵ 在△CAE,△DBE中:
∠C = ∠D = 90°, ∠CEA = ∠DEB;
∴ ∠CAE = 90°– ∠CEA,∠DBE = 90°– ∠DEB,
即:∠CAE = ∠DBE.
A
B
C
E
D
三角形的内角和定理
定理:三角形的内角和为 180°;
推论:直角三角形的两锐角之和为 90°.
五、课堂总结
