9.1.2 三角形的内角和与外角和 第2课时 课件(共17张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 9.1.2 三角形的内角和与外角和 第2课时 课件(共17张PPT) 2023-2024学年初中数学华东师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 222.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览


文档简介
(共17张PPT)
第九章 多边形
9.1.2 三角形的内角和与外角和 第2课时
一、学习目标
1. 知道三角形的外角和等于 360°;
2. 掌握三角形外角的两条性质,能利用三角形的外角性质解决简单问题.(重点)
二、新课导入
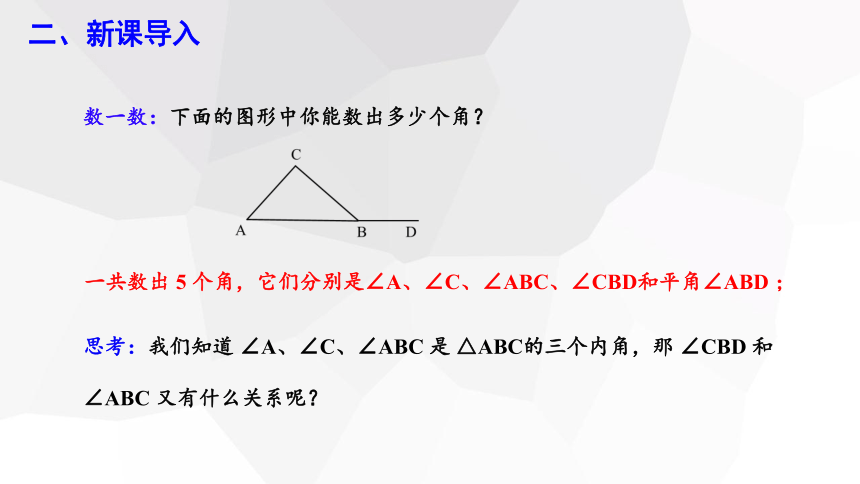
数一数:下面的图形中你能数出多少个角?
一共数出 5 个角,它们分别是∠A、∠C、∠ABC、∠CBD和平角∠ABD ;
思考:我们知道 ∠A、∠C、∠ABC 是 △ABC的三个内角,那 ∠CBD 和 ∠ABC 又有什么关系呢?
三、概念剖析
(一)三角形外角的性质
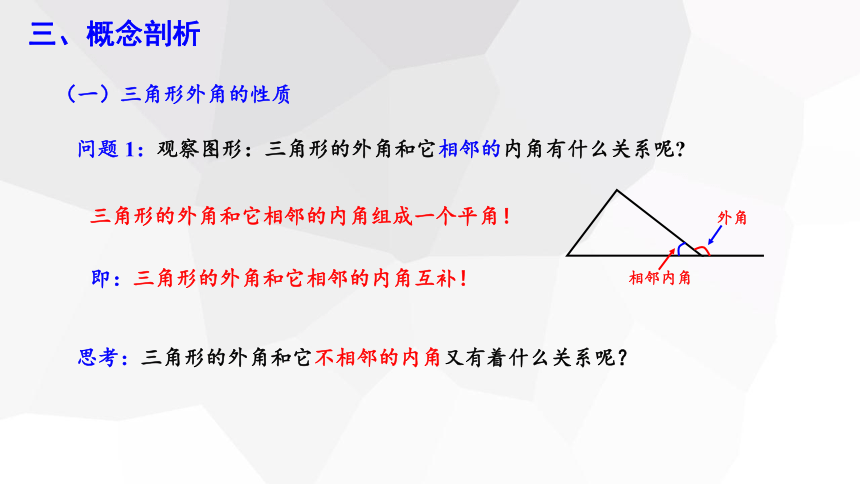
问题 1:观察图形:三角形的外角和它相邻的内角有什么关系呢
外角
相邻内角
三角形的外角和它相邻的内角组成一个平角!
即:三角形的外角和它相邻的内角互补!
思考:三角形的外角和它不相邻的内角又有着什么关系呢?
三、概念剖析
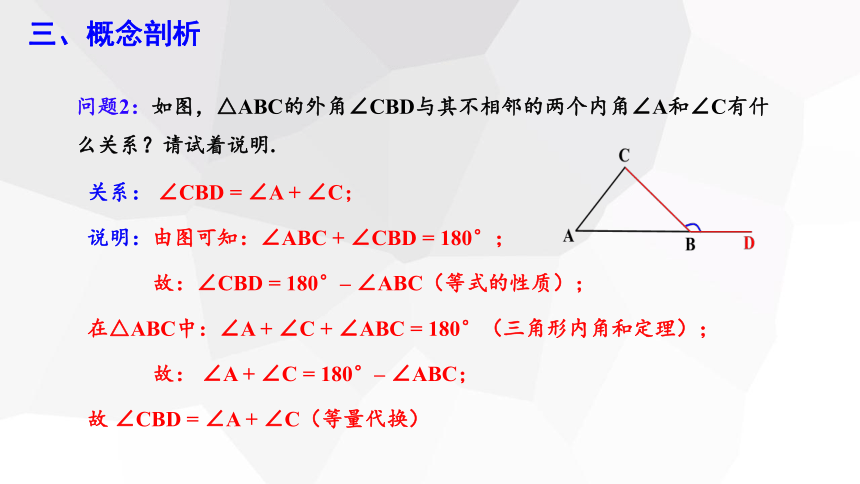
问题2:如图,△ABC的外角∠CBD与其不相邻的两个内角∠A和∠C有什么关系?请试着说明.
故:∠CBD = 180°– ∠ABC(等式的性质);
在△ABC中:∠A + ∠C + ∠ABC = 180°(三角形内角和定理);
说明:由图可知:∠ABC + ∠CBD = 180°;
故: ∠A + ∠C = 180°– ∠ABC;
故 ∠CBD = ∠A + ∠C(等量代换)
关系: ∠CBD = ∠A + ∠C;
三、概念剖析
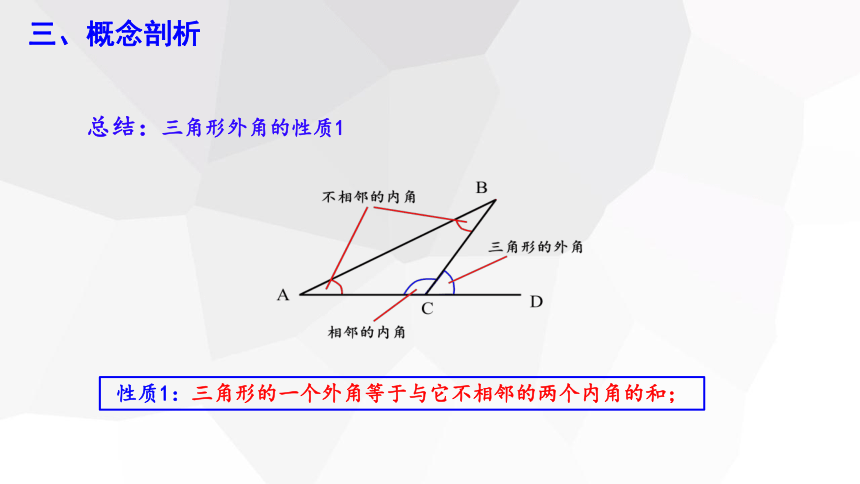
性质1:三角形的一个外角等于与它不相邻的两个内角的和;
总结:三角形外角的性质1
三、概念剖析
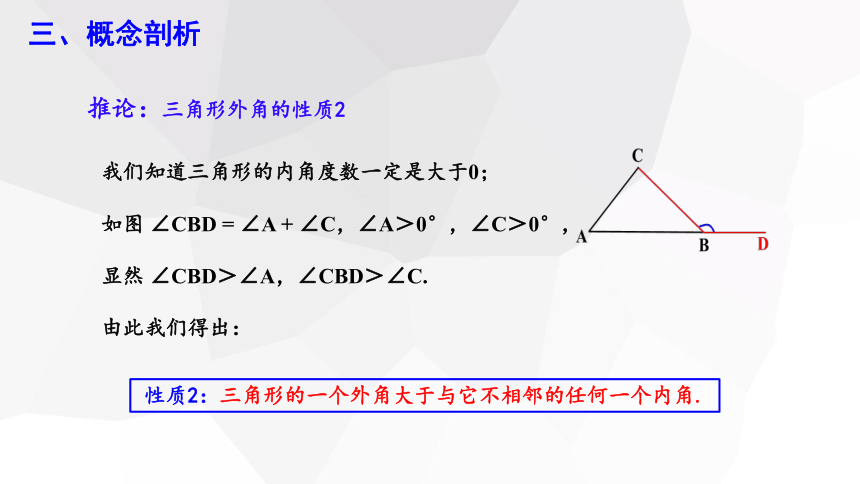
如图 ∠CBD = ∠A + ∠C,∠A>0°,∠C>0°,
我们知道三角形的内角度数一定是大于0;
显然 ∠CBD>∠A,∠CBD>∠C.
由此我们得出:
推论:三角形外角的性质2
性质2:三角形的一个外角大于与它不相邻的任何一个内角.
例 1:如图,∠A = 42°,∠ABD = 28°,∠ACE = 18°,试着求:
(1)∠BEC 的度数; (2) ∠BFC 的度数;
典型例题
分析:(1)要求 ∠BEC ,只需找出 ∠BEC 所关联的外角关系即可;
B
C
A
E
D
F
根据三角形外角的性质1可得:∠BEC = ∠A + ∠ACE;
已知:∠A = 42°,∠ACE = 18°;
代入得:∠BEC = 60°;
解:(1)如图所示,∠BEC是△AEC的一个外角;
故 ∠BEC = 60°.
(2)如图,∠A = 42°,∠ABD = 28°,∠ACE = 18°,求:∠BFC 的度数;
典型例题
分析:(2)找出 ∠BFC 所关联的外角关系即可;
B
C
A
E
D
F
根据三角形外角的性质1可得:
∠BFC = ∠EBF + ∠BEC;
由(1)可知:∠BEC = 60°;
又已知: ∠ EBF = ∠ABD = 28°;
解:(2)如图所示,∠BFC是△BEF的一个外角;
故 ∠BFC = 88°.
方法总结:
三角形组合图形问题:只给出某些角的度数,让我们求另一个角的度数;
这类题型一般解法:利用三角形内角和定理以及三角形外角的性质,找出已知角的度数和需要求的角的度数之间的关系;
分析:一般先从需要求的角与其他角的关系出发,一步步把所有未知量用已知量表示.
典型例题
【当堂检测】
1. 求出下列图形中 ∠ 1 和 ∠ 2 的度数.
70°
1
2
(2)
解:在图(1)中,∠1 = 180°– 60°– 75°= 45°,∠2 = 60°+ 75°= 135°;
在图(2)中,∠1 = 90°– 70°= 20°,∠2 = 70°+ 90°= 160°;
在图(3)中,∠2 = 50°+ 60°= 110°,∠1 = 180°– ∠2 – 40°= 30°.
1
2
60°
75°
(1)
(3)
2
1
50°
40°
60°
1
A
C
B
D
2. 如图,∠ADC = 70°, ∠1 = ∠B ,求 ∠B 的度数.
【当堂检测】
解:如图,在△ABD中: ∠ADC 是△ABD的一个外角;
即:∠ADC = ∠1 + ∠B ;
又 ∠ADC = 70°, ∠1 = ∠B;
得 ∠1 = ∠B = 35°;
故 ∠B = 35°.
三、概念剖析
(二)三角形的外角和
概念 1:从与每个内角相邻的两个外角中分别取一个相加,得到的和即是:三角形的内角和;
如图所示:∠ 1 + ∠ 2 + ∠ 3 就是△ABC的外角和;
1
2
3
B
C
A
思考:三角形的外角和为多少?
易错:① 取内角相邻的外角;
② 两个相邻外角只取一个;
问题 1:求三角形的外角和 ∠ 1 + ∠ 2 + ∠ 3 =
由图可知:∠1 + ∠BAC = 180°;
∠2 + ∠ABC = 180°;
∠3 + ∠BCA = 180°;
则:∠1 + ∠BAC + ∠2 + ∠ABC + ∠3 + ∠BCA = 3×180°;
又:∠BAC + ∠ABC + ∠BCA = 180°;
故:∠1 + ∠2 + ∠3 = 360°;
结论:三角形的外角和为360°.
1
2
3
B
C
A
三、概念剖析
解: ∵∠1、∠2、∠3 分别是△ABN、△CDP、△EFM的外角;
∴ ∠1 = ∠A + ∠B,∠2 = ∠C + ∠D,∠3 = ∠E + ∠F;
∴ ∠ A +∠ B +∠ C +∠ D +∠ E +∠ F = ∠ 1 + ∠ 2 + ∠ 3 ;
又 ∠ 1 + ∠ 2 + ∠ 3 是 △PMN 的外角和;
∴ ∠ A +∠ B +∠ C +∠ D +∠ E +∠ F = ∠ 1 + ∠ 2 + ∠ 3 = 360°
例 2:如图,试求出 ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = ________.
360°
典型例题
3. 如图,已知三角形的两个外角 ∠1 = 125°、 ∠2 = 100°,则 ∠3 的度数为( )
A. 115° B. 125°
C. 135° D. 360°
【当堂检测】
C
1
2
3
B
C
A
四、课堂总结
三角形的外角
性质 1:
三角形的一个外角等于与它不相邻的两个内角的和;
外角和:三角形的外角和为 360°;
性质 2:
三角形的一个外角大于任何一个与它不相邻的内角;
第九章 多边形
9.1.2 三角形的内角和与外角和 第2课时
一、学习目标
1. 知道三角形的外角和等于 360°;
2. 掌握三角形外角的两条性质,能利用三角形的外角性质解决简单问题.(重点)
二、新课导入
数一数:下面的图形中你能数出多少个角?
一共数出 5 个角,它们分别是∠A、∠C、∠ABC、∠CBD和平角∠ABD ;
思考:我们知道 ∠A、∠C、∠ABC 是 △ABC的三个内角,那 ∠CBD 和 ∠ABC 又有什么关系呢?
三、概念剖析
(一)三角形外角的性质
问题 1:观察图形:三角形的外角和它相邻的内角有什么关系呢
外角
相邻内角
三角形的外角和它相邻的内角组成一个平角!
即:三角形的外角和它相邻的内角互补!
思考:三角形的外角和它不相邻的内角又有着什么关系呢?
三、概念剖析
问题2:如图,△ABC的外角∠CBD与其不相邻的两个内角∠A和∠C有什么关系?请试着说明.
故:∠CBD = 180°– ∠ABC(等式的性质);
在△ABC中:∠A + ∠C + ∠ABC = 180°(三角形内角和定理);
说明:由图可知:∠ABC + ∠CBD = 180°;
故: ∠A + ∠C = 180°– ∠ABC;
故 ∠CBD = ∠A + ∠C(等量代换)
关系: ∠CBD = ∠A + ∠C;
三、概念剖析
性质1:三角形的一个外角等于与它不相邻的两个内角的和;
总结:三角形外角的性质1
三、概念剖析
如图 ∠CBD = ∠A + ∠C,∠A>0°,∠C>0°,
我们知道三角形的内角度数一定是大于0;
显然 ∠CBD>∠A,∠CBD>∠C.
由此我们得出:
推论:三角形外角的性质2
性质2:三角形的一个外角大于与它不相邻的任何一个内角.
例 1:如图,∠A = 42°,∠ABD = 28°,∠ACE = 18°,试着求:
(1)∠BEC 的度数; (2) ∠BFC 的度数;
典型例题
分析:(1)要求 ∠BEC ,只需找出 ∠BEC 所关联的外角关系即可;
B
C
A
E
D
F
根据三角形外角的性质1可得:∠BEC = ∠A + ∠ACE;
已知:∠A = 42°,∠ACE = 18°;
代入得:∠BEC = 60°;
解:(1)如图所示,∠BEC是△AEC的一个外角;
故 ∠BEC = 60°.
(2)如图,∠A = 42°,∠ABD = 28°,∠ACE = 18°,求:∠BFC 的度数;
典型例题
分析:(2)找出 ∠BFC 所关联的外角关系即可;
B
C
A
E
D
F
根据三角形外角的性质1可得:
∠BFC = ∠EBF + ∠BEC;
由(1)可知:∠BEC = 60°;
又已知: ∠ EBF = ∠ABD = 28°;
解:(2)如图所示,∠BFC是△BEF的一个外角;
故 ∠BFC = 88°.
方法总结:
三角形组合图形问题:只给出某些角的度数,让我们求另一个角的度数;
这类题型一般解法:利用三角形内角和定理以及三角形外角的性质,找出已知角的度数和需要求的角的度数之间的关系;
分析:一般先从需要求的角与其他角的关系出发,一步步把所有未知量用已知量表示.
典型例题
【当堂检测】
1. 求出下列图形中 ∠ 1 和 ∠ 2 的度数.
70°
1
2
(2)
解:在图(1)中,∠1 = 180°– 60°– 75°= 45°,∠2 = 60°+ 75°= 135°;
在图(2)中,∠1 = 90°– 70°= 20°,∠2 = 70°+ 90°= 160°;
在图(3)中,∠2 = 50°+ 60°= 110°,∠1 = 180°– ∠2 – 40°= 30°.
1
2
60°
75°
(1)
(3)
2
1
50°
40°
60°
1
A
C
B
D
2. 如图,∠ADC = 70°, ∠1 = ∠B ,求 ∠B 的度数.
【当堂检测】
解:如图,在△ABD中: ∠ADC 是△ABD的一个外角;
即:∠ADC = ∠1 + ∠B ;
又 ∠ADC = 70°, ∠1 = ∠B;
得 ∠1 = ∠B = 35°;
故 ∠B = 35°.
三、概念剖析
(二)三角形的外角和
概念 1:从与每个内角相邻的两个外角中分别取一个相加,得到的和即是:三角形的内角和;
如图所示:∠ 1 + ∠ 2 + ∠ 3 就是△ABC的外角和;
1
2
3
B
C
A
思考:三角形的外角和为多少?
易错:① 取内角相邻的外角;
② 两个相邻外角只取一个;
问题 1:求三角形的外角和 ∠ 1 + ∠ 2 + ∠ 3 =
由图可知:∠1 + ∠BAC = 180°;
∠2 + ∠ABC = 180°;
∠3 + ∠BCA = 180°;
则:∠1 + ∠BAC + ∠2 + ∠ABC + ∠3 + ∠BCA = 3×180°;
又:∠BAC + ∠ABC + ∠BCA = 180°;
故:∠1 + ∠2 + ∠3 = 360°;
结论:三角形的外角和为360°.
1
2
3
B
C
A
三、概念剖析
解: ∵∠1、∠2、∠3 分别是△ABN、△CDP、△EFM的外角;
∴ ∠1 = ∠A + ∠B,∠2 = ∠C + ∠D,∠3 = ∠E + ∠F;
∴ ∠ A +∠ B +∠ C +∠ D +∠ E +∠ F = ∠ 1 + ∠ 2 + ∠ 3 ;
又 ∠ 1 + ∠ 2 + ∠ 3 是 △PMN 的外角和;
∴ ∠ A +∠ B +∠ C +∠ D +∠ E +∠ F = ∠ 1 + ∠ 2 + ∠ 3 = 360°
例 2:如图,试求出 ∠A + ∠B + ∠C + ∠D + ∠E + ∠F = ________.
360°
典型例题
3. 如图,已知三角形的两个外角 ∠1 = 125°、 ∠2 = 100°,则 ∠3 的度数为( )
A. 115° B. 125°
C. 135° D. 360°
【当堂检测】
C
1
2
3
B
C
A
四、课堂总结
三角形的外角
性质 1:
三角形的一个外角等于与它不相邻的两个内角的和;
外角和:三角形的外角和为 360°;
性质 2:
三角形的一个外角大于任何一个与它不相邻的内角;
