9.1.3 三角形的三边关系 课件(共15张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 9.1.3 三角形的三边关系 课件(共15张PPT) 2023-2024学年初中数学华东师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览




文档简介
(共15张PPT)
第九章 多边形
9.1 三角形
9.1.3 三角形的三边关系
一、学习目标
1.了解三角形的稳定性;
2.能证明三角形的任意两边之和大于第三边及其推论;
3.应用三角形的三边关系解决一些简单的问题; (重点)
二、新课导入
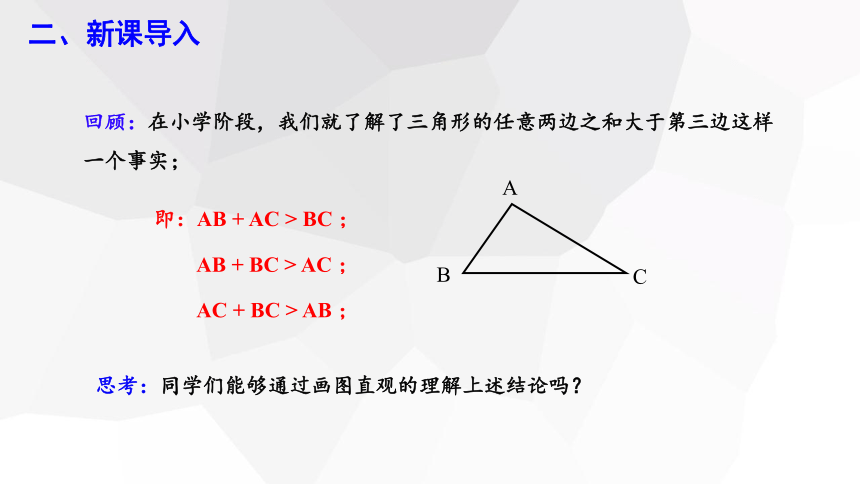
回顾:在小学阶段,我们就了解了三角形的任意两边之和大于第三边这样一个事实;
即:AB + AC > BC ;
思考:同学们能够通过画图直观的理解上述结论吗?
A
B
C
AB + BC > AC ;
AC + BC > AB ;
三、概念剖析
(一)三角形的三边关系
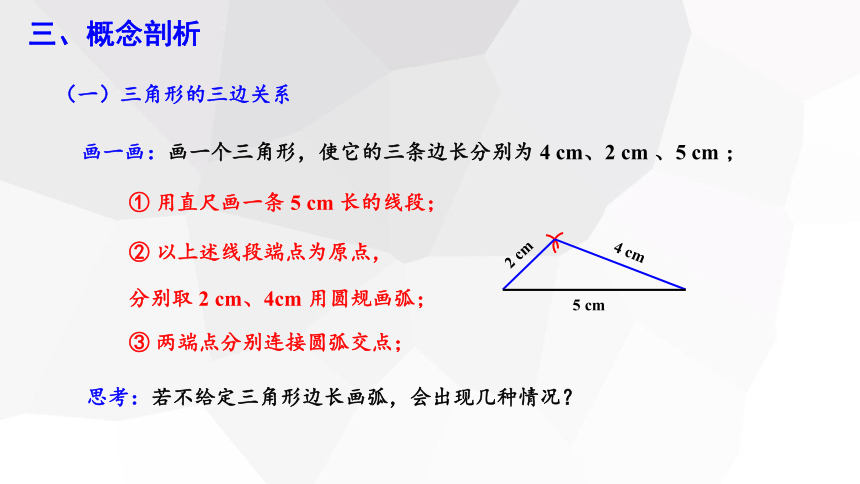
画一画:画一个三角形,使它的三条边长分别为 4 cm、2 cm 、5 cm ;
① 用直尺画一条 5 cm 长的线段;
思考:若不给定三角形边长画弧,会出现几种情况?
② 以上述线段端点为原点,
分别取 2 cm、4cm 用圆规画弧;
③ 两端点分别连接圆弧交点;
4 cm
2 cm
5 cm
三、概念剖析
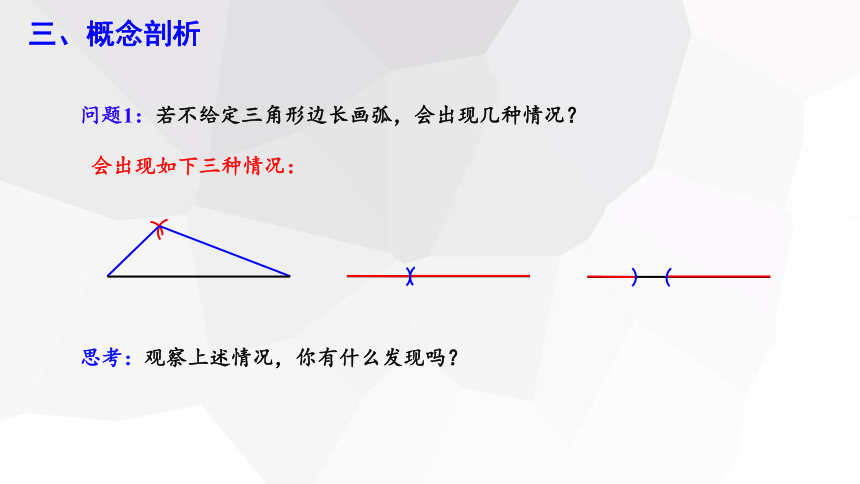
问题1:若不给定三角形边长画弧,会出现几种情况?
会出现如下三种情况:
思考:观察上述情况,你有什么发现吗?
三、概念剖析
发现:
(1)并不是任意三条线段都可组成三角形;
(2)只有当任意两条线段之和大于第三条线段时,才能组成三角形;
结论:三角形中任意两边的和大于第三边 .
推论:三角形中任意两边的差小于第三边(不等式的性质1) .
例 1:一个三角形的三边长分别为 3,8,x,求 x 的取值范围.
典型例题
分析:根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,即可解答.
列出不等式组: 8–3 < x < 8 + 3;
即 5 < x < 11;
故 x 的取值范围为: 5 < x < 11.
解:已知:三角形的三边长分别为 3,8,x;
注意:判断三角形边的取值范围:要同时运用两边之和大于第三边,两边之差小于第三边.
【当堂检测】
1. 判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;(3)5cm、6cm、10cm.
分析:根据三角形的三边关系判断即可;
解:(1)不能;因为 3 cm + 4 cm < 8 cm;
(2)不能;因为 5 cm + 6 cm = 11 cm;
(3)能;因为 5 cm + 6 cm > 10 cm.
注意:判断三角形的三边关系只要有一个不满足即可判断不能组成三角形.
【当堂检测】
2. 用一条长为18 cm 的细绳围成一个三角形. 已知该三角形的两边长为 x 和 2x ;若该三角形的边长均为整数,求 x 的值.
解:已知两边长为 x 和 2x ,则第三边长为 (18 – 3x) ;
根据三角形的三边关系列出不等式得:
x + 2x > 18 – 3x , 2x – x < 18 – 3x;
解得 3 < x < 4.5;
因为 x 为整数,故 x = 4 .
三、概念剖析
(二)三角形的稳定性
概念 1:如果三角形三条边的三条边固定,那么三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
思考:三角形的稳定性在生活中有什么实际应用?
误区警示:三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形的三条边确定,其形状和大小就确定了”.
三、概念剖析
三角形的稳定性在实际生活中的应用
例 2:如图,工人师傅砌门时,常用木条EF、EG固定门框ABCD,使其不变形,这种做法的根据是什么?
分析:利用的是三角形的稳定性;
当增加的木条EF、EG位置确定时,△AEG和△DEF的三条边都确定了长度,两个三角形的形状和大小就完全确定;
根据三角形的稳定性,这两个三角形会很稳固.
B
A
E
F
C
D
G
典型例题
【当堂检测】
3. 判断下列图形中哪些具有稳定性.
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
具有稳定性
不具有稳定性
4. 如图,桥梁的斜拉钢索是三角形的结构,主要是为了 ( )
A. 节省材料,节约成本
B. 保持对称
C. 利用三角形的稳定性
D. 美观漂亮
C
【当堂检测】
五、课堂总结
三角形
任意两边之差小于第三边;
任意两边之和大于第三边;
三角形的稳定性
三角形的三边关系
第九章 多边形
9.1 三角形
9.1.3 三角形的三边关系
一、学习目标
1.了解三角形的稳定性;
2.能证明三角形的任意两边之和大于第三边及其推论;
3.应用三角形的三边关系解决一些简单的问题; (重点)
二、新课导入
回顾:在小学阶段,我们就了解了三角形的任意两边之和大于第三边这样一个事实;
即:AB + AC > BC ;
思考:同学们能够通过画图直观的理解上述结论吗?
A
B
C
AB + BC > AC ;
AC + BC > AB ;
三、概念剖析
(一)三角形的三边关系
画一画:画一个三角形,使它的三条边长分别为 4 cm、2 cm 、5 cm ;
① 用直尺画一条 5 cm 长的线段;
思考:若不给定三角形边长画弧,会出现几种情况?
② 以上述线段端点为原点,
分别取 2 cm、4cm 用圆规画弧;
③ 两端点分别连接圆弧交点;
4 cm
2 cm
5 cm
三、概念剖析
问题1:若不给定三角形边长画弧,会出现几种情况?
会出现如下三种情况:
思考:观察上述情况,你有什么发现吗?
三、概念剖析
发现:
(1)并不是任意三条线段都可组成三角形;
(2)只有当任意两条线段之和大于第三条线段时,才能组成三角形;
结论:三角形中任意两边的和大于第三边 .
推论:三角形中任意两边的差小于第三边(不等式的性质1) .
例 1:一个三角形的三边长分别为 3,8,x,求 x 的取值范围.
典型例题
分析:根据三角形的三边关系:两边之和大于第三边,两边之差小于第三边,即可解答.
列出不等式组: 8–3 < x < 8 + 3;
即 5 < x < 11;
故 x 的取值范围为: 5 < x < 11.
解:已知:三角形的三边长分别为 3,8,x;
注意:判断三角形边的取值范围:要同时运用两边之和大于第三边,两边之差小于第三边.
【当堂检测】
1. 判断下列长度的三条线段能否拼成三角形?为什么?
(1)3cm、8cm、4cm; (2)5cm、6cm、11cm;(3)5cm、6cm、10cm.
分析:根据三角形的三边关系判断即可;
解:(1)不能;因为 3 cm + 4 cm < 8 cm;
(2)不能;因为 5 cm + 6 cm = 11 cm;
(3)能;因为 5 cm + 6 cm > 10 cm.
注意:判断三角形的三边关系只要有一个不满足即可判断不能组成三角形.
【当堂检测】
2. 用一条长为18 cm 的细绳围成一个三角形. 已知该三角形的两边长为 x 和 2x ;若该三角形的边长均为整数,求 x 的值.
解:已知两边长为 x 和 2x ,则第三边长为 (18 – 3x) ;
根据三角形的三边关系列出不等式得:
x + 2x > 18 – 3x , 2x – x < 18 – 3x;
解得 3 < x < 4.5;
因为 x 为整数,故 x = 4 .
三、概念剖析
(二)三角形的稳定性
概念 1:如果三角形三条边的三条边固定,那么三角形的形状和大小也就完全确定,三角形的这种性质叫做“三角形的稳定性”.
思考:三角形的稳定性在生活中有什么实际应用?
误区警示:三角形的稳定性不是“拉得动、拉不动”的问题,其实质应是“三角形的三条边确定,其形状和大小就确定了”.
三、概念剖析
三角形的稳定性在实际生活中的应用
例 2:如图,工人师傅砌门时,常用木条EF、EG固定门框ABCD,使其不变形,这种做法的根据是什么?
分析:利用的是三角形的稳定性;
当增加的木条EF、EG位置确定时,△AEG和△DEF的三条边都确定了长度,两个三角形的形状和大小就完全确定;
根据三角形的稳定性,这两个三角形会很稳固.
B
A
E
F
C
D
G
典型例题
【当堂检测】
3. 判断下列图形中哪些具有稳定性.
具有稳定性
不具有稳定性
不具有稳定性
具有稳定性
具有稳定性
不具有稳定性
4. 如图,桥梁的斜拉钢索是三角形的结构,主要是为了 ( )
A. 节省材料,节约成本
B. 保持对称
C. 利用三角形的稳定性
D. 美观漂亮
C
【当堂检测】
五、课堂总结
三角形
任意两边之差小于第三边;
任意两边之和大于第三边;
三角形的稳定性
三角形的三边关系
