9.3.1 用相同的正多边形 课件(共15张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 9.3.1 用相同的正多边形 课件(共15张PPT) 2023-2024学年初中数学华东师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
第九章 多边形
9.3 用正多边形铺设地面
第1课时 用相同的正多边形
一、学习目标
1.知道用相同的正多边形铺设地面的条件;
2.能判断某种正多边形能否用来铺设地面.(重点)
二、新课导入
生活中的镶嵌
思考:在生活中有没有遇到正五边形的瓷砖铺成的地面或墙面?为什么?
三、概念剖析
(一)镶嵌的概念
镶嵌的定义:用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖;
从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖(不留缝隙),就叫做用多边形覆盖平面,或叫做平面镶嵌.
三、概念剖析
(二)镶嵌的条件
活动:用一种正多边形镶嵌平面.
思考:从一些边长相同的正三角形、正方形、正五边形、正六边形中,选择其中的一种进行平面镶嵌,哪几种正多边形能够镶嵌成平面图案?
我们发现能够镶嵌成平面图案的有:
不能镶嵌成平面图案的有:
正五边形
正三角形
正方形
正六边形
三、概念剖析
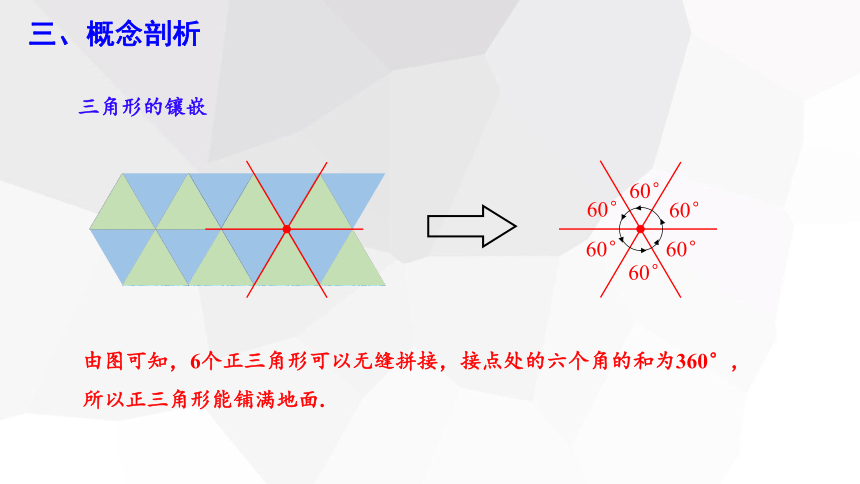
三角形的镶嵌
60°
60°
60°
60°
60°
60°
由图可知,6个正三角形可以无缝拼接,接点处的六个角的和为360°,
所以正三角形能铺满地面.
三、概念剖析
正方形的镶嵌
由图可知, 4个正方形可以无缝拼接,接点处的四个角的和为360°,
所以正方形能铺满地面.
90°
90°
90°
90°
三、概念剖析
正五边形的镶嵌
由图可知,正五边形不能无缝拼接,
接点处的角之和不等于360°,
所以正五边形不能铺满地面.
三、概念剖析
正六边形的镶嵌
由图可知,3个正六边形可以无缝拼接,接点处的三个角的和为360°,
所以正六边形能铺满地面.
120°
120°
120°
思考:结合上述结论,思考为什么六边形可以铺满地面而五边形不能?
思考:通过观察,能否铺满地面与正多边形的内角有何关系?
三、概念剖析
总结:使用给定的某种正多边形,当围绕一点拼在一起的几个内角相加在一起恰好组成一个 周角(360°)时,即正多边形的一个内角的整数倍等于360°时,就可以铺满地面.
例如:
正三角形
每个内角60°;6×60°= 360°
周角360°
三、概念剖析
例 1:现有六种地板砖,它们的形状分别是:正三角形、正方形、正五边形、
正六边形、正八边形、正十边形,如果只用一种地砖就能完成一个平面的镶嵌,选择的方式有哪几种?
四、典型例题
(一)用相同的正多边形铺设地面
分析:能够平面镶嵌的条件是它们内角的正整数倍等于 360°.
解:正三角形、正方形、正五边形、正六边形、正八边形、正十边形的内角度数分别是:60°、90°、108°、120°、135°、144°;
( 下接 )
四、典型例题
60°× 6 = 360° 正三角形能完成镶嵌;
90°× 4 = 360° 正方形能完成镶嵌;
120°× 3 = 360° 正六边形能完成镶嵌;
108°、135°、144°不是 360°的正整数倍, 因此正五边形、正八边形、
正十边形均不能完成镶嵌;
它们的内角度数:60°、90°、108°、120°、135°、144°;
答:选择的方式有3种,分别是:正三角形或正方形或正六边形镶嵌 .
【当堂检测】
1. 如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )
A. 正三角形 B. 正四边形 C. 正六边形 D. 正九边形
D
正多边形铺设地面:
2. 用相同的正多边形铺设地面的条件:一个内角的正整数倍是周角时;
1. 正多边形每个内角的度数: ;
3. 能用于铺设地面的同一种正多边形:正三角形、正四边形、正六边形.
五、课堂总结
第九章 多边形
9.3 用正多边形铺设地面
第1课时 用相同的正多边形
一、学习目标
1.知道用相同的正多边形铺设地面的条件;
2.能判断某种正多边形能否用来铺设地面.(重点)
二、新课导入
生活中的镶嵌
思考:在生活中有没有遇到正五边形的瓷砖铺成的地面或墙面?为什么?
三、概念剖析
(一)镶嵌的概念
镶嵌的定义:用地砖铺地,用瓷砖贴墙,都要求砖与砖严丝合缝,不留空隙,把地面或墙面全部覆盖;
从数学角度看,这些工作就是用一些不重叠摆放的多边形把平面的一部分完全覆盖(不留缝隙),就叫做用多边形覆盖平面,或叫做平面镶嵌.
三、概念剖析
(二)镶嵌的条件
活动:用一种正多边形镶嵌平面.
思考:从一些边长相同的正三角形、正方形、正五边形、正六边形中,选择其中的一种进行平面镶嵌,哪几种正多边形能够镶嵌成平面图案?
我们发现能够镶嵌成平面图案的有:
不能镶嵌成平面图案的有:
正五边形
正三角形
正方形
正六边形
三、概念剖析
三角形的镶嵌
60°
60°
60°
60°
60°
60°
由图可知,6个正三角形可以无缝拼接,接点处的六个角的和为360°,
所以正三角形能铺满地面.
三、概念剖析
正方形的镶嵌
由图可知, 4个正方形可以无缝拼接,接点处的四个角的和为360°,
所以正方形能铺满地面.
90°
90°
90°
90°
三、概念剖析
正五边形的镶嵌
由图可知,正五边形不能无缝拼接,
接点处的角之和不等于360°,
所以正五边形不能铺满地面.
三、概念剖析
正六边形的镶嵌
由图可知,3个正六边形可以无缝拼接,接点处的三个角的和为360°,
所以正六边形能铺满地面.
120°
120°
120°
思考:结合上述结论,思考为什么六边形可以铺满地面而五边形不能?
思考:通过观察,能否铺满地面与正多边形的内角有何关系?
三、概念剖析
总结:使用给定的某种正多边形,当围绕一点拼在一起的几个内角相加在一起恰好组成一个 周角(360°)时,即正多边形的一个内角的整数倍等于360°时,就可以铺满地面.
例如:
正三角形
每个内角60°;6×60°= 360°
周角360°
三、概念剖析
例 1:现有六种地板砖,它们的形状分别是:正三角形、正方形、正五边形、
正六边形、正八边形、正十边形,如果只用一种地砖就能完成一个平面的镶嵌,选择的方式有哪几种?
四、典型例题
(一)用相同的正多边形铺设地面
分析:能够平面镶嵌的条件是它们内角的正整数倍等于 360°.
解:正三角形、正方形、正五边形、正六边形、正八边形、正十边形的内角度数分别是:60°、90°、108°、120°、135°、144°;
( 下接 )
四、典型例题
60°× 6 = 360° 正三角形能完成镶嵌;
90°× 4 = 360° 正方形能完成镶嵌;
120°× 3 = 360° 正六边形能完成镶嵌;
108°、135°、144°不是 360°的正整数倍, 因此正五边形、正八边形、
正十边形均不能完成镶嵌;
它们的内角度数:60°、90°、108°、120°、135°、144°;
答:选择的方式有3种,分别是:正三角形或正方形或正六边形镶嵌 .
【当堂检测】
1. 如果仅用一种正多边形进行镶嵌,那么下列正多边形不能够将平面密铺的是( )
A. 正三角形 B. 正四边形 C. 正六边形 D. 正九边形
D
正多边形铺设地面:
2. 用相同的正多边形铺设地面的条件:一个内角的正整数倍是周角时;
1. 正多边形每个内角的度数: ;
3. 能用于铺设地面的同一种正多边形:正三角形、正四边形、正六边形.
五、课堂总结
