9.3.2 用多种正多边形 课件(共19张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 9.3.2 用多种正多边形 课件(共19张PPT) 2023-2024学年初中数学华东师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 541.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 07:51:54 | ||
图片预览





文档简介
(共19张PPT)
第九章 多边形
9.3 用正多边形铺设地面
第2课时 用多种正多边形
一、学习目标
1.能知道用多种正多边形铺设地面的条件;
2.能用多种正多边形进行简单的铺设地面设计.(重点)
二、新课导入
上节课我们学习了如何使用一种正多边形铺设地面,那么如果使用多种正多边形也能完成铺设吗?又该如何完成铺设?
三、概念剖析
(一)用多种正多边形铺设地面
问题1:从正三角形、正方形、正五边形、正六边形、正八边形、正十边形中任取几种进行组合是否能铺满地面呢?
两种正多边形:
正方形、正三角形:
三、概念剖析
两种正多边形:
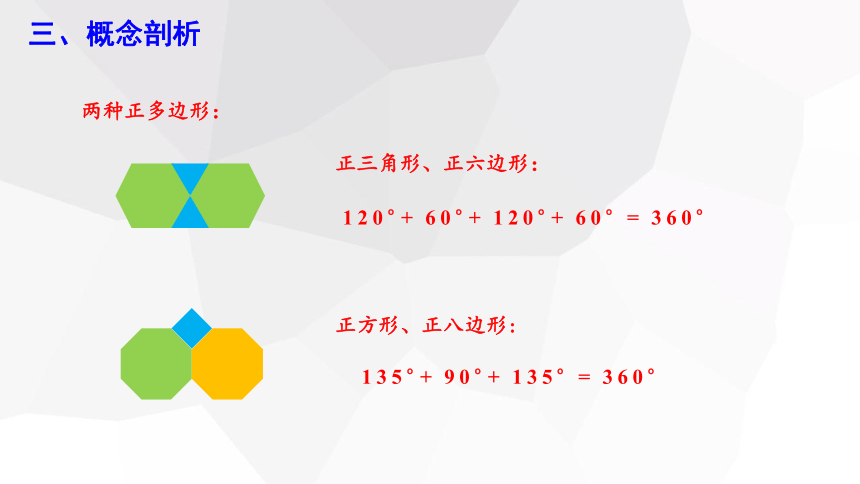
正三角形、正六边形:
正方形、正八边形:
三、概念剖析
两种正多边形:
正十边形、正五边形:
思考:围绕一点能拼成360 ,但能扩展到整个平面,即铺满地面吗?
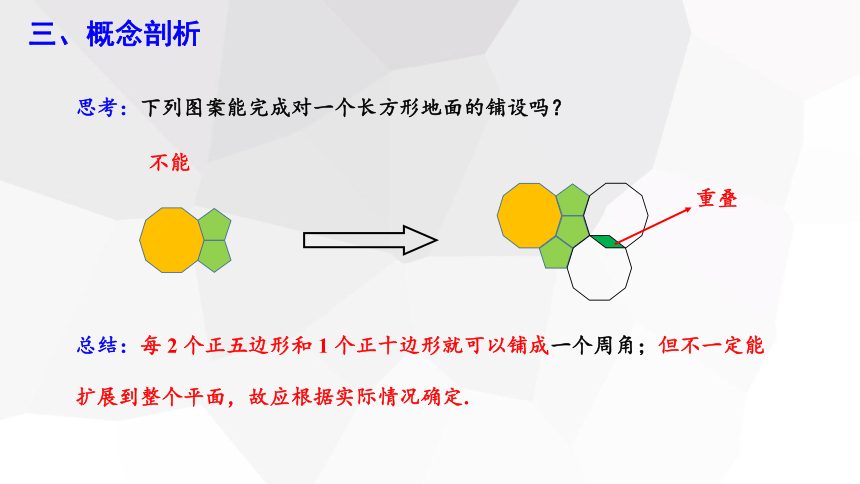
思考:下列图案能完成对一个长方形地面的铺设吗?
不能
总结:每 2 个正五边形和 1 个正十边形就可以铺成一个周角;但不一定能扩展到整个平面,故应根据实际情况确定.
重叠
三、概念剖析
三、概念剖析
三种多边形:
正六边形、正方形、正三角形:
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面;如:正五边形与正十边形的组合.
三、概念剖析
归纳总结:用多种正多边形铺设地面
关键:围绕一点拼在一起的多种正多边形的内角之和为360°;
模型:正多边形 1 的个数 × 正多边形 1 的内角度数 +
正多边形 2 的个数 × 正多边形 2 的内角度数 + … = 360 ;
例 1:现有形状分别为正三角形、正方形、正五边形、正六边形、正八边形、正十边形的地砖,如果同时选择两种地砖完成一个平面的镶嵌,选择的方式有哪几种?
四、典型例题
(一)用多种正多边形铺设地面
分析:完成平面镶嵌的条件是围绕一点拼在一起的多种正多边形的内角之和为360°;
正三角形、正方形、正五边形、正六边形、正八边形、正十边形的内角度数分别是:60°、90°、108°、120°、135°、144°;
四、典型例题
解:正三角形、正方形、正五边形、正六边形、正八边形、正十边形的内角度数分别是:60°、90°、108°、120°、135°、144°;
正三角形 + 正方形: 60°× 3 + 90°×2 = 360°;
正方形 + 正八边形: 90°×1 + 135°×2 = 360°;
答:选择的方式有4种,分别是:正三角形 + 正方形,正三角形 + 正
六边形,正方形 + 正八边形,正三角形 + 正十二边形.
正三角形 + 正六边形: 60°× 4 + 120°×1 = 360°;
正三角形 + 正十二边形: 60°×1 + 150°×2 = 360°.
总结:
平面镶嵌的原则:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角;
用正多边形进行平面镶嵌的常用方法:
(1)只用一种正多边形;(2)同时用两种正多边形;
四、典型例题
1. 现有边长相同的正三角形、正方形和正六边形纸片若干张,下列拼法中不能铺满一个平面图案的是 ( )
A. 正方形和正六边形 B. 正三角形和正方形
C. 正三角形和正六边形 D. 正三角形、正方形和正六边形
A
【当堂检测】
2. 有以下四组多边形地板砖:①正三角形与正方形;②正三角形与正六边形;
③正六边形与正方形;④正八边形与正方形. 将每组中的两种进行结合,能
密铺地面的是 ( )
A. ①③④ B. ②③④ C. ①②③ D. ①②④
D
【当堂检测】
例 2:如图所示的是一个长方形地面,现有正三角形、正方形和正六边形三种瓷砖若干,要求:① 三种瓷砖必须都用到;② 铺成长方形或近似长方形. 请你设计一种方案.
(二)用多种正多边形铺设地面的设计
分析:因为正三角形、正方形和正六边形
的每个内角分别是 60°、90°、120°;
根据 1×60°+ 2×90°+ 1×120°= 360°可得下图.
四、典型例题
解:如图所示,因为三种瓷砖都必须用到,所以在每一个顶点处放正三角形1个,正方形2个,正六边形1个即可.
四、典型例题
3. 为了美化城市,建设中的某小广场准备用边长相等的正三角形和正四边形两种地砖镶嵌地面,在每一个顶点周围,正三角形、正四边形地砖的块数分别是 ( )
A. 1,2 B. 2,1 C. 2,3 D. 3,2
D
【当堂检测】
4. 现有四种地板砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等. 同时选择其中两种密铺地面,选择的方式有 ( )
A. 2种 B. 3种 C. 4种 D. 5种
B
【当堂检测】
五、课堂总结
2. 用多种正多边形:如三个正三角形和两个正方形等.
1. 用相同的正多边形:正三角形、正四边形、正六边形;
用多边形铺设地面:
第九章 多边形
9.3 用正多边形铺设地面
第2课时 用多种正多边形
一、学习目标
1.能知道用多种正多边形铺设地面的条件;
2.能用多种正多边形进行简单的铺设地面设计.(重点)
二、新课导入
上节课我们学习了如何使用一种正多边形铺设地面,那么如果使用多种正多边形也能完成铺设吗?又该如何完成铺设?
三、概念剖析
(一)用多种正多边形铺设地面
问题1:从正三角形、正方形、正五边形、正六边形、正八边形、正十边形中任取几种进行组合是否能铺满地面呢?
两种正多边形:
正方形、正三角形:
三、概念剖析
两种正多边形:
正三角形、正六边形:
正方形、正八边形:
三、概念剖析
两种正多边形:
正十边形、正五边形:
思考:围绕一点能拼成360 ,但能扩展到整个平面,即铺满地面吗?
思考:下列图案能完成对一个长方形地面的铺设吗?
不能
总结:每 2 个正五边形和 1 个正十边形就可以铺成一个周角;但不一定能扩展到整个平面,故应根据实际情况确定.
重叠
三、概念剖析
三、概念剖析
三种多边形:
正六边形、正方形、正三角形:
注:有时几种正多边形的组合能围绕一点拼成周角,但不能扩展到整个平面,即不能铺满平面;如:正五边形与正十边形的组合.
三、概念剖析
归纳总结:用多种正多边形铺设地面
关键:围绕一点拼在一起的多种正多边形的内角之和为360°;
模型:正多边形 1 的个数 × 正多边形 1 的内角度数 +
正多边形 2 的个数 × 正多边形 2 的内角度数 + … = 360 ;
例 1:现有形状分别为正三角形、正方形、正五边形、正六边形、正八边形、正十边形的地砖,如果同时选择两种地砖完成一个平面的镶嵌,选择的方式有哪几种?
四、典型例题
(一)用多种正多边形铺设地面
分析:完成平面镶嵌的条件是围绕一点拼在一起的多种正多边形的内角之和为360°;
正三角形、正方形、正五边形、正六边形、正八边形、正十边形的内角度数分别是:60°、90°、108°、120°、135°、144°;
四、典型例题
解:正三角形、正方形、正五边形、正六边形、正八边形、正十边形的内角度数分别是:60°、90°、108°、120°、135°、144°;
正三角形 + 正方形: 60°× 3 + 90°×2 = 360°;
正方形 + 正八边形: 90°×1 + 135°×2 = 360°;
答:选择的方式有4种,分别是:正三角形 + 正方形,正三角形 + 正
六边形,正方形 + 正八边形,正三角形 + 正十二边形.
正三角形 + 正六边形: 60°× 4 + 120°×1 = 360°;
正三角形 + 正十二边形: 60°×1 + 150°×2 = 360°.
总结:
平面镶嵌的原则:围绕一点拼在一起的多边形的内角加在一起恰好组成一个周角;
用正多边形进行平面镶嵌的常用方法:
(1)只用一种正多边形;(2)同时用两种正多边形;
四、典型例题
1. 现有边长相同的正三角形、正方形和正六边形纸片若干张,下列拼法中不能铺满一个平面图案的是 ( )
A. 正方形和正六边形 B. 正三角形和正方形
C. 正三角形和正六边形 D. 正三角形、正方形和正六边形
A
【当堂检测】
2. 有以下四组多边形地板砖:①正三角形与正方形;②正三角形与正六边形;
③正六边形与正方形;④正八边形与正方形. 将每组中的两种进行结合,能
密铺地面的是 ( )
A. ①③④ B. ②③④ C. ①②③ D. ①②④
D
【当堂检测】
例 2:如图所示的是一个长方形地面,现有正三角形、正方形和正六边形三种瓷砖若干,要求:① 三种瓷砖必须都用到;② 铺成长方形或近似长方形. 请你设计一种方案.
(二)用多种正多边形铺设地面的设计
分析:因为正三角形、正方形和正六边形
的每个内角分别是 60°、90°、120°;
根据 1×60°+ 2×90°+ 1×120°= 360°可得下图.
四、典型例题
解:如图所示,因为三种瓷砖都必须用到,所以在每一个顶点处放正三角形1个,正方形2个,正六边形1个即可.
四、典型例题
3. 为了美化城市,建设中的某小广场准备用边长相等的正三角形和正四边形两种地砖镶嵌地面,在每一个顶点周围,正三角形、正四边形地砖的块数分别是 ( )
A. 1,2 B. 2,1 C. 2,3 D. 3,2
D
【当堂检测】
4. 现有四种地板砖,它们的形状分别是:正三角形、正方形、正六边形、正八边形,且它们的边长都相等. 同时选择其中两种密铺地面,选择的方式有 ( )
A. 2种 B. 3种 C. 4种 D. 5种
B
【当堂检测】
五、课堂总结
2. 用多种正多边形:如三个正三角形和两个正方形等.
1. 用相同的正多边形:正三角形、正四边形、正六边形;
用多边形铺设地面:
