10.3.2 旋转的特征 课件(共13张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 10.3.2 旋转的特征 课件(共13张PPT) 2023-2024学年初中数学华东师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 417.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 08:32:06 | ||
图片预览





文档简介
(共13张PPT)
10.3 旋转
第2课时 旋转的特征
第十章 轴对称、平移与旋转
一、学习目标
1.能掌握旋转的特征.
2.会用旋转的特征解决简单的数学问题
二、新课导入
回顾
什么是旋转?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度的运动叫做图形的旋转,简称旋转.
图形的旋转由什么所决定
由旋转中心、旋转角度和旋转方向所决定.
三、概念剖析
如图,△AOB绕点O旋转得到△ A'OB',
OA=OA', OB=OB', AB=A'B'
∠AOA'=∠BOB′
∠OA'B'=∠OAB,∠A'B'O=∠ABO,∠A'OB'=∠AOB
通过上节课的学习,我们已经知道了图中的对应点,对应线,对应角以及旋转角度,
除此之外,你还能发现哪些线段相等?哪些角相等呢?
三、概念剖析
联想平移的特征你能概括出旋转的特征吗?
图形旋转的特征:
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小不变.
典型例题
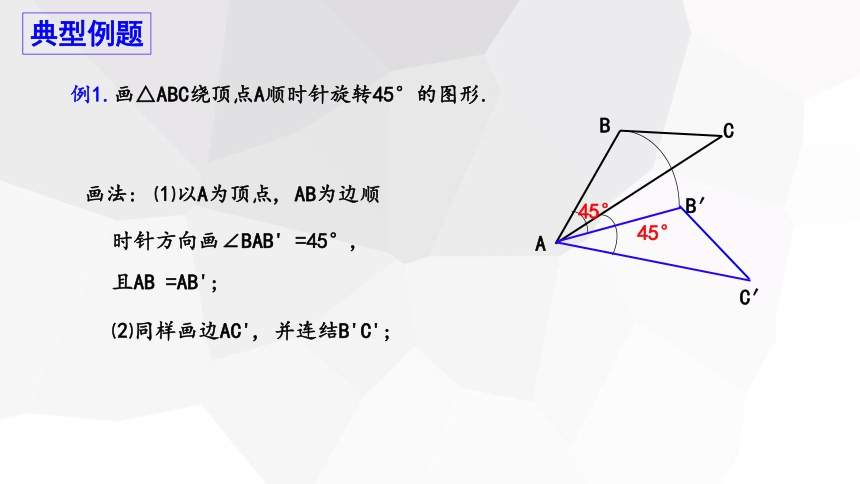
例1.画△ABC绕顶点A顺时针旋转45°的图形.
A
B
C
B′
C′
画法:
45°
⑴以A为顶点, AB为边顺
时针方向画∠BAB' =45°,
且AB =AB';
⑵同样画边AC', 并连结B'C';
45°
【当堂检测】
1.画出△ABC绕点C逆时针旋转90°后的图形.
A
C
B
B'
A'
2.如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,画出△ACE以点A为旋转中心、逆时针方向旋转90°后的三角形.
【当堂检测】
解:∵△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,
∴EA绕A点逆时针旋转后的对应边是AB,AC绕A点逆时针旋转后的对应边是AD,
∵旋转后图形的形状与大小不变,
∴连接BD,△ABD即为旋转后的图形.
典型例题
例2.已知直角△ABC中, ∠ACB=90°, ∠A=35°,以直角顶点C为旋转中心, 将△ABC旋转到△DEC的位置,斜边DE恰好过点B,直角边CD交AB于O, 求∠BOC的度数.
A
C
B
D
E
O
35°
解:∵BC与EC是对应边,∠E与∠CBA是对应角
∴BC=EC,∠E=∠CBA=∠EBC
∵∠ACB=90°, ∠A=35°
∴∠E=∠CBA=∠EBC=55°
∴∠BC0=20°
∴∠ECB=70°,
∴∠B0C=180°-20°-55°=105°
【当堂检测】
3.如图,把△ABC绕点A顺时针旋转46 得△ADE,点E恰好在BC边上,则∠C=______度.
67
E
A
B
C
D
4.如图,训练场上,士兵小王在射击完毕后,发现子弹集中在靶子的阴影部分,则阴影部分的面积为_______.(设靶子面积为S)
【当堂检测】
解析:根据旋转的特征求解
O
【当堂检测】
5.如图所示, △ABC是直角三角形, BC是斜边, △ABP绕点A逆时针旋转后,能与△ACP′重合,试判断△APP′的形状.
解:∵△ABC是直角三角形, BC是斜边,
∴△ACP′的旋转角度是90°,
P′
C
B
A
P
又∵AP与AP'是对应线段
∴AP=AP',
∴△APP′是等腰直角三角形.
四、课堂总结
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小不变.
图形旋转的特征:
10.3 旋转
第2课时 旋转的特征
第十章 轴对称、平移与旋转
一、学习目标
1.能掌握旋转的特征.
2.会用旋转的特征解决简单的数学问题
二、新课导入
回顾
什么是旋转?
在平面内,将一个图形绕着一个定点沿某个方向转动一个角度的运动叫做图形的旋转,简称旋转.
图形的旋转由什么所决定
由旋转中心、旋转角度和旋转方向所决定.
三、概念剖析
如图,△AOB绕点O旋转得到△ A'OB',
OA=OA', OB=OB', AB=A'B'
∠AOA'=∠BOB′
∠OA'B'=∠OAB,∠A'B'O=∠ABO,∠A'OB'=∠AOB
通过上节课的学习,我们已经知道了图中的对应点,对应线,对应角以及旋转角度,
除此之外,你还能发现哪些线段相等?哪些角相等呢?
三、概念剖析
联想平移的特征你能概括出旋转的特征吗?
图形旋转的特征:
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小不变.
典型例题
例1.画△ABC绕顶点A顺时针旋转45°的图形.
A
B
C
B′
C′
画法:
45°
⑴以A为顶点, AB为边顺
时针方向画∠BAB' =45°,
且AB =AB';
⑵同样画边AC', 并连结B'C';
45°
【当堂检测】
1.画出△ABC绕点C逆时针旋转90°后的图形.
A
C
B
B'
A'
2.如图,△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,画出△ACE以点A为旋转中心、逆时针方向旋转90°后的三角形.
【当堂检测】
解:∵△ACD、△AEB都是等腰直角三角形,∠CAD=∠EAB=90°,
∴EA绕A点逆时针旋转后的对应边是AB,AC绕A点逆时针旋转后的对应边是AD,
∵旋转后图形的形状与大小不变,
∴连接BD,△ABD即为旋转后的图形.
典型例题
例2.已知直角△ABC中, ∠ACB=90°, ∠A=35°,以直角顶点C为旋转中心, 将△ABC旋转到△DEC的位置,斜边DE恰好过点B,直角边CD交AB于O, 求∠BOC的度数.
A
C
B
D
E
O
35°
解:∵BC与EC是对应边,∠E与∠CBA是对应角
∴BC=EC,∠E=∠CBA=∠EBC
∵∠ACB=90°, ∠A=35°
∴∠E=∠CBA=∠EBC=55°
∴∠BC0=20°
∴∠ECB=70°,
∴∠B0C=180°-20°-55°=105°
【当堂检测】
3.如图,把△ABC绕点A顺时针旋转46 得△ADE,点E恰好在BC边上,则∠C=______度.
67
E
A
B
C
D
4.如图,训练场上,士兵小王在射击完毕后,发现子弹集中在靶子的阴影部分,则阴影部分的面积为_______.(设靶子面积为S)
【当堂检测】
解析:根据旋转的特征求解
O
【当堂检测】
5.如图所示, △ABC是直角三角形, BC是斜边, △ABP绕点A逆时针旋转后,能与△ACP′重合,试判断△APP′的形状.
解:∵△ABC是直角三角形, BC是斜边,
∴△ACP′的旋转角度是90°,
P′
C
B
A
P
又∵AP与AP'是对应线段
∴AP=AP',
∴△APP′是等腰直角三角形.
四、课堂总结
图形中每一点都绕着旋转中心按同一旋转方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,对应角相等,图形的形状和大小不变.
图形旋转的特征:
