10.5 图形的全等 课件(共15张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 10.5 图形的全等 课件(共15张PPT) 2023-2024学年初中数学华东师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 504.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 08:33:21 | ||
图片预览



文档简介
(共15张PPT)
第10章 轴对称、平移与旋转
10.5 图形的全等
一、学习目标
1.理解全等图形的概念,会区分所给图形是否是全等图形;
2.能找出全等图形的对应元素;
3.能应用全等图形的性质解决简单的数学问题.
二、新课导入
世界上没有完全相同的两片树叶,也没有完全相同的两个人.
但在生活中却经常能看到形状大小完全相同的图形,你能举一些的例子吗?
同一种剪纸
同一套邮票
三、概念剖析
(一)全等图形与全等三角形
试一试:把手中三角板按在纸上,画出三角形,并裁下来,把三角板和纸三角形放在一起,观察它们能够重合吗?
思考:把你的数学课本和同桌数学课本叠放在一起会重合吗?
发现:纸三角形和三角板完全重合.
三、概念剖析
发现:通过以上的实践活动,我们发现形状、大小相同的图形放在一起能
够完全重合;
概念总结:能够完全重合的两个图形就叫全等图形;
推论:能够完全重合的两个三角形就叫全等三角形.
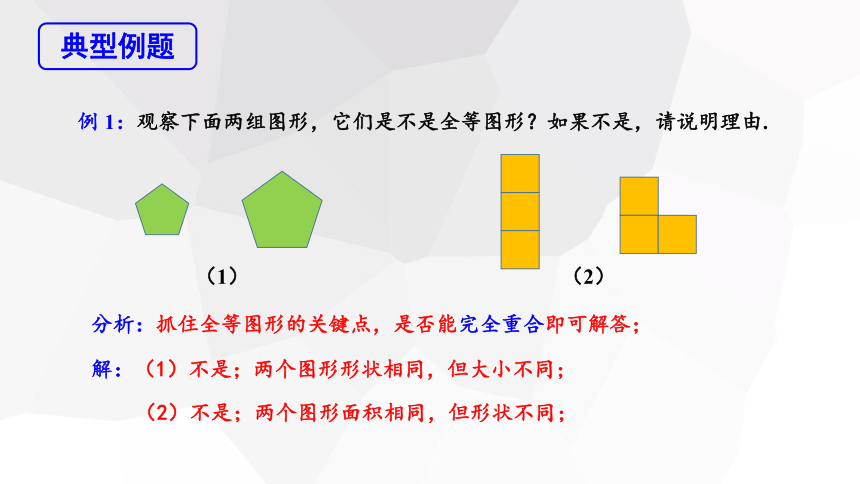
例 1:观察下面两组图形,它们是不是全等图形?如果不是,请说明理由.
典型例题
分析:抓住全等图形的关键点,是否能完全重合即可解答;
解:(1)不是;两个图形形状相同,但大小不同;
(2)不是;两个图形面积相同,但形状不同;
(2)
(1)
【当堂检测】
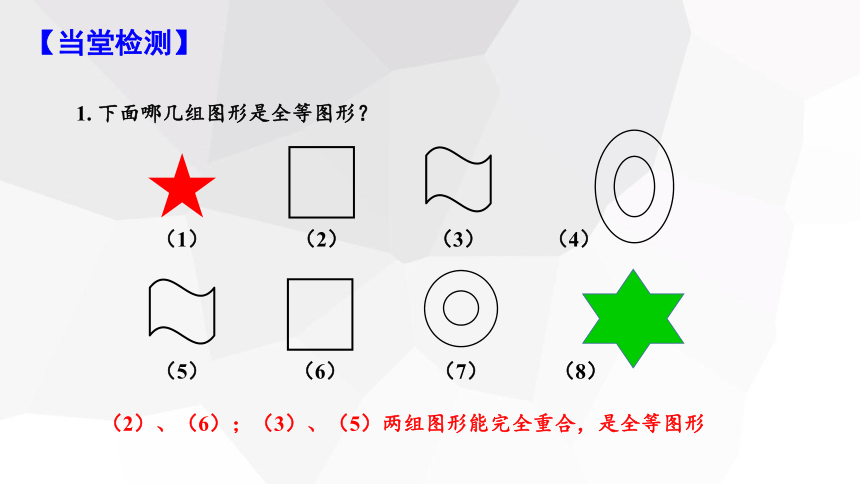
1. 下面哪几组图形是全等图形?
(1)
(2)
(3)
(4)
(8)
(7)
(5)
(6)
(2)、(6);(3)、(5)两组图形能完全重合,是全等图形
三、概念剖析
(二)全等图形的性质
问题 1:如果将两个全等三角形分别标为△ABC、△DEF,这两个三角形会有什么对应关系呢?
A
B
C
D
E
F
点A与点D、点B与点E、点C与点F 重合,称为对应顶点;
边AB与DE、边BC与EF、边AC与DF 重合,称为对应边;
∠A与∠D、∠B与∠E、∠C与∠F 重合,称为对应角.
三、概念剖析
A
B
C
D
E
F
总结:
在两个全等的三角形中,重合的顶点称为对应顶点,重合的边称为对应边,重合的角称为对应角.
三、概念剖析
为了方便书写,我们可以用符号表示两个三角形的全等.
例如:△ABC与△DEF 是全等的;
可以记作:“△ABC ≌ △DEF ”;
读作:“△ABC全等于△DEF ”;
注意:记两个三角形全等时,通常把对应顶点的字母写在对应位置上;
例如:△ABC与△DEF全等,点A 与点D、点B 与点E、点C 与点F为对应
顶点,记作“△ABC ≌△DEF ”.
A
B
C
D
E
F
三、概念剖析
问题 2:若将一对自制的全等三角形纸片重合,你发现了对应边、对应角之间的关系吗?
相等
思考:若一对多边形的对应边、对应角分别相等,那么它们是全等的吗?
是全等的
归纳总结
(1)全等多边形(三角形)的性质:
全等多边形(三角形)的对应边、对应角分别相等;
(2)全等多边形(三角形)的判定方法:
如果两个多边形(三角形)的边、角分别对应相等,那么这两个多边形全等.
三、概念剖析
例 2:如图,已知△ABC ≌ △DEF,∠A = 85°,∠B = 60°,AB = 8,EF = 5,求 ∠DFE 的度数与 DE 的长.
分析:根据全等三角形对应边、角都相等,再结合已知求解即可;
典型例题
又在 △ABC 中∠A = 85°,∠B = 60°,
解: 已知△ABC≌△DEF,
即∠DFE = ∠ACB,DE = AB = 8;
则 ∠ACB = 180°– 85°– 60°= 35°.
故∠DFE = 35 °.
【当堂检测】
3. 如图,△ABC ≌ △EDB,AC = 6,AB = 8,则 AE = .
A
B
E
D
C
2
四、课堂总结
第10章 轴对称、平移与旋转
10.5 图形的全等
一、学习目标
1.理解全等图形的概念,会区分所给图形是否是全等图形;
2.能找出全等图形的对应元素;
3.能应用全等图形的性质解决简单的数学问题.
二、新课导入
世界上没有完全相同的两片树叶,也没有完全相同的两个人.
但在生活中却经常能看到形状大小完全相同的图形,你能举一些的例子吗?
同一种剪纸
同一套邮票
三、概念剖析
(一)全等图形与全等三角形
试一试:把手中三角板按在纸上,画出三角形,并裁下来,把三角板和纸三角形放在一起,观察它们能够重合吗?
思考:把你的数学课本和同桌数学课本叠放在一起会重合吗?
发现:纸三角形和三角板完全重合.
三、概念剖析
发现:通过以上的实践活动,我们发现形状、大小相同的图形放在一起能
够完全重合;
概念总结:能够完全重合的两个图形就叫全等图形;
推论:能够完全重合的两个三角形就叫全等三角形.
例 1:观察下面两组图形,它们是不是全等图形?如果不是,请说明理由.
典型例题
分析:抓住全等图形的关键点,是否能完全重合即可解答;
解:(1)不是;两个图形形状相同,但大小不同;
(2)不是;两个图形面积相同,但形状不同;
(2)
(1)
【当堂检测】
1. 下面哪几组图形是全等图形?
(1)
(2)
(3)
(4)
(8)
(7)
(5)
(6)
(2)、(6);(3)、(5)两组图形能完全重合,是全等图形
三、概念剖析
(二)全等图形的性质
问题 1:如果将两个全等三角形分别标为△ABC、△DEF,这两个三角形会有什么对应关系呢?
A
B
C
D
E
F
点A与点D、点B与点E、点C与点F 重合,称为对应顶点;
边AB与DE、边BC与EF、边AC与DF 重合,称为对应边;
∠A与∠D、∠B与∠E、∠C与∠F 重合,称为对应角.
三、概念剖析
A
B
C
D
E
F
总结:
在两个全等的三角形中,重合的顶点称为对应顶点,重合的边称为对应边,重合的角称为对应角.
三、概念剖析
为了方便书写,我们可以用符号表示两个三角形的全等.
例如:△ABC与△DEF 是全等的;
可以记作:“△ABC ≌ △DEF ”;
读作:“△ABC全等于△DEF ”;
注意:记两个三角形全等时,通常把对应顶点的字母写在对应位置上;
例如:△ABC与△DEF全等,点A 与点D、点B 与点E、点C 与点F为对应
顶点,记作“△ABC ≌△DEF ”.
A
B
C
D
E
F
三、概念剖析
问题 2:若将一对自制的全等三角形纸片重合,你发现了对应边、对应角之间的关系吗?
相等
思考:若一对多边形的对应边、对应角分别相等,那么它们是全等的吗?
是全等的
归纳总结
(1)全等多边形(三角形)的性质:
全等多边形(三角形)的对应边、对应角分别相等;
(2)全等多边形(三角形)的判定方法:
如果两个多边形(三角形)的边、角分别对应相等,那么这两个多边形全等.
三、概念剖析
例 2:如图,已知△ABC ≌ △DEF,∠A = 85°,∠B = 60°,AB = 8,EF = 5,求 ∠DFE 的度数与 DE 的长.
分析:根据全等三角形对应边、角都相等,再结合已知求解即可;
典型例题
又在 △ABC 中∠A = 85°,∠B = 60°,
解: 已知△ABC≌△DEF,
即∠DFE = ∠ACB,DE = AB = 8;
则 ∠ACB = 180°– 85°– 60°= 35°.
故∠DFE = 35 °.
【当堂检测】
3. 如图,△ABC ≌ △EDB,AC = 6,AB = 8,则 AE = .
A
B
E
D
C
2
四、课堂总结
