第八章 一元一次不等式 复习课 课件(共24张PPT) 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 第八章 一元一次不等式 复习课 课件(共24张PPT) 2023-2024学年初中数学华东师大版七年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 217.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览








文档简介
(共24张PPT)
第八章 一元一次不等式
复习课
一、学习目标
1.掌握一元一次不等式(组)的概念和基本性质,会解一元一次不等式(组);(重点)
2.会用数轴表示一元一次不等式(组)的解集;
3.能根据具体问题中的数量关系,列出一元一次不等式(组)解决实际问题.(难点)
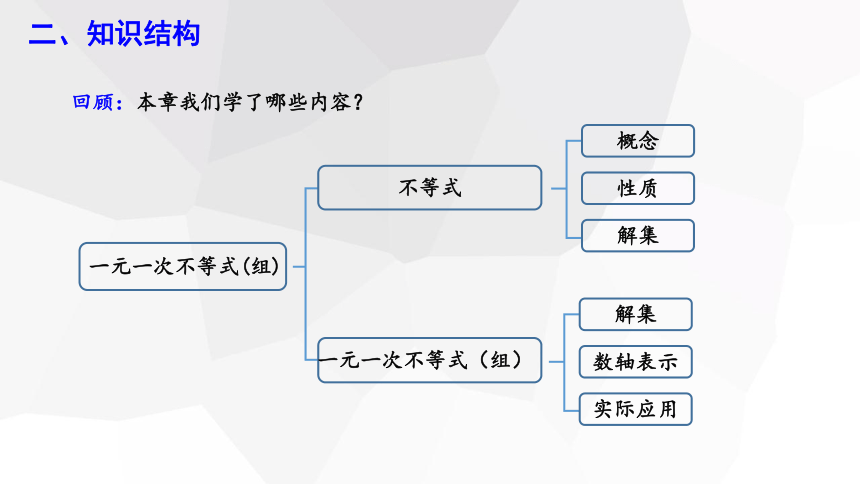
二、知识结构
回顾:本章我们学了哪些内容?
一元一次不等式(组)
不等式
一元一次不等式(组)
概念
性质
解集
解集
数轴表示
实际应用
1. 不等号有:“ > ”、“ ≥ ”、“ < ”、“ ≤ ” 或 “ ≠ ”;
一、不等式的有关概念
2. 不等式:用不等号表示不等关系的式子叫不等式 .
三、知识回顾
3. 不等式的基本性质:
性质1:如果a > b,那么 a + c > b + c,且 a – c > b – c;
不等式还具有传递性:如果 a > b,b > c,那么 a > c.
性质2:如果a > b,c > 0,那么 ac > bc, > ;
性质3:如果a > b,c < 0,那么 ac < bc, < ;
三、知识回顾
1. 一元一次不等式:只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数都是1.
二、一元一次不等式(组)的相关概念
2. 不等式的解:使不等式成立的未知数的值叫做不等式的解;
3. 不等式的解集:这些解的全体称为这个不等式的解集;
4. 解不等式:求不等式解集的过程叫解不等式.
三、知识回顾
5. 不等式组:几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不等式组;
6.不等式组的解集:这几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集.
三、知识回顾
1. 解一元一次不等式的一般步骤:
三、解一元一次不等式(组)
① 去分母;② 去括号;③ 移项;④ 合并同类项;⑤ 将未知数系数化为1.
注意:在上面步骤 ① 和 ⑤ 中,如果乘数或除数是负数,那么在利用不等式的 基本性质 3 时,一定要改变不等号的方向.
三、知识回顾
2. 解一元一次不等式组的一般步骤:
① 分别解每一个不等式;
② 在同一数轴上表示每个不等式的解集;
③ 找出各不等式解集的公共部分.
三、知识回顾
四、用数轴表示一元一次不等式(组)的解集
a
b
同大取大
x > b
a
b
同小取小
x < a
a
b
大小小大中间找
a < x < b
a
b
大大小小解不了
无解
三、知识回顾
五、利用一元一次不等式(组)解决实际问题
① 审: 找出题目中的不等关系;
② 设:设出未知数,用未知数表示有关代数式;
③ 列:列出不等式;
④ 解:解不等式;
⑤ 答:根据实际情况写出答案.
三、知识回顾
(一)运用不等式的基本性质求解
四、典型例题
分析:根据不等式的性质1:不等式的两边都加上(或减去)同一数或同一个整式,不等号的方向不变. 故A、B正确;
例1:若 a > b,则下列结论错误的是 ( )
A.a – 5 > b – 5 B.5 + a > b + 5
C. D.– 4a > – 4b
根据不等式的性质2:C正确;
根据不等式的基本性质3:D错误,应为 – 4a < – 4b.
D
四、典型例题
归纳总结
不等式变形的两点注意:
(1)一般要把不等式的右边化成常数,左边化成只含有未知数的形式,
(2)应用不等式的基本性质 3 时,要改变不等号的方向.
【当堂检测】
1. 已知 a < b,则下列各式不成立的是( )
A. 3a < 3b B. –3a < –3b
C. a – 3 < b – 3 D. 3 + a < 3 + b
B
2. 用“ > ”或“ < ”填空:
(1)如果 1 – x > 3,那么 – x 3 – 1,得 x –2;
(2)如果 x + 2 < 3x + 8,那么 x – 3x 8 – 2,即 – 2x 6,得 x – 3.
>
<
<
>
<
四、典型例题
(二)解一元一次不等式
例2:解不等式: ,并把解集表示在数轴上.
解:去分母得:2 ( 4 + x ) – 6 < 3x;
去括号得:8 + 2x – 6 < 3x;
移项得: 8 – 6 < 3x – 2x ;
合并同类项得:2 < x;
即:x > 2;
不等式的解集在数轴上表示如图所示:
– 1
0
1
2
3
4
归纳总结:
先求出不等式的解集,然后根据“大于向右画,小于向左画”在数轴上表示解集.
注:含等号用实心圆点,不含等号用空心圆圈.
四、典型例题
移项得:7x – 9x ≤ 3 + 2;
合并同类项得:–2x ≤ 5;
注意:系数化为1时,要注意不等号的方向.
3. 解不等式 7x – 2 ≤ 9x + 3,并把解集表示在数轴上.
解:7x – 2 ≤ 9x + 3;
系数化为 1 得:
不等式的解集在数轴上表示如图所示:
x ≥
– 2
– 1
0
1
2
3
– 3
【当堂检测】
四、典型例题
(三)解一元一次不等式组
解:由不等式 ① 得:x > 1;
分析:先分别解出每个不等式,再求出其公共部分即可.
由不等式 ② 得:x ≤ 5;
不等式的解集在数轴上表示如图所示:
例3:解不等式组 ,利用数轴确定不等式组的解集.
①
②
所以不等式组的解集为 1 < x ≤ 5 .
– 1
0
1
2
3
4
5
6
归纳总结
解一元一次不等式组的方法:
(1)分别求出不等式组中各个不等式的解集;
(2)利用数轴表示出不等式组中的各个不等式的解集;
(3)在数轴上找出各个不等式的解集的公共部分,即是这个不等式组的解集.
四、典型例题
4. 若关于 x 不等式组 有解,则 m 的取值范围为 ( )
A. m > B. m ≤ C. m > D. m ≤
C
【当堂检测】
四、典型例题
(四)用一元一次不等式(组)解决实际问题
例4:某小区计划购进甲、乙两种树苗,已知甲、乙两种树苗每株分别为8元、6元. 若购买甲、乙两种树苗共360株,并且甲树苗的数量不少于乙树苗的一半,请你设计一种费用最少的购买方案.
解:设购买甲树苗的数量为 x 株;
解得:x ≥ 120.
因为甲树苗比乙树苗每株多2元,
所以要节省费用,则要尽量少买甲树苗.
又因为x最小为120,
所以购买甲树苗120株,乙树苗240株,此时费用最省.
依题意得: ;
四、典型例题
归纳总结:
解不等式的应用问题的步骤包括审、设、列、解、找、答这几个环节;
在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.
5. 一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
【当堂检测】
解:设小朋友总共 x 人;
由此可得 5 < x ≤ 8;
因为 x 是整数,所以 x 可为 6、7、8.
答:小朋友有6人,玩具有22件;有7人,玩具有25件;有8人,玩具有28件.
3x + 4 – 4 ( x – 1 ) ≥ 0
3x + 4 – 4 ( x – 1 ) < 3
由此可得不等式组:
五、课堂总结
第八章 一元一次不等式
复习课
一、学习目标
1.掌握一元一次不等式(组)的概念和基本性质,会解一元一次不等式(组);(重点)
2.会用数轴表示一元一次不等式(组)的解集;
3.能根据具体问题中的数量关系,列出一元一次不等式(组)解决实际问题.(难点)
二、知识结构
回顾:本章我们学了哪些内容?
一元一次不等式(组)
不等式
一元一次不等式(组)
概念
性质
解集
解集
数轴表示
实际应用
1. 不等号有:“ > ”、“ ≥ ”、“ < ”、“ ≤ ” 或 “ ≠ ”;
一、不等式的有关概念
2. 不等式:用不等号表示不等关系的式子叫不等式 .
三、知识回顾
3. 不等式的基本性质:
性质1:如果a > b,那么 a + c > b + c,且 a – c > b – c;
不等式还具有传递性:如果 a > b,b > c,那么 a > c.
性质2:如果a > b,c > 0,那么 ac > bc, > ;
性质3:如果a > b,c < 0,那么 ac < bc, < ;
三、知识回顾
1. 一元一次不等式:只含有一个未知数,并且含有未知数的式子都是整式,未知数的次数都是1.
二、一元一次不等式(组)的相关概念
2. 不等式的解:使不等式成立的未知数的值叫做不等式的解;
3. 不等式的解集:这些解的全体称为这个不等式的解集;
4. 解不等式:求不等式解集的过程叫解不等式.
三、知识回顾
5. 不等式组:几个含有同一个未知数的一元一次不等式组成的不等式组,叫做一元一次不等式组;
6.不等式组的解集:这几个一元一次不等式解集的公共部分,叫做这个一元一次不等式组的解集.
三、知识回顾
1. 解一元一次不等式的一般步骤:
三、解一元一次不等式(组)
① 去分母;② 去括号;③ 移项;④ 合并同类项;⑤ 将未知数系数化为1.
注意:在上面步骤 ① 和 ⑤ 中,如果乘数或除数是负数,那么在利用不等式的 基本性质 3 时,一定要改变不等号的方向.
三、知识回顾
2. 解一元一次不等式组的一般步骤:
① 分别解每一个不等式;
② 在同一数轴上表示每个不等式的解集;
③ 找出各不等式解集的公共部分.
三、知识回顾
四、用数轴表示一元一次不等式(组)的解集
a
b
同大取大
x > b
a
b
同小取小
x < a
a
b
大小小大中间找
a < x < b
a
b
大大小小解不了
无解
三、知识回顾
五、利用一元一次不等式(组)解决实际问题
① 审: 找出题目中的不等关系;
② 设:设出未知数,用未知数表示有关代数式;
③ 列:列出不等式;
④ 解:解不等式;
⑤ 答:根据实际情况写出答案.
三、知识回顾
(一)运用不等式的基本性质求解
四、典型例题
分析:根据不等式的性质1:不等式的两边都加上(或减去)同一数或同一个整式,不等号的方向不变. 故A、B正确;
例1:若 a > b,则下列结论错误的是 ( )
A.a – 5 > b – 5 B.5 + a > b + 5
C. D.– 4a > – 4b
根据不等式的性质2:C正确;
根据不等式的基本性质3:D错误,应为 – 4a < – 4b.
D
四、典型例题
归纳总结
不等式变形的两点注意:
(1)一般要把不等式的右边化成常数,左边化成只含有未知数的形式,
(2)应用不等式的基本性质 3 时,要改变不等号的方向.
【当堂检测】
1. 已知 a < b,则下列各式不成立的是( )
A. 3a < 3b B. –3a < –3b
C. a – 3 < b – 3 D. 3 + a < 3 + b
B
2. 用“ > ”或“ < ”填空:
(1)如果 1 – x > 3,那么 – x 3 – 1,得 x –2;
(2)如果 x + 2 < 3x + 8,那么 x – 3x 8 – 2,即 – 2x 6,得 x – 3.
>
<
<
>
<
四、典型例题
(二)解一元一次不等式
例2:解不等式: ,并把解集表示在数轴上.
解:去分母得:2 ( 4 + x ) – 6 < 3x;
去括号得:8 + 2x – 6 < 3x;
移项得: 8 – 6 < 3x – 2x ;
合并同类项得:2 < x;
即:x > 2;
不等式的解集在数轴上表示如图所示:
– 1
0
1
2
3
4
归纳总结:
先求出不等式的解集,然后根据“大于向右画,小于向左画”在数轴上表示解集.
注:含等号用实心圆点,不含等号用空心圆圈.
四、典型例题
移项得:7x – 9x ≤ 3 + 2;
合并同类项得:–2x ≤ 5;
注意:系数化为1时,要注意不等号的方向.
3. 解不等式 7x – 2 ≤ 9x + 3,并把解集表示在数轴上.
解:7x – 2 ≤ 9x + 3;
系数化为 1 得:
不等式的解集在数轴上表示如图所示:
x ≥
– 2
– 1
0
1
2
3
– 3
【当堂检测】
四、典型例题
(三)解一元一次不等式组
解:由不等式 ① 得:x > 1;
分析:先分别解出每个不等式,再求出其公共部分即可.
由不等式 ② 得:x ≤ 5;
不等式的解集在数轴上表示如图所示:
例3:解不等式组 ,利用数轴确定不等式组的解集.
①
②
所以不等式组的解集为 1 < x ≤ 5 .
– 1
0
1
2
3
4
5
6
归纳总结
解一元一次不等式组的方法:
(1)分别求出不等式组中各个不等式的解集;
(2)利用数轴表示出不等式组中的各个不等式的解集;
(3)在数轴上找出各个不等式的解集的公共部分,即是这个不等式组的解集.
四、典型例题
4. 若关于 x 不等式组 有解,则 m 的取值范围为 ( )
A. m > B. m ≤ C. m > D. m ≤
C
【当堂检测】
四、典型例题
(四)用一元一次不等式(组)解决实际问题
例4:某小区计划购进甲、乙两种树苗,已知甲、乙两种树苗每株分别为8元、6元. 若购买甲、乙两种树苗共360株,并且甲树苗的数量不少于乙树苗的一半,请你设计一种费用最少的购买方案.
解:设购买甲树苗的数量为 x 株;
解得:x ≥ 120.
因为甲树苗比乙树苗每株多2元,
所以要节省费用,则要尽量少买甲树苗.
又因为x最小为120,
所以购买甲树苗120株,乙树苗240株,此时费用最省.
依题意得: ;
四、典型例题
归纳总结:
解不等式的应用问题的步骤包括审、设、列、解、找、答这几个环节;
在这些步骤中,最重要的是利用题中的已知条件,列出不等式(组),然后通过解出不等式(组)确定未知数的范围,利用未知数的特征(如整数问题),依据条件,找出对应的未知数的确定数值,以实现确定方案的解答.
5. 一堆玩具分给若干个小朋友,若每人分3件,则剩余4件;若前面每人分4件,则最后一人得到的玩具不足3件,求小朋友的人数与玩具数.
【当堂检测】
解:设小朋友总共 x 人;
由此可得 5 < x ≤ 8;
因为 x 是整数,所以 x 可为 6、7、8.
答:小朋友有6人,玩具有22件;有7人,玩具有25件;有8人,玩具有28件.
3x + 4 – 4 ( x – 1 ) ≥ 0
3x + 4 – 4 ( x – 1 ) < 3
由此可得不等式组:
五、课堂总结
