第十章 轴对称、平移与旋转 复习课 课件 21张PPT 2023-2024学年初中数学华东师大版七年级下册
文档属性
| 名称 | 第十章 轴对称、平移与旋转 复习课 课件 21张PPT 2023-2024学年初中数学华东师大版七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 651.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 08:45:59 | ||
图片预览








文档简介
(共21张PPT)
复习课
第十章 轴对称、平移与旋转
一、学习目标
1.理解图形经过轴对称、平移、旋转后能得到一个与原图形全等的图形;
2.会画简单图形经过轴对称、平移、旋转后的图形;
3.会用轴对称、平移、旋转、全等的性质解决简单的数学问题.
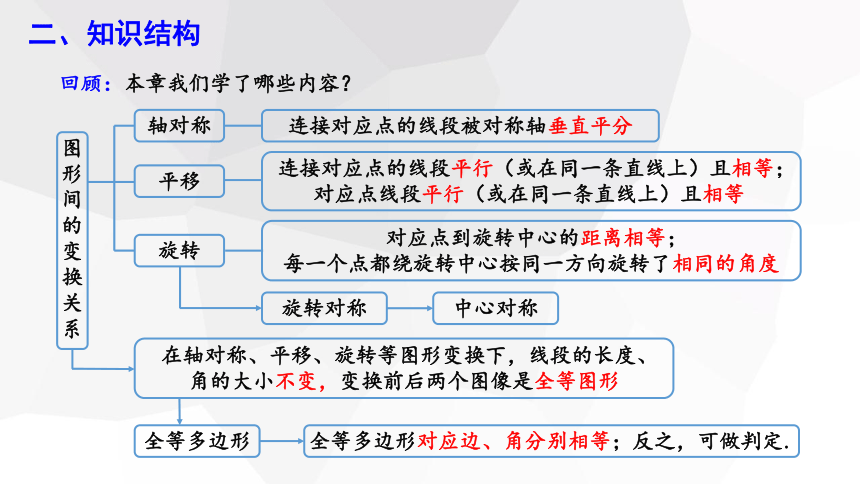
二、知识结构
回顾:本章我们学了哪些内容?
图形间的变换关系
轴对称
连接对应点的线段被对称轴垂直平分
平移
连接对应点的线段平行(或在同一条直线上)且相等;对应点线段平行(或在同一条直线上)且相等
旋转
对应点到旋转中心的距离相等;
每一个点都绕旋转中心按同一方向旋转了相同的角度
旋转对称
中心对称
在轴对称、平移、旋转等图形变换下,线段的长度、角的大小不变,变换前后两个图像是全等图形
全等多边形
全等多边形对应边、角分别相等;反之,可做判定.
一、轴对称
三、知识回顾
1. 轴对称图形:把一个图形沿某条直线对折,对折后两部分能完全重合,这个图形就是轴对称图形,这条直线即为这个图形的对称轴;
2. 轴对称:一个图形沿一条直线翻折,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点叫做对称点.
3. 轴对称图形的性质:轴对称图形(或成轴对称的两个图形)的对应线段相等,对应角相等;
4. 线段的垂直平分线:垂直并且平分一条线段的直线叫做这条线段的垂直平分线(或中垂线).
三、知识回顾
1. 平移:由移动的方向和距离所决定;
2. 平移的特征:平移后图形与原来图形的对应线段平行(或在同一直线上),并且相等;对应角相等,图形的形状与大小不变;
平移后对应点所连的线段平行 ( 或在同一直线上 ) 并且相等.
二、平移
三、知识回顾
1. 旋转:图形的旋转由旋转中心、旋转角度和旋转方向所决定;
2. 旋转的特征:图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,图形的形状与大小不变.
三、旋转
三、知识回顾
3. 旋转对称图形:旋转一定角度后能与自身重合的图形叫做旋转对称图形;
4. 中心对称图形:一个图形绕着中心旋转 180 度后能与自身重合,我们把这种图形叫做中心对称图形.
三、知识回顾
5. 中心对称的性质:在成中心对称的两个图形中,连结对称点的线段都经过 对称中心,并且被对称中心 平分;
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且被该点 平分,那么这两个图形关于这一点成 中心对称.
四、全等
三、知识回顾
1. 全等多边形的性质:全等多边形的对应边、对应角分别相等;
2. 全等多边形的判定:如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
(一)轴对称与轴对称图形
四、典型例题
例 1:观察图 ① ~ ④ 中的左右两个图形,它们是否成轴对称?如果是,请画出其对称轴.
分析:图 ① ② ③ 中的两个图形成轴对称;
图 ④ 中的两个图形不成轴对称;
图 ① ② ③ 中的对称轴如下图所示(下接).
注意:判断两个图形是否成轴对称,关键是理解、应用两个图形成轴对称的定义,即看两个图形能否沿一条直线折叠后重合;若重合,则两个图形关于这条直线成轴对称,否则不成轴对称.
四、典型例题
解:如图所示;
【当堂检测】
1. 下面的图形是轴对称图形吗?如果是,你能指出它的对称轴吗?
解:图 1、2 是轴对称图形,它们的对称轴如图所示;图 3 不是.
图 1
图 3
图 2
四、典型例题
(二)平移的概念及特征
解:详见右图动画;
例 2:如图,在方格纸中,按要求做出平移后的图形;
(1)将右图中图形向上移动 3 格;
(2)将移动后的图形再向右移动 2 格;
注:平移后图形的形状和大小均不变.
【当堂检测】
2. 如图所示,下列四组图形中,哪一组的两个图形仅经过平移其中一个就能得到另一个,这组图形是( )
D
A B C D
(三)旋转及旋转对称图形
四、典型例题
例 3:如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,四边形的四个顶点都在格点上(每个小方格的顶点叫格点).请你画出如图四边形绕 点 O 逆时针旋转 90°后的图形.
O
解:详见右图动画;
注:旋转后对应点到旋转中心的距离相等.
3. 如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是 ( )
A. 72° B. 108° C. 144° D. 216°
B
【当堂检测】
例 4:如图所示四边形 A B C D 是四边形 ABCD 绕点 O 顺时针旋转 180°后形成的图形;请你指出图中所有相等的线段;
(四)中心对称
四、典型例题
A
B
D
C
O
B′
A′
D′
C′
解:图中相等的线段有:
AB = A B 、BC = B C 、CD = C D 、DA = D A ;
AO = A O 、BO = B O 、CO = C O 、DO = D O .
分析:根据中心对称图形的性质解答即可;
4. 下列图形是轴对称图形也是中心对称图形的是 ( )
B
【当堂检测】
例 5:如图,△ABC ≌ △EDB,AC = 6,AB = 8,求 AE = ?
(五)图形的全等
四、典型例题
A
B
E
D
C
分析:根据全等三角形对应边、角都相等,再结合已知求解即可;
又AB = AE + EB = 8;
解: 已知△ABC≌△DEF,
即 AC = EB = 6;
则 AE = AB – EB = 8 – 6 = 2;
故 AE = 2 .
【当堂检测】
5. 下列说法中正确的个数为 ( )
(1)所有的等边三角形都全等;
(2)两个三角形全等,它们的最大边是对应边;
(3)两个三角形全等,它们的对应角相等;
(4)对应角相等的三角形是全等三角形.
A. 1 B. 2 C. 3 D. 4
B
五、课堂总结
图形间的变换关系
轴对称
连接对应点的线段被对称轴垂直平分
平移
连接对应点的线段平行(或在同一条直线上)且相等;对应点线段平行(或在同一条直线上)且相等
旋转
对应点到旋转中心的距离相等;
每一个点都绕旋转中心按同一方向旋转了相同的角度
旋转对称
中心对称
在轴对称、平移、旋转等图形变换下,线段的长度、角的大小不变,变换前后两个图像是全等图形
全等多边形
全等多边形对应边、角分别相等;反之,可做判定.
复习课
第十章 轴对称、平移与旋转
一、学习目标
1.理解图形经过轴对称、平移、旋转后能得到一个与原图形全等的图形;
2.会画简单图形经过轴对称、平移、旋转后的图形;
3.会用轴对称、平移、旋转、全等的性质解决简单的数学问题.
二、知识结构
回顾:本章我们学了哪些内容?
图形间的变换关系
轴对称
连接对应点的线段被对称轴垂直平分
平移
连接对应点的线段平行(或在同一条直线上)且相等;对应点线段平行(或在同一条直线上)且相等
旋转
对应点到旋转中心的距离相等;
每一个点都绕旋转中心按同一方向旋转了相同的角度
旋转对称
中心对称
在轴对称、平移、旋转等图形变换下,线段的长度、角的大小不变,变换前后两个图像是全等图形
全等多边形
全等多边形对应边、角分别相等;反之,可做判定.
一、轴对称
三、知识回顾
1. 轴对称图形:把一个图形沿某条直线对折,对折后两部分能完全重合,这个图形就是轴对称图形,这条直线即为这个图形的对称轴;
2. 轴对称:一个图形沿一条直线翻折,如果它能够与另一个图形重合,那么就说这两个图形成轴对称,这条直线就是对称轴,两个图形中的对应点叫做对称点.
3. 轴对称图形的性质:轴对称图形(或成轴对称的两个图形)的对应线段相等,对应角相等;
4. 线段的垂直平分线:垂直并且平分一条线段的直线叫做这条线段的垂直平分线(或中垂线).
三、知识回顾
1. 平移:由移动的方向和距离所决定;
2. 平移的特征:平移后图形与原来图形的对应线段平行(或在同一直线上),并且相等;对应角相等,图形的形状与大小不变;
平移后对应点所连的线段平行 ( 或在同一直线上 ) 并且相等.
二、平移
三、知识回顾
1. 旋转:图形的旋转由旋转中心、旋转角度和旋转方向所决定;
2. 旋转的特征:图形中每一点都绕着旋转中心按同一方向旋转了同样大小的角度,对应点到旋转中心的距离相等,对应线段相等,图形的形状与大小不变.
三、旋转
三、知识回顾
3. 旋转对称图形:旋转一定角度后能与自身重合的图形叫做旋转对称图形;
4. 中心对称图形:一个图形绕着中心旋转 180 度后能与自身重合,我们把这种图形叫做中心对称图形.
三、知识回顾
5. 中心对称的性质:在成中心对称的两个图形中,连结对称点的线段都经过 对称中心,并且被对称中心 平分;
反过来,如果两个图形的所有对应点连成的线段都经过某一点,并且被该点 平分,那么这两个图形关于这一点成 中心对称.
四、全等
三、知识回顾
1. 全等多边形的性质:全等多边形的对应边、对应角分别相等;
2. 全等多边形的判定:如果两个多边形的边、角分别对应相等,那么这两个多边形全等.
(一)轴对称与轴对称图形
四、典型例题
例 1:观察图 ① ~ ④ 中的左右两个图形,它们是否成轴对称?如果是,请画出其对称轴.
分析:图 ① ② ③ 中的两个图形成轴对称;
图 ④ 中的两个图形不成轴对称;
图 ① ② ③ 中的对称轴如下图所示(下接).
注意:判断两个图形是否成轴对称,关键是理解、应用两个图形成轴对称的定义,即看两个图形能否沿一条直线折叠后重合;若重合,则两个图形关于这条直线成轴对称,否则不成轴对称.
四、典型例题
解:如图所示;
【当堂检测】
1. 下面的图形是轴对称图形吗?如果是,你能指出它的对称轴吗?
解:图 1、2 是轴对称图形,它们的对称轴如图所示;图 3 不是.
图 1
图 3
图 2
四、典型例题
(二)平移的概念及特征
解:详见右图动画;
例 2:如图,在方格纸中,按要求做出平移后的图形;
(1)将右图中图形向上移动 3 格;
(2)将移动后的图形再向右移动 2 格;
注:平移后图形的形状和大小均不变.
【当堂检测】
2. 如图所示,下列四组图形中,哪一组的两个图形仅经过平移其中一个就能得到另一个,这组图形是( )
D
A B C D
(三)旋转及旋转对称图形
四、典型例题
例 3:如图所示的方格纸中,每个小方格都是边长为1个单位的正方形,四边形的四个顶点都在格点上(每个小方格的顶点叫格点).请你画出如图四边形绕 点 O 逆时针旋转 90°后的图形.
O
解:详见右图动画;
注:旋转后对应点到旋转中心的距离相等.
3. 如图,该图形围绕自己的旋转中心,按下列角度旋转后,不能与其自身重合的是 ( )
A. 72° B. 108° C. 144° D. 216°
B
【当堂检测】
例 4:如图所示四边形 A B C D 是四边形 ABCD 绕点 O 顺时针旋转 180°后形成的图形;请你指出图中所有相等的线段;
(四)中心对称
四、典型例题
A
B
D
C
O
B′
A′
D′
C′
解:图中相等的线段有:
AB = A B 、BC = B C 、CD = C D 、DA = D A ;
AO = A O 、BO = B O 、CO = C O 、DO = D O .
分析:根据中心对称图形的性质解答即可;
4. 下列图形是轴对称图形也是中心对称图形的是 ( )
B
【当堂检测】
例 5:如图,△ABC ≌ △EDB,AC = 6,AB = 8,求 AE = ?
(五)图形的全等
四、典型例题
A
B
E
D
C
分析:根据全等三角形对应边、角都相等,再结合已知求解即可;
又AB = AE + EB = 8;
解: 已知△ABC≌△DEF,
即 AC = EB = 6;
则 AE = AB – EB = 8 – 6 = 2;
故 AE = 2 .
【当堂检测】
5. 下列说法中正确的个数为 ( )
(1)所有的等边三角形都全等;
(2)两个三角形全等,它们的最大边是对应边;
(3)两个三角形全等,它们的对应角相等;
(4)对应角相等的三角形是全等三角形.
A. 1 B. 2 C. 3 D. 4
B
五、课堂总结
图形间的变换关系
轴对称
连接对应点的线段被对称轴垂直平分
平移
连接对应点的线段平行(或在同一条直线上)且相等;对应点线段平行(或在同一条直线上)且相等
旋转
对应点到旋转中心的距离相等;
每一个点都绕旋转中心按同一方向旋转了相同的角度
旋转对称
中心对称
在轴对称、平移、旋转等图形变换下,线段的长度、角的大小不变,变换前后两个图像是全等图形
全等多边形
全等多边形对应边、角分别相等;反之,可做判定.
