17.4 一元二次方程的根与系数的关系 第2课时 课件(共14张PPT) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 17.4 一元二次方程的根与系数的关系 第2课时 课件(共14张PPT) 2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 663.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 08:47:19 | ||
图片预览






文档简介
(共14张PPT)
17.4 一元二次方程的根与系数的关系
第2课时
第十七章 一元二次方程
一、学习目标
1.能将一元二次方程中两根的其他运算关系转化为两根之和与两根之积之间的运算
2.通过利用一元二次方程根与系数的关系求代数式的值,进一步掌握“整体”代入法
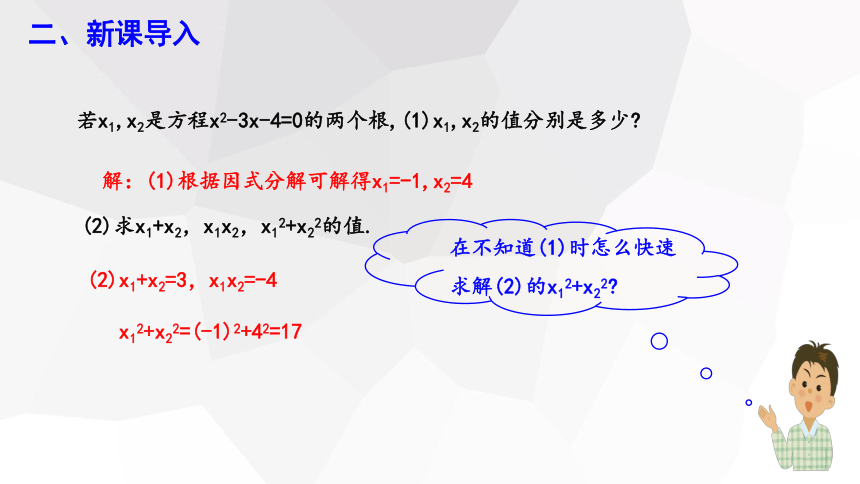
二、新课导入
若x1,x2是方程x2-3x-4=0的两个根,(1)x1,x2的值分别是多少
解:(1)根据因式分解可解得x1=-1,x2=4
在不知道(1)时怎么快速求解(2)的x12+x22
(2)求x1+x2,x1x2,x12+x22的值.
(2)x1+x2=3,x1x2=-4
x12+x22=(-1)2+42=17
例1.已知x1、x2是方程2x2-5x+1=0的两个实数根,求下列各式的值:
(1)x1+x2;(2)x1x2;(3)(x1+1)(x2+1);(4)x12+x22;(5)
提示:(3)(4)(5)转化为两根之积或两根之和求解
三、典型例题
解: =b2-4ac=(-5)2-4×2×1=17>0
故方程有两个不相等根
∴(1)x1+x2=2.5 ,(2)x1x2=0.5
(3)(x1+1)(x2+1)=x1x2+x1+x2+1
=2.5+0.5+1=4
例1.已知x1、x2是方程2x2-5x+1=0的两个实数根,求下列各式的值:
(4)x12+x22 (5)
三、典型例题
(4)x12+x22=x12+2x1x2+x22-2x1x2
=(x1+x2)2-2x1x2
=2.52-2×0.5=5.25
思考:根据(4)(5)快速写出(x1-x2)2, 的值.
解: (x1-x2)2 =(x1+x2)2-4x1x2
=2.52-4×0.5=4.25
常见求值:
(1)(x1+1)(x2+1)=x1x2+x1+x2+1
(2)x12+x22=(x1+x2)2-2x1x2
(x1-x2)2=(x1+x2)2-4x1x2
(3)
三、典型例题
总结:
1.求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
2.进行方程根倒数计算时,要注意根是否为0.
三、典型例题
【当堂检测】
1.若方程x2+x-1=0的两根为m,n,那么下列说法不正确的是( )
A.m+n=-1 B.mn=-1
C. D.m2+n2=1
D
2.若m、n是一元二次方程3x2+2x-9=0的两根,则的 值是( )
A. B.
C. D.
C
【当堂检测】
3.已知x1、x2是方程4x2-7x+1=0的两个实数根,求下列各式的值:
(1)x1x22+x12x2;
(2)x12+x22.
解: =b2-4ac=(-7)2-4×4×1=33>0
故方程有两个不相等根
∴x1+x2= ,x1x2=
(1)x1x22+x12x2=x1x2(x1+x2)
(2)x12+x22=(x1+x2)2-2x1x2
例2.已知2m2-3m-2=0, 且m、n不等,
(1)求m+n,mn的值;
(2)求m2-n2+mn+3n的值.
解:(1) 去分母,得2n2-3n-2=0
根据根的定义可知:m、n是方程2x2-3x-2=0的两个根
∴m+n=1.5,mn=-1
分析:将n的方程转化为一元二次方程,对比m、n的两个方程,发现是同一方程的不同值的代入;
第(2)问的代数式转化成与m+n、mn的式子进行求值
三、典型例题
例2.已知2m2-3m-2=0, 且m、n不等,
(2)求m2-n2+mn+3n的值.
解:(2)由(1)可知:m、n是方程2x2-3x-2=0的两个根
则m2=1.5m+1,n2=1.5n+1
原式=1.5m+1-(1.5n+1)+mn+3n
=1.5(m+n)+mn
=1.5×1.5-1
=1.25
三、典型例题
【当堂检测】
4.设m、n是一元二次方程x2+x-3=0的两根,则m2-n+2019=( )
A.2023 B.2021
C.2020 D.2019
A
2020
5.若方程x2-x-2019=0的两根分别为α,β,则α2+β= .
6.已知互不相等的实数m、n,且满足m2 3m 5 0,n2 3n 5 0,则m3-2n2+mn-8m的值.
解:根据根的定义可知:m、n是方程x2+3x-5=0的两个根
∴m+n=-3,mn=-5
∵m2 3m 5 0,n2 3n 5 0
∴m2=5-3m,n2=5-3n
m3=m·m2=m(5-3m)
=5m-3m2
=5m-3(5-3m)
=14m-15
【当堂检测】
原式=14m-15-2(5-3n)+mn-8m
=6m+6n+mn-25
=6(m+n)+mn-25
=6×(-3)-5-25
=-48
四、课堂总结
1.求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
2.常见的根的求值:
(1)(x1+1)(x2+1)=x1x2+x1+x2+1
(2)x12+x22=(x1+x2)2-2x1x2
(x1-x2)2 =(x1+x2)2-4x1x2
(3)
17.4 一元二次方程的根与系数的关系
第2课时
第十七章 一元二次方程
一、学习目标
1.能将一元二次方程中两根的其他运算关系转化为两根之和与两根之积之间的运算
2.通过利用一元二次方程根与系数的关系求代数式的值,进一步掌握“整体”代入法
二、新课导入
若x1,x2是方程x2-3x-4=0的两个根,(1)x1,x2的值分别是多少
解:(1)根据因式分解可解得x1=-1,x2=4
在不知道(1)时怎么快速求解(2)的x12+x22
(2)求x1+x2,x1x2,x12+x22的值.
(2)x1+x2=3,x1x2=-4
x12+x22=(-1)2+42=17
例1.已知x1、x2是方程2x2-5x+1=0的两个实数根,求下列各式的值:
(1)x1+x2;(2)x1x2;(3)(x1+1)(x2+1);(4)x12+x22;(5)
提示:(3)(4)(5)转化为两根之积或两根之和求解
三、典型例题
解: =b2-4ac=(-5)2-4×2×1=17>0
故方程有两个不相等根
∴(1)x1+x2=2.5 ,(2)x1x2=0.5
(3)(x1+1)(x2+1)=x1x2+x1+x2+1
=2.5+0.5+1=4
例1.已知x1、x2是方程2x2-5x+1=0的两个实数根,求下列各式的值:
(4)x12+x22 (5)
三、典型例题
(4)x12+x22=x12+2x1x2+x22-2x1x2
=(x1+x2)2-2x1x2
=2.52-2×0.5=5.25
思考:根据(4)(5)快速写出(x1-x2)2, 的值.
解: (x1-x2)2 =(x1+x2)2-4x1x2
=2.52-4×0.5=4.25
常见求值:
(1)(x1+1)(x2+1)=x1x2+x1+x2+1
(2)x12+x22=(x1+x2)2-2x1x2
(x1-x2)2=(x1+x2)2-4x1x2
(3)
三、典型例题
总结:
1.求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
2.进行方程根倒数计算时,要注意根是否为0.
三、典型例题
【当堂检测】
1.若方程x2+x-1=0的两根为m,n,那么下列说法不正确的是( )
A.m+n=-1 B.mn=-1
C. D.m2+n2=1
D
2.若m、n是一元二次方程3x2+2x-9=0的两根,则的 值是( )
A. B.
C. D.
C
【当堂检测】
3.已知x1、x2是方程4x2-7x+1=0的两个实数根,求下列各式的值:
(1)x1x22+x12x2;
(2)x12+x22.
解: =b2-4ac=(-7)2-4×4×1=33>0
故方程有两个不相等根
∴x1+x2= ,x1x2=
(1)x1x22+x12x2=x1x2(x1+x2)
(2)x12+x22=(x1+x2)2-2x1x2
例2.已知2m2-3m-2=0, 且m、n不等,
(1)求m+n,mn的值;
(2)求m2-n2+mn+3n的值.
解:(1) 去分母,得2n2-3n-2=0
根据根的定义可知:m、n是方程2x2-3x-2=0的两个根
∴m+n=1.5,mn=-1
分析:将n的方程转化为一元二次方程,对比m、n的两个方程,发现是同一方程的不同值的代入;
第(2)问的代数式转化成与m+n、mn的式子进行求值
三、典型例题
例2.已知2m2-3m-2=0, 且m、n不等,
(2)求m2-n2+mn+3n的值.
解:(2)由(1)可知:m、n是方程2x2-3x-2=0的两个根
则m2=1.5m+1,n2=1.5n+1
原式=1.5m+1-(1.5n+1)+mn+3n
=1.5(m+n)+mn
=1.5×1.5-1
=1.25
三、典型例题
【当堂检测】
4.设m、n是一元二次方程x2+x-3=0的两根,则m2-n+2019=( )
A.2023 B.2021
C.2020 D.2019
A
2020
5.若方程x2-x-2019=0的两根分别为α,β,则α2+β= .
6.已知互不相等的实数m、n,且满足m2 3m 5 0,n2 3n 5 0,则m3-2n2+mn-8m的值.
解:根据根的定义可知:m、n是方程x2+3x-5=0的两个根
∴m+n=-3,mn=-5
∵m2 3m 5 0,n2 3n 5 0
∴m2=5-3m,n2=5-3n
m3=m·m2=m(5-3m)
=5m-3m2
=5m-3(5-3m)
=14m-15
【当堂检测】
原式=14m-15-2(5-3n)+mn-8m
=6m+6n+mn-25
=6(m+n)+mn-25
=6×(-3)-5-25
=-48
四、课堂总结
1.求与方程的根有关的代数式的值时,一般先将所求的代数式化成含两根之和,两根之积的形式,再整体代入.
2.常见的根的求值:
(1)(x1+1)(x2+1)=x1x2+x1+x2+1
(2)x12+x22=(x1+x2)2-2x1x2
(x1-x2)2 =(x1+x2)2-4x1x2
(3)
