17.4 一元二次方程的根与系数的关系 第1课时 课件(共15张PPT) 2023-2024学年初中数学沪科版八年级下册
文档属性
| 名称 | 17.4 一元二次方程的根与系数的关系 第1课时 课件(共15张PPT) 2023-2024学年初中数学沪科版八年级下册 |

|
|
| 格式 | pptx | ||
| 文件大小 | 184.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-02-21 00:00:00 | ||
图片预览






文档简介
(共15张PPT)
17.4 一元二次方程的根与系数的关系
第1课时
第十七章 一元二次方程
一、学习目标
1.熟知一元二次方程的根与系数的关系
2.会运用根与系数的关系解决有关问题(重点)
二、新课导入
一元二次方程ax2+bx+c=0(a≠0)通过什么来判断方程根的情况?
判别式 ( =b2-4ac), >0,方程有两个不等实根;
=0,方程有两个相等实根;
<0,方程没有实数根.
思考:若方程有实数根x1,x2,写出x1,x2的值,那么x1+x2,x1x2和a、b、c有什么关系?
三、概念剖析
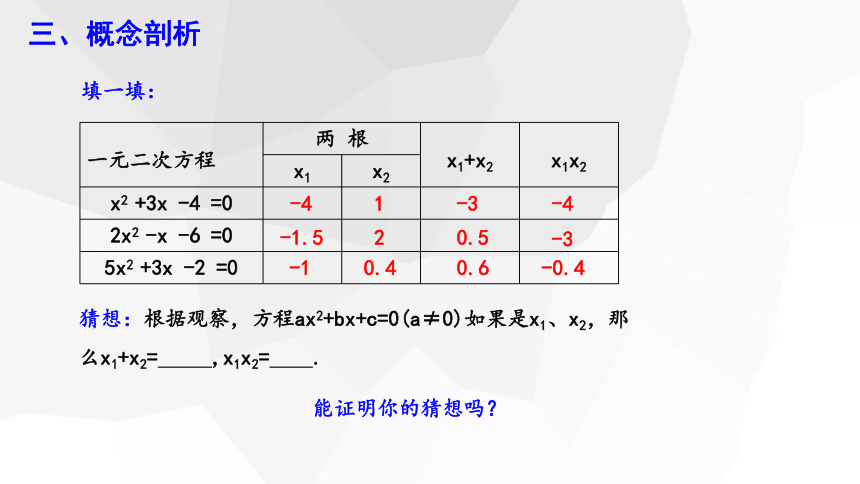
填一填:
一元二次方程 两 根 x1+x2 x1x2
x1 x2
x2 +3x -4 =0
2x2 -x -6 =0
5x2 +3x -2 =0
-4
1
-3
-4
-1.5
2
0.5
-3
-1
0.4
0.6
-0.4
猜想:根据观察,方程ax2+bx+c=0(a≠0)如果是x1、x2,那么x1+x2= ,x1x2= .
能证明你的猜想吗?
三、概念剖析
韦达定理:
如果ax2+bx+c=0(a≠0)的两个根分别是x1、x2,那么x1+x2= ,
x1x2=
证一证:
x1+x2
x1·x2
例1.小明某天的作业如下:
(1)x2+2x-12=8x+3 ,则x1+x2=(-2) ,x1x2=(-12)
(2)x2-2x+3=0,则x1+x2=(2) ,x1x2=(3)
(3)3x2+7x-9=0,则x1+x2=(7) ,x1x2=(-9)
小明的答案是否正确?若错误,写出正确答案.
提示:对于ax2+bx+c=0 (a 0, ≥0),x1+x2= ,x1x2=
四、典型例题
解:(1)方程化为一般式:x2-6x-15=0
=b2-4ac=(-6)2-4×1×(-15)=96>0
故方程有两个不相等根
∴x1+x2=6 ,x1x2=-15
∴(1)答案错误
x1+x2=6 ,x1x2=-15
(2)x2-2x+3=0,则x1+x2=(2) ,x1x2=(3)
四、典型例题
(2) =b2-4ac=(-2)2-4×1×3=-8<0
故方程没有实数根
∴不存在x1+x2,x1x2
∴(2)答案错误
(3) =b2-4ac=72-4×2×(-8)=113>0
故方程有两个不相等根
∴x1+x2=-3.5,x1x2=-4
∴(3)答案错误
(3)2x2+7x-8=0,则x1+x2=(3.5) ,x1x2=(-4)
不存在x1+x2,x1x2
-3.5
注意事项:
(1)方程要化为一般形式;
(2) ≥0;
(3)x1+x2=
【当堂检测】
1.在下列方程中,以3,-4为根的一元二次方程是( )
A.x2-x-12=0 B.x2+x-12=0
C.x2-x+12=0 D.x2+x+12=0
B
【当堂检测】
2.判定下列各方程后面括号内的两个数是不是它的两个根.
(1)x2+5x+4=0(1,4);
(2)x2-6x-7=0(-1,7);
(3)2x2-3x+1=0(0.5,1);
(4)3x2+5x-2=0( ,2);
(1)x2-8x+11=0(3,5);
不是
是
是
不是
不是
例2.一元二次方程x2 (m 1)x 2m 1 0,
(1)求m满足什么条件时,方程的两根互为相反数?
解:(1)a=1,b= (m 1),c=2m 1
△=b2-4ac=[ (m 1)]2-4×1×(2m 1)=m2 6m 5
∵两根互为相反数
∴两根之和=m 1=0,
解得m 1,
此时△=m2 6m 5=(-1)2 6×(-1) 5=12>0,方程有两个不等根
∴m 1时,方程的两根互为相反数.
四、典型例题
两数之和为0
方程形如ax2+bx+c=0 (a 0, ≥0),若两根互为相反数,则b=0
例2.一元二次方程x2 (m 1)x 2m 1 0,
(2)求m满足什么条件时,方程的两根互为倒数?
(2)∵两根互为倒数
∴两根之积=2m 1=1
解得m 1
此时△=m2 6m 5=12 6×1 5=0,方程有两个相等的根
∴m 1时,方程的两根互为倒数.
四、典型例题
两数之积为1
方程形如ax2+bx+c=0 (a 0, ≥0),若两根互为倒数,则a c
例2.一元二次方程x2 (m 1)x 2m 1 0,
(3)求m满足什么条件时,方程的一根为零?
(3)∵方程一根为0
∴两根之积=2m 1=0
解得m 0.5
此时△=m2 6m 5=(0.5)2 6×0.5 5=2.25>0,方程有两个不等根
∴m 0.5时,方程的一根为零
四、典型例题
任何一个数与0相乘结果为0
两根之积为0
方程形如ax2+bx+c=0 (a 0, ≥0),若一根为0,则c=0
【当堂检测】
3.已知关于x的一元二次方程x2-(k+1)x-6=0的一个根是2,则此方程的另一个根和k的值分别是( )
A.3和2 B.3和-2
C.-3和-2 D.2和3
4.若x的一元二次方程x2-(2m-1)x-6=0的两根互为相反数,则k .
C
0.5
5.已知关于x的一元二次方程x2-2x+m=0有两个不等实根,
(1)求m的范围;
(2)若两个实数根为x1,x2,且x1+2x2=6,求m的值.
解:(1)a=1,b=-2,c=m
△=b2-4ac=(-2)2-4×1×m=4-4m
依题有:△>0,即4-4m>0
解得m<1
x1+x2=2
x1+2x2=6
(2)根据韦达定理可知:x1+x2=2,x1x2=m
∵
解得x1=-2,x2=4
∴m=x1x2=(-2)×4=-8
-8<1,故m的值为-8
【当堂检测】
五、课堂总结
1.计算根与系数的关系时注意事项:
(1)方程要化为一般形式;
(2) ≥0;
2.若ax2+bx+c=0 (a 0, 0),x1+x2= ,x1x2=
(1)若两根互为相反数,则b=0;
(2)若两根互为倒数,则a=c;
(3)若一根为0,则c=0.
17.4 一元二次方程的根与系数的关系
第1课时
第十七章 一元二次方程
一、学习目标
1.熟知一元二次方程的根与系数的关系
2.会运用根与系数的关系解决有关问题(重点)
二、新课导入
一元二次方程ax2+bx+c=0(a≠0)通过什么来判断方程根的情况?
判别式 ( =b2-4ac), >0,方程有两个不等实根;
=0,方程有两个相等实根;
<0,方程没有实数根.
思考:若方程有实数根x1,x2,写出x1,x2的值,那么x1+x2,x1x2和a、b、c有什么关系?
三、概念剖析
填一填:
一元二次方程 两 根 x1+x2 x1x2
x1 x2
x2 +3x -4 =0
2x2 -x -6 =0
5x2 +3x -2 =0
-4
1
-3
-4
-1.5
2
0.5
-3
-1
0.4
0.6
-0.4
猜想:根据观察,方程ax2+bx+c=0(a≠0)如果是x1、x2,那么x1+x2= ,x1x2= .
能证明你的猜想吗?
三、概念剖析
韦达定理:
如果ax2+bx+c=0(a≠0)的两个根分别是x1、x2,那么x1+x2= ,
x1x2=
证一证:
x1+x2
x1·x2
例1.小明某天的作业如下:
(1)x2+2x-12=8x+3 ,则x1+x2=(-2) ,x1x2=(-12)
(2)x2-2x+3=0,则x1+x2=(2) ,x1x2=(3)
(3)3x2+7x-9=0,则x1+x2=(7) ,x1x2=(-9)
小明的答案是否正确?若错误,写出正确答案.
提示:对于ax2+bx+c=0 (a 0, ≥0),x1+x2= ,x1x2=
四、典型例题
解:(1)方程化为一般式:x2-6x-15=0
=b2-4ac=(-6)2-4×1×(-15)=96>0
故方程有两个不相等根
∴x1+x2=6 ,x1x2=-15
∴(1)答案错误
x1+x2=6 ,x1x2=-15
(2)x2-2x+3=0,则x1+x2=(2) ,x1x2=(3)
四、典型例题
(2) =b2-4ac=(-2)2-4×1×3=-8<0
故方程没有实数根
∴不存在x1+x2,x1x2
∴(2)答案错误
(3) =b2-4ac=72-4×2×(-8)=113>0
故方程有两个不相等根
∴x1+x2=-3.5,x1x2=-4
∴(3)答案错误
(3)2x2+7x-8=0,则x1+x2=(3.5) ,x1x2=(-4)
不存在x1+x2,x1x2
-3.5
注意事项:
(1)方程要化为一般形式;
(2) ≥0;
(3)x1+x2=
【当堂检测】
1.在下列方程中,以3,-4为根的一元二次方程是( )
A.x2-x-12=0 B.x2+x-12=0
C.x2-x+12=0 D.x2+x+12=0
B
【当堂检测】
2.判定下列各方程后面括号内的两个数是不是它的两个根.
(1)x2+5x+4=0(1,4);
(2)x2-6x-7=0(-1,7);
(3)2x2-3x+1=0(0.5,1);
(4)3x2+5x-2=0( ,2);
(1)x2-8x+11=0(3,5);
不是
是
是
不是
不是
例2.一元二次方程x2 (m 1)x 2m 1 0,
(1)求m满足什么条件时,方程的两根互为相反数?
解:(1)a=1,b= (m 1),c=2m 1
△=b2-4ac=[ (m 1)]2-4×1×(2m 1)=m2 6m 5
∵两根互为相反数
∴两根之和=m 1=0,
解得m 1,
此时△=m2 6m 5=(-1)2 6×(-1) 5=12>0,方程有两个不等根
∴m 1时,方程的两根互为相反数.
四、典型例题
两数之和为0
方程形如ax2+bx+c=0 (a 0, ≥0),若两根互为相反数,则b=0
例2.一元二次方程x2 (m 1)x 2m 1 0,
(2)求m满足什么条件时,方程的两根互为倒数?
(2)∵两根互为倒数
∴两根之积=2m 1=1
解得m 1
此时△=m2 6m 5=12 6×1 5=0,方程有两个相等的根
∴m 1时,方程的两根互为倒数.
四、典型例题
两数之积为1
方程形如ax2+bx+c=0 (a 0, ≥0),若两根互为倒数,则a c
例2.一元二次方程x2 (m 1)x 2m 1 0,
(3)求m满足什么条件时,方程的一根为零?
(3)∵方程一根为0
∴两根之积=2m 1=0
解得m 0.5
此时△=m2 6m 5=(0.5)2 6×0.5 5=2.25>0,方程有两个不等根
∴m 0.5时,方程的一根为零
四、典型例题
任何一个数与0相乘结果为0
两根之积为0
方程形如ax2+bx+c=0 (a 0, ≥0),若一根为0,则c=0
【当堂检测】
3.已知关于x的一元二次方程x2-(k+1)x-6=0的一个根是2,则此方程的另一个根和k的值分别是( )
A.3和2 B.3和-2
C.-3和-2 D.2和3
4.若x的一元二次方程x2-(2m-1)x-6=0的两根互为相反数,则k .
C
0.5
5.已知关于x的一元二次方程x2-2x+m=0有两个不等实根,
(1)求m的范围;
(2)若两个实数根为x1,x2,且x1+2x2=6,求m的值.
解:(1)a=1,b=-2,c=m
△=b2-4ac=(-2)2-4×1×m=4-4m
依题有:△>0,即4-4m>0
解得m<1
x1+x2=2
x1+2x2=6
(2)根据韦达定理可知:x1+x2=2,x1x2=m
∵
解得x1=-2,x2=4
∴m=x1x2=(-2)×4=-8
-8<1,故m的值为-8
【当堂检测】
五、课堂总结
1.计算根与系数的关系时注意事项:
(1)方程要化为一般形式;
(2) ≥0;
2.若ax2+bx+c=0 (a 0, 0),x1+x2= ,x1x2=
(1)若两根互为相反数,则b=0;
(2)若两根互为倒数,则a=c;
(3)若一根为0,则c=0.
